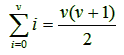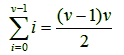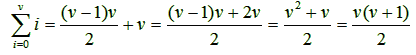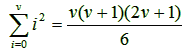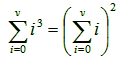 |
Automata – Formal Languages – ComputabilityCLASS NOTES FOR COURSE C5 OF I.C.S.
|
|
Prerequisites and Contents of this Course
Prerequisites
This course assumes knowledge of the fundamental notions of computers (course C1), but also some mathematical background, since it lies in the intersection of the domains of mathematics and computers. Specifically, it is required to have knowledge, prior training, and especially fluency in mathematical proofs. In particular, the proving method of mathematical induction is reviewed in the introductory section (because it is used in many theorems), but the reader should not expect to be trained in mathematical induction by this course; one must have this skill, which is acquired in course M1. Naturally, the mathematical background cannot be acquired merely by course M1, but by the training in a multitude of mathematical courses; e.g., in Logic (M2), Set Theory (M7), Number Theory (M8), and more.
Contents and Aim
The present course forms the “core” of the domain of knowledge known as “computer science”; i.e., one cannot claim to have studied computer science without having acquired in-depth knowledge of all the notions included in this course. It is concerned with the notion of computability and with the various formal systems through which we can define computational machines. Two kinds of such formal systems are: 1. the finite automata, and 2. the formal languages. It examines the equivalence between some categories of automata and languages, and thus constructs, step by step, the essence of the entire theory of computability, which is the Chomsky hierarchy.
Among the aims of this course are: understanding the notion of computability; when a problem is characterized decidable, and when undecidable; understanding the four classes of formal systems that form the Chomsky hierarchy; and acquiring an in-depth knowledge of the essence of the notion of “computer”.
We shall learn the characteristics that a device must have so that it can be said to “compute” something. Four such categories of devices will be discovered, each “computationally more powerful” (computing more functions) than the previous category, and without any other type of device being able to “fit in between” those four. The fourth of those categories of devices, which is the Turing Machine, will turn out to be the most powerful computer that we have ever built. Every added feature to the basic Turing Machine will turn out to add no more power to it, in the sense that there will be no function that can be computed by the augmented device but cannot also be computed by the basic Turing Machine. Thus we shall conclude the so-called Church–Turing Thesis, which states that the Turing Machine (or any equivalent device) is the most powerful computer that we can ever dream of. And, because the neurons of the brain can be rather easily modeled by computing devices, the Church–Turing Thesis has implications about human cognition, suggesting that modern computers might be equivalent in computational power to the human brain. These and several more, interesting results are included in the material of this course.
These notes were based on the books listed in the bibliography.
1. Introductory Notions
In this section we shall make a brief review of the fundamental notions that the theory of computability uses and on which it rests.
1.1 Symbols, alphabets, strings, and languages
Just as geometry starts with some notions that it considers as primary, without defining them (e.g., point, straight line), so the present theory rests on notions without definition, one of which is the notion of symbol.* To denote symbols, we shall be using letters, digits, etc., all belonging to an alphabet:
Definition: an alphabet is a finite set of symbols.
Examples of alphabets are: {a, b, c}, {0, 1}, {z, $, 8, -}, etc. Usually, to avoid confusion, we shall be using Roman letters or digits for the symbols of an alphabet. E.g., of the previous examples, {a, b, c} and {0, 1} are examples of alphabets that we shall be using often, since other symbols (such as +, *, etc.) will be used to denote operations between objects of this course. Greek letters, such as Σ, will be used to denote the entire alphabet; e.g., Σ = {a, b}.
Definition: a string is a sequence of symbols that belong to an alphabet.
Examples of strings are: babba, abba, aaaabbbb, constructed from the alphabet {a, b}, but also from {a, b, c}, etc. Also, the strings 1000, 1010101010, and 000001, are constructed from an alphabet that contains at least the symbols 0 and 1; and so on.
We accept the existence of the empty string, which will be denoted by the Greek letter epsilon: ε (lowercase and in italics).
We shall be using Roman letters in italics from the end of the alphabet (w, x, y, z) to denote strings in general. An exception will be, as just mentioned, the empty string ε.
Definition: the length of a string is the number of symbols that form the string. We shall be using the notation |w| for the length of string w.
E.g., |abba| equals 4, whereas |ε| = 0.
Definition: a prefix of a string w is any initial part of w· correspondingly, a suffix of w is any final part of w.
E.g., aaa is a prefix of aaaaab, whereas ab is a suffix of the same string. Clearly, ε is both prefix and suffix of every string. Also clearly, every string is prefix and suffix of itself.
Definition: a proper prefix, and similarly, a proper suffix of a string is any prefix of suffix, respectively, of it except itself.
Definition: the result of the operation of concatenation of two strings x and y is the string that results from simply juxtaposing the two strings (in that order): xy.
E.g., the concatenation of ab and ba is abba. The concatenation of 0101 and ε is 0101, which is also the concatenation of ε and 0101.
Clearly, the operation of concatenation is transitive, since (xy)z = x(yz). Thus, we shall write simply xyz meaning the concatenation of x, y, and z, since the priority by which the two concatenations are executed is inconsequential.
Definition: a formal language (which we shall usually call simply language) is a set of strings from the same alphabet.
Examples: the empty set Ø, as well as the set {ε}, are languages; the former has cardinality* 0, whereas the latter has cardinality 1. Let it be noted that a language is not assumed to be necessarily a finite set; it can also be (and usually is) infinite. For the following example of an infinite language we will need a definition:
Definition: a string is a palindrome if (and only if)* it can be read the same both left-to-right and right-to-left.
The set of all palindromes from an alphabet is an infinite language. E.g., the set of all palindromes from the alphabet Σ = {a, b} is the language: {ε, a, b, aa, bb, aaa, bbb, aba, bab, ...}. We shall be using capital Roman letters to denote languages, e.g.: L, G, etc.
Another infinite language is the set of all strings from an alphabet Σ. We shall be using the notation Σ* for that language. (Note: Σ is an alphabet, whereas Σ* is a language.) In general, the symbol * will be used for an operation on languages, called “Kleene closure” *:
Definition: the Kleene closure of a language L, which we denote by L*, is the language that results from the concatenation of any number of strings of L.
E.g., if L = {aa, ba}, then L* = {ε, aa, ba, aaaa, aaba, baaa, baba, ...}. Observe that Kleene closure is always an infinite language.
The Kleene closure can be similarly defined over an alphabet Σ: it is the language that results from the concatenation of any number of symbols from Σ.
This operation is called a “closure” because its repeated application does not yield a different result: (L*)* = L*. In other words, the resulting set is “closed” (in terms of new elements) with one and only application of the operation.
Exercise 1.1.1: Write 8 elements of the closure L*, where L is the language {ε, a, b, ba}. Can ε be one of those elements? Can εε be one of them?
1.2 Graphs and Trees
For the representation of finite automata, which we shall meet in the following section, we shall use the graph structure.
Definition: a graph G is an ordered pair of finite sets (V, E), where V is called the set of vertices of the graph, and E, which is called the set of edges of the graph, is a set of (not necessarily ordered) pairs of vertices from V (or otherwise: E is a binary relation in V).
Example:
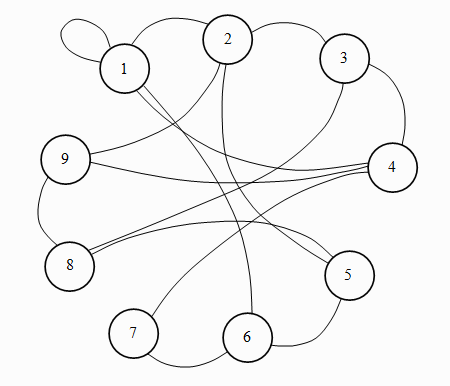
Fig. 1.1: a graph
The above graph G = (V, E) has V = {1, 2, ..., 9} and Ε = {(i, j) | i + j = prime number}.
Definition: a directed graph is a graph in which the set E of edges is a set of ordered pairs of vertices from V.
Consequently, in a directed graph, the “from” and the “to” of an edge (from which vertex it emanates and to which one it points) is important. An example of a directed graph follows.
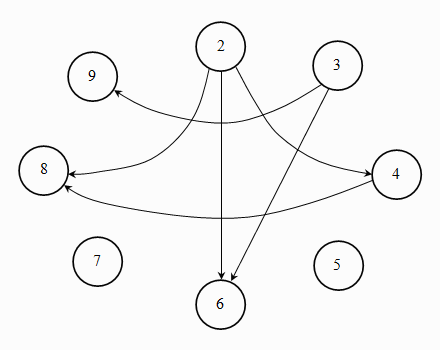
Fig. 1.2: a directed graph
The above graph G = (V, E) has V = {2, 3, ..., 9} and Ε = {(i, j) | i < j and i divides j}.
Definition:
a
path
in a graph G = (V, E)
is a sequence of vertices v1,
v2, ..., vk
from V,
with
k > 0, such that
edge (vi,
vi+1)
exists
![]() i,
i,
1
![]() i < k.
The length of such a path is
k
– 1.
i < k.
The length of such a path is
k
– 1.
As we see from the previous example, a graph does not necessarily form “one piece”. When the graph is in “one piece” it is called “connected”. However, for all the examples of finite automata we shall use directed graphs none of which will come in two or more pieces. For this reason we do not need to define connected graphs formally.
Exercise 1.2.1: Draw graph G = (V, E) where V = {2, 3, ..., 9} and Ε = {(i, j) | i & j are coprime}. (Two integers are called “coprime” when they have no other common divisor except 1.) Is G directed or not? Is there a path from 2 to 8 in G?
Definition: given an edge (u, v) of a directed graph G, the vertex u is called a predecessor of v, whereas v is called a successor of u.
Definition: a tree is a directed graph in which the following hold:
-
There is one vertex, called the root, which has no predecessor, and from which there is a path to every vertex.
-
Every vertex except the root has exactly one predecessor.
-
The successors of each vertex are ordered.
The order of successors of a vertex in a tree (condition 3) allows us to draw them from left to right when we depict a tree visually. In depictions, trees will be drawn “upside down”, with the root at the top and the successors of each vertex hanging below it, ordered.* In the diagram that follows, an example of a tree is given in which the label of each vertex is the product of the labels of its successors.
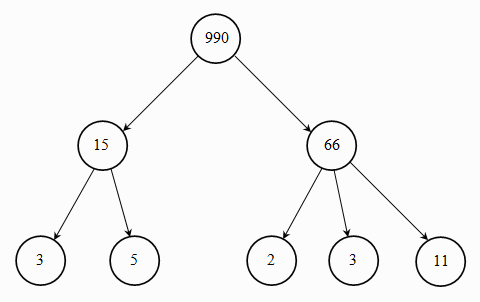
Fig. 1.3: a tree
The above tree could be defined as a factorization of integer 990 in prime numbers. We shall use trees primarily to represent grammars (“context free” and “context sensitive”), in later sections. When dealing with trees, we make use of a more specialized terminology:
Definition: in a tree, the predecessor is called a parent, whereas the successors are called children.
For instance, in the tree of the previous example, the parent of the vertex labeled “5” is the vertex “15”, whereas the children of “990” are “15” and “66”.
1.3 Proofs by Induction
Here we shall make a brief review of the proving method of mathematical induction. Suppose we have a proposition P(ν), which depends on a natural number ν, and takes on values “true” or “false” (in other words, it is a predicate). The principle of mathematical induction says that to prove that P(ν) is true, it suffices to show that:
-
P(0), and
-
P(ν – 1) → P(ν)
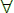 ν
ν
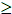 1.
1.
Condition (1), above, is called inductive basis, whereas condition (2) is called inductive step. P(ν – 1) in (2) is called inductive hypothesis.
Example: suppose that proposition P(ν) that we want to prove is the following equality:
We prove P(ν) by induction. The induction basis, P(0), holds in a trivial way: 0 = 0(0+1)/2, i.e., 0 = 0. For the inductive step now: from the inductive hypothesis P(ν – 1) we have that:
![]() ν
ν
![]() 1,
and we want to conclude P(ν). Adding ν on both sides of P(ν
– 1), we get:
1,
and we want to conclude P(ν). Adding ν on both sides of P(ν
– 1), we get:
We observe that the left and right side of the above multi-step equality is precisely P(ν). Therefore P(ν) is true. ▓
(In the above proof we make use of the symbol ▓ which we shall use to denote the “q.e.d.” at the end of every proof.)
Exercise 1.3.1: Prove by induction on ν the equality:
Exercise 1.3.2: Prove by induction on ν the equality:
Let us see an application of induction not on equalities but on the length of strings, which is the kind of induction that we shall meet more often in this course.
As mentioned earlier, a definition for palindrome says that it is the string that can be read the same both left-to-right and right-to-left. E.g., the following strings are palindromes:
00101aba10100
madaminedenimadam
Now we want to prove the following:
Theorem: a string x is a palindrome if and only if it is a member of the smallest set P that:
-
includes ε,
-
includes every symbol a of the alphabet, and
-
includes all strings of the form aya, where a is any symbol of the alphabet and y
 P.
P.
|
Proof. The direction “if” of the
theorem is rather obvious, because if x
Suppose that string x is a
palindrome, that is, it is read the same in both directions. We’ll prove
the theorem by induction on the length of x. If |x|
|
2. Finite Automata
2.1 Deterministic Finite Automata
A Finite Automaton (FA) is a mathematical model of a system (which can be physical — we’ll see examples immediately below) that can be in a state or states at any moment, having processed some input data. Optionally, the FA may accept the input data having arrived at a final state; otherwise, if the input data ended and the FA is not in a final state, it will reject the input data. Also optionally, it may have created some output data during its functioning.
A simple example of an FA is an old-fashioned elevator (electrical, not electronic). The state at which an electrical elevator exists is the floor at which it has stopped, waiting for passengers. (For the sake of simplicity, we ignore the time that lapses while the elevator moves from floor to floor.) The input data that the elevator has processed are the calling buttons that were pressed, either from the various floors, or from inside the cabin. The electrical elevator has no memory, therefore each button that calls it or directs it to go to some floor is the “next input datum” if the elevator is not moving. (If it is moving, button presses are ignored in such elevators.) An immediate processing of that datum takes place, i.e., the elevator changes state, moving to the floor that it must serve. Note that the elevator (of any type) is a special kind of automaton, because it doesn’t have a final state (it never ceases functioning; never does it come to a state that corresponds to the idea: “this is the end, I will process no more input”).
The following graph depicts an FA that models such an elevator for three floors:

Fig. 2.1.1: FA for an elevator that serves three floors
In the diagram, above, the FA shown by the graph models an elevator for three floors. States q0, q1, and q2 mean that the elevator is waiting at the ground floor, first floor, and second floor, respectively. The arrows that emanate from each state show in which state the automaton will end up being after pushing the button of the corresponding floor. E.g., when the elevator is at the ground floor (q0), pressing the ground floor button (0) has no effect, so the elevator remains at state q0. On the contrary, at state q0, pressing the first-floor button, the FA switches to state q1 (“waiting at the first floor”), whereas pressing the second-floor button switches to state q2 (“waiting at the second floor”). Buttons 0, 1, and 2 are the input data. Each state qi must respond to each input datum i, where i = 0, 1, 2, so that the elevator functions properly. Also, we see a convention that we make from now on in the graphs of all automata: the initial state (q0) will be distinguished from all the rest by the arrow that points to it, coming “from nowhere” (horizontal in the drawing).
The electronic elevator differs in an essential way from the electric one, because it passes from state to state in a different way: buttons pushed from inside the cabin take priority from buttons pushed at each floor. Also, it may “opt” to serve first the floor that is near the current one, rather than the one farther away. Thus, the electronic elevator works according to a “program”, the computational power of which exceeds that of FA’s. (It requires an automaton of higher computational power, such as those that we’ll meet in later sections.) For this reason, here we’ll confine ourselves to the example of the electric elevator.
Let’s modify slightly the notion of an elevator. Whereas normally the purpose of an elevator is to serve (indefinitely, without end) the passengers, suppose we now deal with an elevator of a special “purpose”, which is to reach the second floor; once there, it ceases functioning. Thus, we may claim that this elevator has a final state, q2, which will be denoted with a double circle, as in the following diagram:

Fig. 2.1.2: elevator FA with final state q2
In addition we may claim that, thanks to its final state, this automaton, starting from the initial state q0, accepts the sequence of input data (i.e. presses of buttons) 1010012, because after responding to that input it ends up at state q2, which is final. Thus, it accepts the string 1010012. In contrast, it rejects the string 01011, because that one does not lead the automaton to state q2. We note that it also accepts the string 00222, because an FA is not required to stop after reaching a final state; to determine the acceptance or rejection of input, what’s important is in which state the automaton is after processing the last input element.
Forgetting for a minute that the above automaton models an elevator, and seeing it somewhat abstractly, we may say that it accepts all strings that end in one or more 2’s, and rejects all the rest.
Therefore, we can view an automaton as a device that either accepts or rejects a string of input data.
Exercise 2.1.1: Construct the graph of an FA that accepts all strings (and only those strings) that consist of 0’s and 1’s and which have at least three successive 1’s.
Exercise 2.1.2: Construct the graph of an FA that accepts all strings (and only those strings) that consist of 0’s and 1’s and which have an even number of 0’s.
Exercise 2.1.3: Consider the functioning of a thermostat. The thermostat allows electricity to pass through the cables and puts a machine into action when the temperature drops below a limit, e.g., 70°F; whereas when the temperature rises above another limit, e.g., 90°F, then the thermostat cuts off the power and stops the machine. Construct a model of the functioning of the thermostat as a FA with a graph. Make the simplifying assumption that the temperature can only be of three kinds: a = “below 70°F”, b = “between 70°F and 90°F (including those two values)”, and c = “above 90°F”. Decide the states of the thermostat (let there be no final state), and when it passes from one state to another.
Definition: a
finite automaton is a 5-tuple
(Q, Σ, δ, q0,
F), where Q is a finite set of states, Σ
is a finite input alphabet, δ is a
transition function mapping Q X
Σ → Q, q0
![]() Q is the
initial state, and F is the set of
final states.
Q is the
initial state, and F is the set of
final states.
The transition function δ specifies which state q' the automaton moves to from each state q and each input symbol a; i.e., δ(q, a) = q'.
For example, the Elevator FA discussed earlier, has Q = {q0, q1, q2}, Σ = {0, 1, 2}, initial state q0, F = {q2}, and a δ given as follows:
| δ | 0 | 1 | 2 |
| q0 | q0 | q1 | q2 |
| q1 | q0 | q1 | q2 |
| q2 | q0 | q1 | q2 |
Definition: The deterministic finite automata, abbreviated as DFA, are automata such as these, in which each state and input symbol is mapped to a single state. (In the next subsection we’ll encounter the nondeterministic FA.)
Determinism regarding generally physical systems means that, given a current state and an input element, we know or can find out in which state the system will be next. Nondeterminism means we don’t know in which specific state the system will be, because it can be in an entire set of states.
The transition function δ can be easily extended to a function δ΄ so that δ΄ applies to strings, rather than single symbols, as follows:
-
δ΄(q, ε) = q
-
δ΄(q, wa) = δ (δ΄(q, w), a), for all strings w and input symbols a.
If we let δ΄ apply on a single input symbol a, we observe that δ΄(q, a) = δ(q, a) (the justification of this is left as an exercise). Thus, since there can be no confusion over which of δ΄ or δ is meant (their second argument, string or symbol, respectively, differentiates them), and since their effect on single symbols is identical, we shall drop the use of δ΄ and use δ instead, even on input strings.
Definition: a string x
is accepted by a finite
automaton M = (Q, Σ, δ,
q0,
F) if δ(q0,
x) = p, for some p
![]() F.
F.
If the string is not accepted by M, we say that it is
rejected by it.
Exercise 2.1.4: Consider the automaton depicted* in the following diagram:
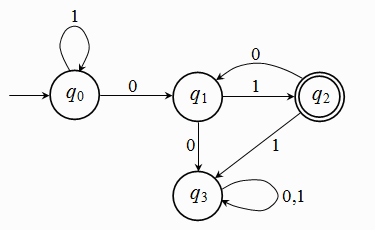
Fig. 2.1.3
Determine whether the above automaton accepts the strings: 01, 001, 111010101, 000010101, and 1110101010.
Exercise 2.1.5: The definition of a DFA (the only type of FA that we have seen so far) requires that the transition function δ is total, i.e., defined for every input symbol at every state. Consider the case of a partial δ, which is defined for all states, but not necessarily for each input symbol at every state. For example, the δ that appears in an earlier table (of the “elevator FA”) might be as follows:
| δ | 0 | 1 | 2 |
| q0 | q0 | q2 | |
| q1 | q0 | q1 | |
| q2 | q1 | q2 |
(This could correspond to an elevator with a few “dead” buttons.) Suppose we modify the definition of a DFA so that it can deal with partial transition functions, as follows: if the automaton finds itself in a state at which the input symbol is not defined (e.g., state q0 with 1 as the next input symbol in the above example) then the automaton rejects the input. Show that it is always possible to construct an equivalent* DFA with a total function δ that accepts and rejects precisely the same strings as those accepted and rejected by the DFA with the partial δ. ▓
Definition: the
language recognized by finite
automaton M = (Q, Σ, δ,
q0,
F) is the set of strings: {x | δ(q0,
x)
![]() F}.
F}.
Note that an automaton may accept many strings, but it will only recognize one language.
Note also that even if an automaton
does not accept even a single string, it still recognizes one language:
![]() , the
empty language.
, the
empty language.
We shall use L(M) to denote the language L recognized by finite automaton M.
Exercise 2.1.6: List a few more of the elements of the language recognized by the FA of Exercise 2.1.4. Now try to come up with an English description of all the strings in that language.
Definition: a language is called a regular set if it is the language recognized by some finite automaton. Such a language is also called a regular language.
Exercise 2.1.7:
Consider the language consisting of strings that are the binary
representations of integers n such that n
![]() 1
mod 4 (they yield a remainder of 1 when divided by 4). Is this a
regular language? If not, explain why. If yes, construct an FA that
recognizes it.
1
mod 4 (they yield a remainder of 1 when divided by 4). Is this a
regular language? If not, explain why. If yes, construct an FA that
recognizes it.
2.2 Nondeterministic Finite Automata
Earlier, we mentioned determinism in FA, which means that given a state q and an input symbol a there is only one arrow that leaves q and is labeled by a. (In other words, the transition function
δ is a true function.) We used the acronym “DFA” for the deterministic FA. Now we’ll meet the nondeterministic FA (“NFA”), in which, given a state q and an input symbol a, there can be more than one arrow leaving q and labeled by a. The NFA, in such a case, changes not to a single state, but to all states that are reachable from q through a. In other words, δ is not a transition function anymore, but a multi-valued mapping that maps q to a set of successor states.Another way to view the functioning of an NFA is that each time the automaton is presented with n choices for a given input symbol from a state, it “splits” into n copies of itself, and each copy keeps on working on the input independently of the other copies. Of course, this splitting can happen again: if one of the copies is presented with m choices, it splits into m copies again, each of which proceeds independently of any other copies that have been created at any time so far. Physicists must be familiar with this way of viewing the NFA’s, which is reminiscent of Hugh Everett’s “many-worlds interpretation” of quantum mechanics.
When can an NFA accept the input? It can if any one of its copies that work independently reaches a final state.*
The following is an example of an NFA:
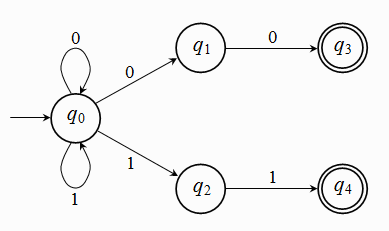
Fig. 2.2.1: example of an NFA
The above NFA accepts all strings of 0’s and 1’s that end either in 00 or in 11. It is nondeterministic because at state q0 there are two possibilities with input symbol 0: either staying at q0, or moving to q1. The same is true for input symbol 1, but a single such multiple choice suffices to characterize a FA as an NFA.
Exercise 2.2.1: Using the previous example as a guide, construct the graph of an NFA that accepts all English words ending in “-ed” and only them. (You may use shorthand notation to avoid drawing an edge for each letter of the alphabet.) Now think about how the graph would have to be constructed as a DFA. What do you observe?
Definition: a nondeterministic finite automaton (NFA) is a 5-tuple M = (Q, Σ, δ, q0, F), where Q, Σ, q0, and F have the same meaning as in the definition of a DFA, but δ is a mapping: Q X Σ → P (Q), where P (Q) is the power set of Q (the set of all subsets of Q).
Just as in the DFA’s, the transition mapping δ can be extended so that it accepts strings instead of single input symbols, in a similar way (the formal details are left as an exercise). Thus we can write: δ: Q X Σ* → P (Q). In addition, however, here it is useful to also extend δ so that it accepts sets of states, instead of single states: δ: P (Q) X Σ* → P (Q). This last extension is made as follows:
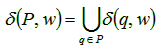
![]() P
P![]() Q.
Thus, we can talk again about L(M), the language recognized by
NFA M, as L(M) = {w | δ(q0,
w) contains a state q
Q.
Thus, we can talk again about L(M), the language recognized by
NFA M, as L(M) = {w | δ(q0,
w) contains a state q
![]() F}.
F}.
2.3 Equivalence of DFA’s and NFA’s
Intuitively, an NFA seems to be “more capable” than a DFA; that is, to be able to recognize more languages, because it can simulate a DFA (in the sense that every DFA is an NFA that doesn’t happen to have more than one resulting state per input symbol and state in its
δ). But, as we shall see immediately, this intuition turns out to be wrong: NFA’s recognize exactly the same languages as the DFA’s, i.e., the regular languages. This is stated in the following theorem:Theorem 2.3.1: a language L is recognized by an NFA if and only if it is recognized by a DFA.
|
Proof. The “if” part of the theorem is straightforward: if a language L is regular, i.e., recognized by a DFA, then that same DFA can be considered as an NFA, converting each state q of the DFA to a singleton set {q}, which is the corresponding state of the NFA. The “only if” part is a bit harder to prove, but it is based on the simple idea that, given an NFA that recognizes L, we can construct a DFA that recognizes the same L by “simulating” the functioning of the NFA at any point in time, mapping sets of states of the NFA into states of the DFA. That is, taking a snapshot of the NFA, considering all the states that each “parallel copy” of the NFA is currently in, and putting those states in a set {q1, ..., qi}, we’ll say that that set corresponds to a single state of the equivalent DFA. Let’s make this idea more precise. Let M = (Q, Σ, δ, q0, F) be an NFA recognizing L. We’ll construct the equivalent DFA M΄ = (Q΄, Σ, δ΄, q0΄, F΄) as follows. The states of M΄ are all the subsets
of the states of M. That is, Q΄ =
P
(Q). (Usually a subset, not all of those states will be used by the DFA; potentially, however, they can be all 2|Q|
states.) F΄ is the set of all states in Q΄ that contain a q
δ΄([q1,
q2,
...,
qi],
a) = [p1,
p2,
..., pj]
(The symbol “ It is easy to show by induction on the length of the input string x that: δ΄(q0΄,
x) = [q1,
q2,
...,
qi]
Inductive basis: for |
x | = 0 (i.e., x = ε)
we have trivially that δ΄(q0΄,
ε)
= [q0]
Inductive step: suppose
that the hypothesis is true for inputs of length n or
less. Let xa be a string of length n + 1, with a
δ΄(q0΄, xa) = δ΄(δ΄(q0΄, x), a). By the inductive hypothesis,
δ΄(q0΄,
x) = [p1,
p2,
..., pj]
But, by the definition of δ΄, δ΄([p1,
p2,
..., pj],
a) = [r1,
r2,
..., rk]
Thus, δ΄(q0΄,
xa) = [r1,
r2,
..., rk]
establishing the inductive step. To complete the proof, we must
add that δ΄(q0΄,
x)
|
Exercise 2.3.1: Consider the NFA depicted by the following graph:

Fig. 2.3.1
This NFA accepts all strings with a prefix of zero or more 0’s and a suffix of 0 or 1. Using the proof of the above theorem 2.3.1, construct a DFA that’s equivalent to this NFA. Before starting, answer the question: what is the set F΄ of the equivalent DFA? ▓
What is the usefulness of NFA’s? Besides being useful as an introduction to the notion of nondeterminism, they also have an inherent usefulness: they simplify the structure of the automaton, in many cases, as shown in the following exercise.
Exercise 2.3.2: Try to express the DFA of exercise 2.3.1 with a minimal number of states. Hint: you will find out that it cannot be realized with a number of states smaller than three. ▓
The NFA’s are also useful in helping us realize that adding an apparent “extra ability” to an automaton (such as the ability to move to multiple states on a single input symbol) does not add anything to the computational power of the automaton. When we examine the most powerful type of automata, the Turing Machines, we’ll see that this is also true in that case. Now we’ll add one more feature to our NFA’s, only to realize the same idea.
2.4 NFA’s with
ε-Moves
T O B E C O N T I N U E D . . .
3. Context Free Grammars
T O B E C O N T I N U E D . . .
Footnotes: (Clicking on
^ returns to the point in the text where a reference to the present footnote is made)^ We say that points, lines, etc., belong to the “ontology” of geometry; that is, in the set of notions with which geometry is concerned. Similarly, symbols (just as strings, alphabets, languages, etc., which are defined immediately below in the main text) belong to the ontology of the present theory.
^ Note that terms such as “cardinality” belong to set theory, therefore in the prerequisites of this course. The same is true for every other term the definition of which is not given in this text, such as: “function”, “relation”, “union”, “intersection”, etc.
^ We do not need to repeat the “and only if” in definitions from now on. We remind the reader that in mathematics every definition is understood always as an “if and only if” statement.
^ This name is pronounced /'klee·ni/ or /kleen/ by practically all native speakers of English. However, Stephen Cole Kleene himself was pronouncing it as /'klei·ni/ (same source).
^ The reason that trees are shown “reversed” (upside-down) is obvious: reading is done from top to bottom, and the natural starting point for reading the diagram of a tree is its root.
^ From now on we shall speak of an FA “depicted” in a diagram showing a graph, by which we shall assume that the input alphabet consists of only the symbols shown in the graph, and the transition function δ is exactly the one shown by the edges of the graph.
^ The notion of equivalence of FA’s will be examined in later sections. Right now, intuitively, we can say that two FA’s are equivalent if they accept the same set of strings (or “recognize the same language” — a term defined immediately below in the main text).
^ When an NFA is implemented in a computer, and the task is to decide the acceptance or rejection of a given input, then — contrary to the mentioned “many-worlds interpretation” — a mechanism must be present in the program so that if any of the parallel processes, each of which implements a copy of the NFA, terminates, it informs the rest of the processes to cease running; this is so because in computers it is desirable that programs stop running as soon as possible. But if the task is to list a number of the accepted strings of the (possibly infinite) recognized language, then this “parallel processes terminate” signal is unnecessary.
Bibliography
-
Hopcroft, John E., and Jeffrey D. Ullman (1979). Introduction to Automata Theory, Languages, and Computation. Addison Wesley, Reading, Massachusetts.
-
Papadimitriou, Christos E. (1994). Computational Complexity. Addison Wesley, Reading, Massachusetts.
-
Sipser, Michael (2013). Introduction to the Theory of Computation (3rd ed.). Cengage Learning, Boston, Massachusetts.