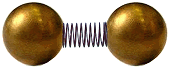Mach’s bucket, and a non-puzzle for a non-physicist
Will some physicist please explain what appears as a
non-puzzle to me?
This page is part of the author’s
topics in physics.
Dear reader, consider this page the equivalent
of a message in a bottle, thrown into the cyber-ocean with the
hope that it is picked up by some real physicist, who will kindly
explain to me where the puzzle is. However, the text is written
with a general audience in mind. The puzzle I am talking about is
a question that was initially put forth by Newton, who answered
it to his own satisfaction; it was then re-examined by Ernst Mach
in the 19th C., who disagreed with Newton and gave his own
answer. Today — as far as I know — it is assumed that
Einstein’s framework gives a satisfactory answer to it. I don’t
disagree with any of the previously mentioned gentlemen. I simply
don’t understand why there is a question at all. Why have
several of the brightest minds, including some contemporary ones,
been concerned with something that appears to have a really
trivial answer? (You’ll see what I mean after reading.) Will
somebody please explain to the author, a scientist but
non-physicist? But first, it is I who has to explain what the
puzzle is.
It’s the puzzle of the bucket
 |
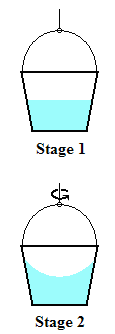
Take a bucket of water,
said Newton. Buckets usually come with a semi-circular
handle (see figure, on the left). Bind a rope from the
middle of its handle, and hang the rope from somewhere,
with the bucket filled with water up to the middle. Now
start rotating the bucket around the vertical axis that
coincides with the rope, so that the rope becomes
twisted, as in the figure. Then let go. What will happen
to the surface of the water? Stage
1: In the first moments after you let the system
loose the surface of the water will be flat (top figure
on the right). As the bucket picks up speed while
spinning, its rotating wall will cause the water,
reluctantly, to follow it into the rotating motion by
friction. Stage 2: When the water
rotates somewhat fast, its surface will become concave
(bottom figure on the right).
Now stop the bucket abruptly! Stage
3: The water will continue rotating for awhile,
its surface retaining the concave (parabolic,(*)
actually) shape, until finally it
comes slowly to a rest, with its surface back to the flat
state. That’s Newton’s bucket experiment.
Newton thought like this: that the
surface of the water becomes concave proves that the
water is rotating. But with respect to what is it
rotating?
|
 |
It can’t be rotating with respect to the
bucket, because at stage 2 both the water and the bucket were
spinning at around the same speed, thus they were stationary
with respect to each other, yet the water had a concave
surface. When we stopped the bucket at stage 3, the water was
rotating with respect to the bucket, but then it slowed down and
its surface became gradually flat. So we see that the shape of
the surface cannot be predicted by the relative motion between
bucket and water: just by looking at what the bucket does
(spinning or not) you can’t tell what the surface of the water
will look like. So if the water is rotating, said Newton, it
must be rotating with respect to absolute space. Thus Newton
thought he brought up evidence for the existence of absolute
space. That was late 17th century.
Enter Mach. This is the second half of the 19th
century, and Ernst Mach does not believe in Newton’s absolute
space, but is a relativist (soon to influence Einstein and his
relativity, according to some), following in the steps of another
great relativist, Gottfried Wilhelm von Leibnitz, who was Newton’s
contemporary. Mach thought, what if the bucket were placed away
of all things with mass in the universe? What if the bucket were
the only thing in the universe? Would it still rotate?
But with respect to what? How can one say that something is
rotating if there are no landmarks around to verify its rotation?
Would the water in the bucket still acquire a concave surface in
a bucket-only universe? Okay, water needs gravity in order to
stay in the bucket, and since we don’t have gravity in such a
universe (call it a “Mach universe” from now on), Mach
replaced the bucket-plus-water with two bricks tied together with
a rope, and asked whether rotation would tighten the rope or it
would stay loose (implying that no rotation is possible in such a
universe). But I don’t have a conceptual problem with the
bucket-and-water setup. Put iron filings in the bucket instead of
water, and a powerful magnet underneath, to simulate gravity. All
right, the magnetized iron filings will not form a smooth surface
like water does, but either they will be deformed by rotation or
not — you get the idea. Besides, adding a magnet is no big deal
because, in any setting, we must also assume an observer who can
see the result of the experiment and form an opinion. What Mach
wanted to exclude was the mass of stars in the rest of the
universe, he didn’t care about the insignificant masses of an
observer, or a magnet, or the bucket itself. And if you insist
that water or some liquid is essential, put a whole Earth-sized
planet underneath the bucket! Mach would still not mind; a planet
more or less is so insignificant compared to the totality of the
universe that it wouldn’t make any difference in Mach’s
argument. So I’ll keep talking about the “water in the bucket”
experiment, keeping in mind that it might require some technical
modifications for it to work, depending on the environment. (This
will also save me from having to make another drawing showing
bricks and ropes, by the way.)
Mach said: Nobody can know by observation
whether the surface of the water would become concave in that
setting, so we can only speculate about the event. And Mach did
speculate: he said, in such a special universe, the water would not
become concave, because it would not rotate, having nothing
to rotate with respect to. What causes the force that we
feel and describe as “centrifugal” is the mass of the fixed
stars, i.e., the rest of the universe, he said. The water rotates
relative to that, in our universe. But, subtract the stars and
everything else (except the apparatus necessary for the
experiment) and there will be no rotation, because Newton’s “absolute
space” is nonexistent.
By Mach’s reasoning, if we inserted a single
star in a Mach universe, there would be the faintest centrifugal
force while the water would be rotating with respect to that
single star, and the faintest dent on its surface. As we kept
adding stars, approaching the mass of our familiar universe, we
would likewise approach the observation of the familiar
bucket-plus-water experiment.
The reader can find a
nice reference to read all the above in Brian Greene’s “The
Fabric of the Cosmos”.[1] In the same
book, Greene tells us what the present-day verdict about Newton’s
and Mach’s bucket is: according to general relativity, granted,
there is no Newton’s absolute space, but there is Einstein’s absolute
spacetime, and that is with respect to what the water
rotates, and thus acquires its concave surface.
(So, my understanding after all this is that
Einstein would agree with Mach: in a specially crafted universe
that contains only the experimental apparatus and nothing else,
the water surface would remain flat because the absolute
spacetime would be absent. At least this is implied by Greene’s
book. This does not affect in any way what I am about to
describe, but correct me please if my understanding of Einstein’s
view is wrong.)
What is the significance of a water bucket anyway?
The water-in-the-bucket experiment is really
about inertia and mass. In Newton’s view, because we and
everything else are immersed in absolute space, we feel a force
when we accelerate (or decelerate) with respect to that space.
Note that every object that does not move at constant speed along
a straight line experiences acceleration (in the general sense,
including deceleration), and so do the water parts, since they
move circularly. In Mach’s (and I suppose Einstein’s, and
Greene’s, etc.) view, we feel that force because we accelerate
with respect to the distant fixed stars (with respect to absolute
spacetime, as per Einstein, etc.). Without a frame of reference,
in a relativistic universe there can be no acceleration, no force
felt, no inertia.
I don’t know if physicists would say the
water and the bucket still have mass, even in a Mach universe.
Perhaps they do have mass, but without inertia we would be unable
to measure their mass in the familiar way, i.e., by how much
force they exert on something that accelerates them, because they
can’t accelerate. I conclude that if you kicked the bucket
(literally, not figuratively!) in such a universe, you’d feel
nothing, no force against your foot, otherwise you’d be able to
measure its mass (perhaps in a painful way).
Is all this fuss with the absolute-whatevers necessary?
I think not. I think neither distant fixed
stars, nor absolute spacetime is necessary for inertia to be
observed, and this is what I hope some physicist will kindly
either confirm, or reject (and explain the rejection), after
reading my explanation. I think the water in the bucket can
rotate even in a Mach universe, and will acquire a
concave surface. Allow me please to explain my thought: why no
reference frame based on distant stars or absolute spacetime is
needed for acceleration and inertia.
The claim that I explain below is that the
water would rotate with respect to the frame defined by
itself and the bucket. But before we can see that, it’s
better to consider a situation as simple as possible.
Suppose I am in a Mach universe, standing
nowhere, and have in front of me two ball bearings connected with
a metal spring. I approach my finger to the ball on the right (as
in the figure below), and try to push it. What will happen?
Will the spring be compressed, causing the ball
on the right to approach somewhat the ball on the left, as the in
following figure?
I think it will. I can find no physical reason
to explain how the absence of mass in the rest of the universe
will prevent the spring from being compressed. To see this, we
can examine what would happen at the biological and molecular
level.
First of all, would I be able to move my arm?
I guess so, because the energy required for my
muscles to contract and extend is produced by the mitochondria of
my cells, the function of which is based on some chemical
reactions. Those reactions have nothing to do with stars, nearby
or faraway, fixed or moving. My muscles will work, and my finger
will approach the rightmost ball. Will the ball be pushed?
Again, I think yes, it will. When my finger is
about to touch the ball, at the molecular level, the outermost
atoms of the molecules of my finger will approach the outermost
atoms of the molecules of the ball. Atoms will approach atoms.
This means the electrons of the outermost shells of those atoms
will approach the electrons of the outermost shells of the other
atoms. Electrons will approach electrons. When the electron
shells will come too close, virtual photons will be exchanged
probabilistically (at times not determined by any of the laws of
physics we are aware of today), and the two atoms will recoil.
This is the basic functioning of the electromagnetic force. It is
the same force that allows you to sit somewhere now and not pass
through objects like a ghost. The electromagnetic force will
work, as it always does, independent of distant stars, planets,
their alignment, and your horoscope. Why should two electrons
care whether the rest of the universe exists?
Now, the recoiling atoms will propagate their
action to nearby atoms, and those to nearby atoms, and so on,
throughout the mass of the impacting bodies (the ball and
myself). This is described theoretically through phonons,
which are entities that I don’t pretend to have understood, but
I don’t think I am missing something essential here. The point
is, the impact will be propagated through the two bodies that
collided. Assume that my mass is substantially larger than the
mass of the ball (contrary to what that wimpy hand in the figure
above suggests). When I say “my mass is larger” I mean I have
many more particles (e.g., molecules) than the ball. Given this,
my molecules will take longer to react as a whole to the impact
than the fewer molecules of the ball, and this is why a more
massive body moves back (recoils) slower after its impact with a
less massive body, which recoils faster. So the molecules of the
ball (i.e., the ball itself) will tend to move as a whole to the
opposite direction from the one I will move, only faster than me.
Now, there is a spring there. Will the spring
be compressed?
Of course it will, and for the same reason for
which the ball moved. I don’t need to repeat the explanation in
detail, it’s again the electromagnetic force that causes the
molecules of the body of the spring to acquire such positions in
space that give to the spring its compressed shape. Stars have
nothing to do with this.
But the job of a spring is to extend as soon as
it is compressed, so the spring will push the leftmost ball
further to the left. If I stop exerting any force, the system
will come to the original equilibrium (spring extended) after a
short vibration, the duration of which depends on how sturdy the
spring is: if the spring is very pliable, the vibration will last
a bit longer.
But suppose I continue exerting the force on
the right. I continue acting with a constant force F. What will
happen then?
My guess is that the spring will remain
compressed (again, after a brief vibration, but coming to a new
equilibrium in a more compressed state), as in the figure below.

I know, there is no
wall on the left pushing against the leftmost ball and preventing
it from moving, and in a Mach universe there is really nothing
for the ball to move “into”.(*) But my force F
is applied constantly. The spring would extend back to its
original shape if I stopped applying the force. As long as the
force acts, the spring will remain compressed. This happens also
in our familiar universe, and has nothing to do with stars. The
difference is that in our universe we’ll see the whole system accelerating
with respect to its surroundings, because there are surroundings
and we can register and measure its acceleration. In a Mach
universe there are no surroundings to use as landmark objects, so
we won’t be able to observe any acceleration, but this doesn’t
mean that the spring will not be compressed! The compression of
the spring is a molecular phenomenon, independent of external,
landmark objects.
This is the important conclusion from all the
above: that the apparatus of the two balls will be compressed with
respect to itself; that is, with respect to a frame of
reference defined by the apparatus itself, and such a frame of
reference can always be defined, since we assume that the
apparatus occupies some space, however little space a
Mach universe can provide.
Exactly the same reasoning can be applied to
the water bucket system: a frame of reference can be defined by
the system itself, and the water can be observed rotating with
respect to that frame of reference. Indeed, the thought
experiment with the balls connected by a spring that was
described above is directly applicable to the water bucket
experiment, because we can abstract the water molecules by little
balls (for the purposes of this discussion), and the role of a
spring is played by the intermolecular forces that keep water
molecules at a certain distance from each other. It’s again the
electromagnetic force that prevents water molecules from coming
too close to each other. (There aren’t many forces in nature,
there’s only four of them: strong, weak, electromagnetic, and
gravity, and of the four, only the electromagnetic force is
relevant in keeping molecules from colliding.) When a molecule is
“pushed” through the electromagnetic force (the “spring”),
it likewise “pushes” its neighboring molecules, and so on.
It remains to be convinced that the water will
acquire a concave surface in the Mach universe.
 |
First comes the question: will the
bucket, with the rope twisted and then let free, rotate
with respect to the rope? (Remember, there is a force
pulling it “down”: if we use iron filings, it’s the
magnetic pull of the magnet, and if we use water, then
it’s the gravitational pull of the planet; I use
“water” in this text to mean either of the two
setups.) Yes, the bucket will
rotate, because the forces that cause the twisted string
to unwind are entirely local (considering the pulling
force as a local one, too) and do not depend on the
faraway stars. They are forces developed due to the molecular
arrangement of the strings that form the twisted
rope. (Need I mention it again? It’s the
electromagnetic force.) “With respect to the rope”
means that while the rope is unwinding slowly, the bucket
rotates faster with respect to it.
|
Next, consider a body on a rotating plane
(figure, below). Will the body tend to be pushed to the sides of
the rotating plane?
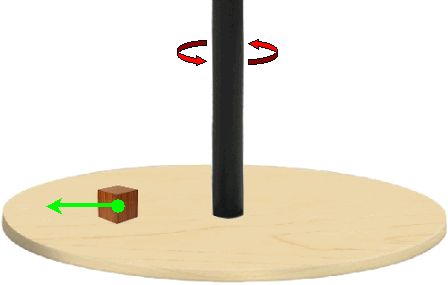
The cube shown on the round table, above, is
pushed to the circumference of the table because of a so-called
“fictitious centrifugal force”. That is, if our frame of
reference is the table, then it appears as if a force is acting
on the cube (green arrow) that pushes it toward the
circumference. Alternatively, if we fix our frame of reference to
a non-rotating one with respect to the table, then there is no
force acting on the cube. The latter simply tends to retain its
state of non-rotation, and when the table rotates it forces the
cube to go in a circle; the combined result of the cube tending
to retain its non-rotation and of it being forced to move along a
tangent to its circular path is that it follows a route that
brings it closer to the circumference (unless friction holds it
in place).
This is all elementary, high school physics,
and it rests on our ability to consider a fixed frame of
reference with respect to which the table rotates, if we want to
avoid fictitious centrifugal forces. But we do have such a frame
of reference in our water-bucket experiment. Recall that we have
a non-rotating or slowly-unwinding rope, and that the bucket
rotates faster relative to the rope.
Now, one might think, Mach might want to get
rid of the rope, if he were alive to counter this argument. He
might request the existence of a bucket with water only, or of
two bricks tied by a rope, as indeed was one of his formulations
of the problem.
But this is not possible. Something
must set the system in rotating motion (or attempt to
set it in rotating motion, if Mach insisted it wouldn’t
rotate). There must be some mechanism: a twisted rope, an
observer’s finger stirring the water (or pushing the bricks), something
anyway. Magic alone will do nothing to a mere bucket with water.
| The moment we introduce a mechanism to
effect the circular motion, we can fix a frame of
reference to that mechanism, relative to which the bucket
will rotate. |
It is not possible to have a pure body (e.g., a
bucket with water only) without any apparatus to rotate it, and
ask whether the pure body can rotate in an empty universe. Mach
can’t have the pie whole and eat it.
Essentially the argument above says that the
entire system prior to the rotation defines a fixed
frame of reference. After the rotation, the part of the apparatus
that causes the rotation and doesn’t rotate (there must be
some) remains immobile in that frame of reference. The rest of
the system rotates with respect to the fixed frame. Neither
distant stars, nor absolute spacetime is needed.
As for the final conclusion about the shape of
the water surface, it’s easy. Think of water molecules as
bodies like the cube on the table, in the figure above. Consider
one such molecule, closest to the bucket wall, and on the top
surface of the water (golden ball in figure, below).

The green arrow in the figure above shows the
direction of motion of the molecule due to the rotation of the
bucket (as in the cube-on-table case, in an earlier figure).
However, motion along that direction is impossible, because the
molecule is prohibited by the molecules of the bucket wall (shown
in solid brown, on the left). The only way of moving is along the
direction of the red arrow. As soon as this molecule moves along
the red arrow, its location is emptied and can be occupied by
other molecules, and so on. This causes some of the molecules
close to the wall to move up, leaving an empty space that becomes
progressively larger as we move toward the center, which gives
the overall concave shape to the surface of the water. The situation involving real
molecules is much more complex than the ideal metallic balls
shown in the figure above, but, roughly, the principle is the
same.(*)
The above concludes the argument by which I
understand that the water will acquire a concave surface after
rotating in a Mach universe, without needing to resort to notions
such as distant stars or absolute spacetime to explain why. If
there is any error in my reasoning, or if you have other
suggestions, corrections, or comments, please feel free to contact me and let me know.
Post Scriptum, Summer 2012
After some experimental confirmation regarding the existence
of Higgs boson and the ensuing discussion, it is now my understanding that, for
inertia to exist, the system must be immersed in a Higgs field. Roughly
speaking, the more massive an object is, the harder it is for it to change its
state of motion as it makes its way through the Higgs field. An elephant has
more particles than a bee. It’s harder for the elephant to change his state of
motion than the bee, because many more particles from the elephant’s body than
those of the bee need to negotiate with the ubiquitous Higgs field. At least
that’s my naïve understanding. Now, how does this
change any of the things stated earlier on this page? I’m still trying to figure
that out.
What I do understand is that Einstein’s absolute space-time is
not the reason for the existence of inertia. The true reason is the
existence of Higgs field, which permeates our familiar universe and its
space-time.
Footnotes: (Clicking on the footnote caret
(^) brings back to the text)
-
(^) Thanks to Phil Jilbert, from the UK, for pointing this out.
- (^) Of course the
apparatus of the two balls and the spring will be pushed away
from me. How far it will go, or how far I can keep on
pushing it, depends on the size and properties of the
Mach universe. But for this thought experiment to work
there is no requirement that the apparatus must move far
from the observer, or stay close — no fixed frame of
reference is required here; we only need to observe
whether the spring will be compressed or not.
- (^) Note that the slope of the bucket wall is
inconsequential: even with a vertical wall (or even with
one reclining in the opposite direction) real molecules
will find the way to “glide” on top of each other,
unlike balls in the macro-world that can be hindered by
friction.
References:
[1]
Greene, Brian R. (2004). The fabric of the cosmos: space,
time, and the texture of reality. New York: Knopf.
Back to Harry’s index to topics in
physics
Back to Harry’s home page