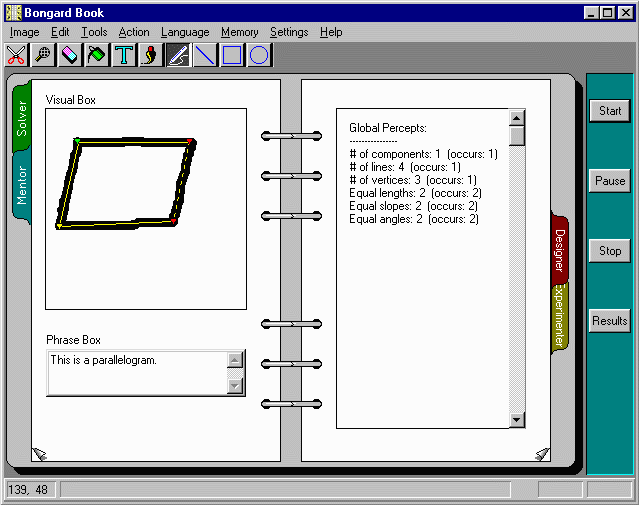

The picture above shows graphically some of the results of visual analysis done on the given input (the parallelogram), after pressing on the "Start" button. Notice that the picture is captured from an earlier version of the program. It has not been updated since because the visual analysis is now more complex (more features are perceived and shown graphically), and would be harder to explain. Also notice that the analysis was interrupted (by clicking on the Pause button) at an early stage, roughly 1/2 second after it started.
Yellow lines show the approximation of "median lines" done by the program on the thick, hand-drawn actual lines. At this early stage, three of the yellow median lines are continuous, while the fourth one is dotted: this is a rough way to show the "certainty" with which Phaeaco created those lines. Further analyis would add more points to the fourth line, and would make it appear continuous, too.
Intersection points, or rather, vertex points in this case, are shown with a small inverted colored triangle. In other cases, a small square depicts touch points (as the one formed by the two lines of letter T), and a small diamond depicts cross points (as in letter X). More complex intersections (as in letters K and Y) are depicted with a small star. The color of the intersection point shows the certainty with which the program sees this as such a point. This certainty is directly related to the certainty of the lines forming the intersection. For example, the two vertices on the right side of the parallelogram are shown with red color (lowest certainty) because the program is still uncertain about the constituent right side (dotted line). The other two vertices on the left have yellow and green colors because the program is more certain about their constituent lines. The colors used for intersection points are red, orange, yellow, green, cyan, and blue, in increasing order of certainty.
Other visual compenents that can be depicted graphically on the input are: border lines, when the "black" portion of the input is not sufficiently linear, and thus defines a filled (black) area, cuves, areas (either filled, or outlined ones), and more.
It should be noted that all the above color-coded components provide just a superficial glimpse over the progress of visual analysis. A better report can be obtained at the end of processing, part of which is shown on the right page of the notebook, above. The information on the right shows that Phaeaco found the following features and relations:
It should be noted that Phaeaco is not as good at counting as the above description might suggest. When the numbers are small (up to about four or five), counting is generally accurate. However, as the actual number of occurrences (of various percepts) increases, Phaeaco's reporting of quantities (the "numerosity" in psychological jargon) becomes increasingly blurry and inaccurate. For example, if ten straight lines exist in the input, the lowest level line-detecting processes will actually identify all of them, but when the time comes to estimate and report their number Phaeaco will register a statistical quantity with mean value of around ten, and a certain standard deviation. The larger the actual number, the larger the standard deviation. If Phaeaco is asked to report a specific number, it may report any number around the mean, allowed by the deviation. What happens in the report shown on the picture above is that the deviation for numbers up to five is almost zero, so the exact number is reported.
Last update: 04/14/00
Back to Mentor Section