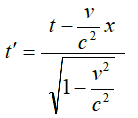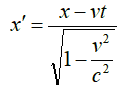 |
Ειδική Σχετικότητα και Στοιχεία Γενικής ΣχετικότηταςΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ Φ2 ΤΟΥ Δ.Ε.Π.
|
Στόχος και εύρος του μαθήματος· προαπαιτούμενα
Το παρόν μάθημα αποτελεί μια εισαγωγή στη θεωρία της σχετικότητας, που γίνεται με τρόπο ώστε οι στοιχειώδεις έννοιες της θεωρίας να γίνουν κατανοητές ακόμα και από όποιον έχει απλή γνώση φυσικής του γυμνασίου–λυκείου. Η παρουσίαση ακολουθεί το παράδειγμα των εκλαϊκευτικών βιβλίων του Αϊνστάιν,(*) χωρίς όμως να αποτελεί αντιγραφή κανενός από εκείνα. Το πνεύμα των βιβλίων του Αϊνστάιν είναι οτι, προκειμένου ο συγγραφέας να απευθυνθεί σε όσο το δυνατόν πιο ευρύ ακροατήριο, πρέπει να είναι φειδωλός στη χρήση μαθηματικών εξισώσεων. Εξισώσεις χρησιμοποιούνται μόνο εκεί όπου είναι απαραίτητες για την καλύτερη κατανόηση του αντικειμένου, και μόνο τέτοιες ώστε να μην απαιτείται γνώση ανώτερων μαθηματικών· είναι δηλαδή απλής μορφής, και — τουλάχιστον στην ειδική σχετικότητα — περιλαμβάνουν μόνο γυμνασιακού επιπέδου πράξεις, όπως η τετραγωνική ρίζα και η ύψωση σε δύναμη.
Με την ολοκλήρωση των παραδόσεων του μαθήματος, ο διδασκόμενος αναμένεται να αποκτήσει μια “αίσθηση” της αντίληψης του χώρου και του χρόνου που είναι πολύ διαφορετική από την οικεία-μας μέσω της καθημερινής εμπειρίας.
Αντίθετα από την πρακτική του Αϊνστάιν, που ξεκινούσε με ανασκόπηση των εννοιών του χώρου και του χρόνου στην κλασική φυσική, εμείς εδώ θα ξεκινήσουμε “κατευθείαν” από τη σχετικότητα, ανακαλύπτοντας τη διαφορετικότητα του σχετικιστικού κόσμου (έτσι δηλαδή όπως είναι στην πραγματικότητα) από τον “παραμορφωμένο” κόσμο τον οποίο αντιλαμβανόμαστε με τις αισθήσεις-μας.
1. Ειδική Σχετικότητα
1.1 Προσπάθειες μέτρησης της ταχύτητας του φωτός
Από το 17ο αιώνα ήδη είχε τεθεί το ερώτημα: ποια να είναι η ταχύτητα του φωτός; Μπορεί άραγε το φως να μεταδίδεται ακαριαία από το ένα σημείο του χώρου στο άλλο; “Ακαριαία” θα πει οτι τη στιγμή που πατώ το διακόπτη, το φως της λάμπας το βλέπει όποιος μπορεί να δει τη λάμπα την ίδια στιγμή, οσοδήποτε μακριά κι αν είναι ο παρατηρητής. (Και επειδή τον 17ο αιώνα δεν υπήρχαν διακόπτες και λάμπες, μπορούμε να φανταστούμε κάποιον να αποκαλύπτει το φώς ενός κεριού ή δάδας, αποσύροντας ένα αδιάφανο κάλυμα.) “Ακαριαία” λοιπόν θα πει άπειρη ταχύτητα, όχι απλώς πολύ μεγάλη· θα πει, το φως να το βλέπει ο παρατηρητής όχι απλώς “σε χρόνο dt” (όπως λέμε μερικές φορές στην καθομιλουμένη, δανειζόμενοι αυτόν τον όρο της φυσικής), αλλά σε χρόνο μηδέν. Άλλη δυνατότητα ήταν να έχει το φως πολύ μεγάλη ταχύτητα, και μάλιστα τόσο μεγάλη που κάθε απόπειρα εκείνης της εποχής να μετρηθεί είχε αποτύχει: το φως εμφανιζόταν να “τρέχει” πολύ πιο γρήγορα απ’ όσο μπορούσαν να μετρήσουν τα όργανα εκείνου του καιρού. Πράγματι, το 1676 ο Δανός αστρονόμος Ole Rømer, μελετώντας την περιφορά του δορυφόρου Ιώ γύρω από τον πλανήτη Δία, έδειξε οτι η ταχύτητα του φωτός δεν είναι άπειρη αλλά συγκεκριμένη — παρόλο που δεν μπόρεσε να υπολογίσει πόση ακριβώς ήταν.
Έπειτα, υπήρχε και το συναφές ερώτημα: μέσα σε ποιο μέσο μεταδίδεται το φως; Ο ήχος, για παράδειγμα, μεταδίδεται μέσα στον αέρα, στο νερό, στα στερεά, κλπ.· και μάλιστα όσο πιο “πυκνό” το υλικό, τόσο μεγαλύτερη είναι η ταχύτητά του. Χωρίς κάποιο μέσο όμως, δηλαδή στο κενό, ο ήχος δεν μεταδίδεται. Αυτό ήταν γνωστό ήδη από τον 18ο αιώνα, όταν οι επιστήμονες μπορούσαν να φτιάξουν αρκετά καλά κενά μέσα σε σωλήνες, αφαιρώντας τον αέρα, οπότε είχαν παρατηρήσει τη μη μετάδοση του ήχου μέσα στο κενό. Το φως όμως; Πώς φτάνει σ’ εμάς από τον Ήλιο, το Φεγγάρι, και τα άστρα; Οι μελετητές της φύσης ήσαν αρκετά σίγουροι, από τότε, οτι μεταξύ Ήλιου και Γης δεν υπάρχει αέρας αλλά κενό. Είχαν δηλαδή τη σωστή αντίληψη, παρ’ όλο που δεν υπήρχαν τότε διαστημικά ταξίδια. Ίσως ένας λόγος γι’ αυτό να ήταν η αρχαία θεωρία του Αριστοτέλη, που έλεγε οτι τα ουράνια σώματα κινούνται εντός του “5ου στοιχείου” της φύσης, που ο Αριστοτέλης ονόμασε “αιθέρα”. Πρέπει να γνωρίζουμε οτι την εποχή του Αριστοτέλη (4ος αι. π.Χ.) επικρατούσε η θεωρία του Εμπεδοκλή, περί “τεσσάρων στοιχείων” από τα οποία υποτίθεται αποτελούνται όλα τα υλικά: γη, νερό, αέρας, και πυρ. Ο Αριστοτέλης λοιπόν είχε προσθέσει ένα πέμπτο, τον αιθέρα, γιατί — συλλογίστηκε — δεν είναι δυνατόν τα “τέλεια” ουράνια σώματα — Ήλιος, Σελήνη, πλανήτες, κλπ. — να κινούνται εντός “ατελών” μέσων όπως ο αέρας ή το νερό. Άρα χρειάζεται ένα “τέλειο” μέσο, και αυτό το ονόμασε “αιθέρα”. Τον 18ο και 19ο αιώνα λοιπόν, οι επιστήμονες θεώρησαν οτι αυτό το μέσο, ο αιθέρας, είναι που “γεμίζει” αυτό που ονομάζουμε κενό, και έτσι καταφέρνει και μεταδίδεται το φως, π.χ. από τον Ήλιο στη Γη: κινούμενο μέσα στον αιθέρα.
Εδώ να προτρέξουμε λίγο, ανοίγοντας μια παρένθεση. Τον 20ό αιώνα, και χάρη στη θεωρία της σχετικότητας, οι επιστήμονες πίστεψαν οτι κατάφεραν επιτέλους να αποδείξουν οτι ο αιθέρας δεν υπάρχει. Και πράγματι, τώρα στις αρχές του 21ου αιώνα, τα εγχειρίδια φυσικής απηχούν ακόμα αυτή την άποψη: πως ο αιθέρας είναι ανύπαρκτος. Θα δούμε όμως λίγο αργότερα, οτι κατά τον 21ο αιώνα τελικά αποδείχτηκε οτι υπάρχει κάτι που “διαπερνά” τα πάντα, και που θέτει υποψηφιότητα για την υλοποίηση της αρχαίας ιδέας του Αριστοτέλη περί αιθέρα: ονομάζεται “πεδίο Χιγκς” (Higgs field), και είναι υπεύθυνο για τη μάζα κάθε υλικού σώματος, για το γεγονός οτι όταν επιταχυνόμαστε αισθανόμαστε μια δύναμη να μας τραβά προς τα πίσω· όπως και όταν φρενάρουμε, οπότε αισθανόμαστε μια δύναμη να μας ωθεί προς τα μπρος. Πάντως το πεδίο Χιγκς αλληλεπιδρά μόνο με σώματα που έχουν μάζα. Το φως όμως δεν έχει μάζα, και γιαυτό περνά μέσα από το πεδίο Χιγκς εντελώς ανεμπόδιστα. Έτσι, το πεδίο Χιγκς έχει κάποιες από τις ιδιότητες του αιθέρα (π.χ. αποτελεί ένα σταθερό “σύστημα αναφοράς”), αλλά όχι όλες: π.χ. δεν μεταφέρει το φως (αφού το φως δεν αλληλεπιδρά με αυτό), άρα δεν μπορούμε να πούμε οτι παίζει το ρόλο του “φωτοφόρου αιθέρα” (έτσι ονόμαζαν τον αιθέρα μέχρι τον 19ο αιώνα). Θα καταλάβουμε προς το τέλος της ενότητας περί ειδικής σχετικότητας ποια είναι η σημασία της ύπαρξης του πεδίου Χιγκς για το θέμα-μας, και πώς ανατρέπει κάποιες απόψεις περί ειδικής σχετικότητας που είχαν παγιωθεί στη σκέψη των φυσικών του 20ού αιώνα — χωρίς όμως να ανατρέπει την ίδια τη σχετικότητα. Κλείνουμε εδώ την παρένθεση, και επιστρέφουμε στα ερωτήματα της ταχύτητας του φωτός, και του μέσου στο οποίο κινείται.
1.1.1 Το πείραμα των Michelson – Morley
Περί τα τέλη του 19ου αιώνα, δύο Αμερικανοί φυσικοί, οι Michelson (Μάικελσον) και Morley (Μόρλι),(*) σκαρφίστηκαν ένα πανέξυπνο πείραμα για να αποδείξουν την κίνηση του φωτός μέσα στον αιθέρα· να αποδείξουν δηλαδή την ύπαρξη του αιθέρα, και να φανεί οτι το φως κινείται μέσα σ’ αυτόν. Τον πειραματισμό αρχικά ξεκίνησε μόνος-του το 1881 ο Michelson, ο οποίος σκέφτηκε οτι αν η Γη (μαζί με όλους εμάς) κινείται μέσα στον αιθέρα (βλ. σχεδιάγραμμα παρακάτω), θα πρέπει να δέχεται έναν “αιθέριο άνεμο”· όπως ένας κολυμβητής που βρίσκεται μέσα σε θαλάσσιο ρεύμα, οπότε αν θέλει να κολυμπήσει προς μία διεύθυνση (ή και απλώς να μείνει ακίνητος) νοιώθει να σπρώχνεται προς μία διεύθυνση. Ο “κολυμβητής” είναι το φως, σκέφτηκε ο Michelson. Αν το φως κινείται “μαζί” με τον αιθέρα, δηλαδή προς τη διεύθυνση του “αιθέριου ανέμου”, θα πρέπει να τρέχει λίγο γρηγορότερα απ’ ότι αν κινείται αντίθετα προς αυτόν. Και πάλι, το ανάλογο του κολυμβητή μας βοηθά στην κατανόηση: ο κολυμβητής προχωρά γρηγορότερα αν πάει σύμφωνα με το ρεύμα, παρά αν πάει αντίθετα προς αυτό.
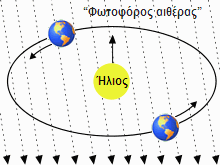
Τον “αιθέριο άνεμο” θα έπρεπε να τον αντιλαμβανόμαστε
λόγω την κίνησης της Γης εντός του “φωτοφόρου αιθέρα”
Ο Michelson απέτυχε στα πρώτα πειράματα. Το 1887 άρχισε να συνεργάζεται με τον Morley, οπότε μαζί έφτιαξαν μια συσκευή που ήταν κυκλική και έστελνε μια ακτίνα φωτός προς το κέντρο-της. Εκεί η ακτίνα χωριζόταν στα δύο, χάρη σε ένα “ημι-κάτοπτρο”, και οδηγείτο προς δύο άλλα κάτοπτρα στην περιφέρεια. Μετά από κάποιες διαδρομές στη συσκευή αυτή, που δεν είναι απαραίτητο να περιγραφούν με ακρίβεια εδώ, οι δύο ακτίνες φωτός έρχονταν στο ίδιο σημείο. Αν η ταχύτητα της ακτίνας που πήγαινε προς μία διεύθυνση ήταν — λόγω της κίνησης μέσα στον αιθέρα — ελαφρά διαφορετική από την ταχύτητα της άλλης ακτίνας (εκείνης που πήγαινε κάθετα προς την πρώτη), θα έπρεπε οι δύο ακτίνες να παρουσιάσουν φαινόμενο “μη συμβολής”.(*) Αλλά οι Michelson-Morley δεν παρατήρησαν τίποτε τέτοιο. Το φως φαινόταν να έχει την ίδια ταχύτητα προς οποιαδήποτε διεύθυνση, αγνοώντας τον αιθέρα!
Αντί όμως να συμπεράνουν οτι ίσως να μην υπάρχει ο αιθέρας, οι Michelson-Morley συμπέραναν οτι ίσως ο αιθέρας “παρασύρεται” από τη Γη, τουλάχιστον στην άμεση γειτονιά-της (π.χ. κοντά στην επιφάνειά της), και γιαυτό εμφανιζόμαστε σαν να είμαστε ακίνητοι ως προς τον αιθέρα. Το πείραμα των Michelson-Morley αργότερα ονομάστηκε “το πιο διάσημο αποτυχημένο πείραμα” στην ιστορία της φυσικής.
Σύντομα έγιναν και άλλα πειράματα από άλλους, που προσπάθησαν να βρουν τη διαφορά στην ταχύτητα του φωτός καθώς η Γη περιφέρεται γύρω από τον Ήλιο (βλ. και πάλι το προηγούμενο διάγραμμα). Και πάλι όμως, τα πειράματα αυτά απέτυχαν.
1.2 Το παράδοξο της ταχύτητας του φωτός
Τη σωστή υπόθεση, οτι δεν υπάρχει ο αιθέρας, την έκανε ο Αϊνστάιν αρκετά χρόνια αργότερα. Δεν είναι απολύτως βέβαιο αν ο Αϊνστάιν γνώριζε για το αποτυχημένο πείραμα των Michelson-Morley όταν ανέπτυσσε τη θεωρία που αργότερα ονομάστηκε “θεωρία της ειδικής σχετικότητας”. Άλλωστε το 1887 ο Αϊνστάιν ήταν μόλις 8 χρονών. Πάντως την εποχή που ο Αϊνστάιν ήταν νεαρός, οι φυσικοί διαπίστωναν το εξής εκπληκτικό: όσο γρήγορα και να κινείται ένας παρατηρητής που στέλνει μια ακτίνα φωτός π.χ. προς τα εμπρός (κατά τη διεύθυνση της κίνησής του), το φως θα έχει την ίδια ταχύτητα — αυτήν την ίδια ταχύτητα που γνωρίζουμε και σήμερα: c = 299.792.458 μέτρα το δευτερόλεπτο! (Ή, για να τη θυμόμαστε με έναν πιο στρογγυλό αριθμό: 300.000 χιλιόμετρα το δευτερόλεπτο.) Είτε ο κινούμενος παρατηρητής στείλει την ακτίνα φωτός προς τα εμπρός, είτε προς τα πίσω, το φως θα φύγει από αυτόν με την ίδια ταχύτητα, το c που σημειώσαμε προηγουμένως. Και μάλιστα, τόσο ο κινούμενος παρατηρητής (αυτός που στέλνει το φως π.χ., προς τη διεύθυνση της κίνησής του), όσο και ο ακίνητος παρατηρητής (που στέκεται στο έδαφος) θα μετρήσουν την ίδια τιμή, το c, για την ταχύτητα του φωτός! Ας σταματήσουμε μια στιγμή για να καταλάβουμε πόσο αντίθετο στην κοινή εμπειρία είναι αυτό.
Ας υποθέσουμε οτι είμαστε σε ένα
βαγόνι τρένου που κινείται με 100 χλμ. την ώρα. Παίρνουμε ένα μικρό
αντικείμενο, π.χ. ένα μπαλάκι του τένις, και το πετάμε μέσα στο βαγόνι
προς τα μπρος, δηλαδή προς την ίδια διεύθυνση που κινείται και το
τρένο, με ταχύτητα 5 χλμ/ώρα. (Είμαστε μόνοι-μας στο βαγόνι, και δεν
υπάρχει ελεγκτής για να μας κάνει παρατήρηση να μην πετάμε μπαλάκια!
![]() ) Με
πόση ταχύτητα θα δει να κινείται το μπαλάκι κάποιος που στέκεται έξω από
το βαγόνι, στο έδαφος; Απάντηση: με 105 χλμ/ώρα, γιατί το μπαλάκι θα
έχει τα 100 χλμ/ώρα του τρένου, συν τα 5 χλμ/ώρα με τα οποία το
πετάξαμε εμείς. Οι ταχύτητες θα προστεθούν. Αν, αντίθετα, το πετάξουμε
προς τα πίσω μέσα στο βαγόνι, και πάλι με 5 χλμ/ώρα, ο απ’ έξω
παρατηρητής θα το δει να κινείται με ταχύτητα 95 χλμ/ώρα ως προς το
έδαφος, γιατί οι ταχύτητες θα αφαιρεθούν: 100 – 5 = 95. Για μας,
μέσα στο βαγόνι, φυσικά το μπαλάκι θα κινείται με την ίδια ταχύτητα, 5
χλμ/ώρα ως προς το πάτωμα του βαγονιού, τόσο προς τη μια όσο και
προς την άλλη διεύθυνση, γιατί με την ίδια ταχύτητα το πετάμε. Αλλά για
τον εξωτερικό παρατηρητή, ως προς το έδαφος της Γης, το μπαλάκι έχει στη
μια περίπτωση 100 + 5 = 105 χλμ/ώρα, ενώ στην άλλη περίπτωση 100 – 5 =
95 χλμ/ώρα.
) Με
πόση ταχύτητα θα δει να κινείται το μπαλάκι κάποιος που στέκεται έξω από
το βαγόνι, στο έδαφος; Απάντηση: με 105 χλμ/ώρα, γιατί το μπαλάκι θα
έχει τα 100 χλμ/ώρα του τρένου, συν τα 5 χλμ/ώρα με τα οποία το
πετάξαμε εμείς. Οι ταχύτητες θα προστεθούν. Αν, αντίθετα, το πετάξουμε
προς τα πίσω μέσα στο βαγόνι, και πάλι με 5 χλμ/ώρα, ο απ’ έξω
παρατηρητής θα το δει να κινείται με ταχύτητα 95 χλμ/ώρα ως προς το
έδαφος, γιατί οι ταχύτητες θα αφαιρεθούν: 100 – 5 = 95. Για μας,
μέσα στο βαγόνι, φυσικά το μπαλάκι θα κινείται με την ίδια ταχύτητα, 5
χλμ/ώρα ως προς το πάτωμα του βαγονιού, τόσο προς τη μια όσο και
προς την άλλη διεύθυνση, γιατί με την ίδια ταχύτητα το πετάμε. Αλλά για
τον εξωτερικό παρατηρητή, ως προς το έδαφος της Γης, το μπαλάκι έχει στη
μια περίπτωση 100 + 5 = 105 χλμ/ώρα, ενώ στην άλλη περίπτωση 100 – 5 =
95 χλμ/ώρα.
Οι ταχύτητες λοιπόν προστίθενται ή αφαιρούνται — αυτό μας λέει η κοινή εμπειρία. Γιαυτό άλλωστε η “μετωπική σύγκρουση” των αυτοκινήτων είναι συχνά θανατηφόρα: αν τα δύο αυτοκίνητα που συγκρούονται μετωπικά έχουν, το ένα 110 χλμ/ώρα, και το άλλο 90 χλμ/ώρα, τότε κατά τη σύγκρουση είναι σαν ο κάθε οδηγός να πέφτει σε έναν τοίχο με ταχύτητα 110 + 90 = 200 χλμ/ώρα. Αντίθετα, αν τα αυτοκίνητα που συγκρούονται έχουν τις προαναφερθείσες ταχύτητες αλλά κινούνται προς την ίδια διεύθυνση, π.χ. το “πίσω” με 110 χλμ/ώρα και το “εμπρός” με 90 χλμ/ώρα, τότε η σύγκρουσή τους θα γίνει με μόλις 110 – 90 = 20 χλμ/ώρα· εδώ, οι ταχύτητες αφαιρούνται.
Όλα αυτά, λογικά και γνωστά. Νά όμως που τώρα μπαίνει το “παράλογο” όταν πρόκειται για το φως. Αν αντί για μπαλάκι του τένις στείλουμε προς τα μπρος και προς τα πίσω μια ακτίνα φωτός, τότε ο παρατηρητής που είναι ακίνητος στο έδαφος θα δει την ακτίνα να κινείται με την ίδια ταχύτητα, το c, και προς τις δύο διευθύνσεις! Ανεξάρτητα από την ταχύτητα του τρένου! Και ακριβώς την ίδια ταχύτητα, το c, θα μετρήσουμε και εμείς που είμαστε μέσα στο τρένο!
Καλά εμείς που είμαστε μέσα στο βαγόνι: εμείς “φυσιολογικά” (αναμενόμενα) θα παρατηρήσουμε την ίδια ταχύτητα, το c, ως προς το πάτωμα του βαγονιού. Άλλωστε το ίδιο είχαμε παρατηρήσει και με το μπαλάκι του τένις: 5 χλμ/ώρα και προς τα μπρος και προς τα πίσω. Ο παρατηρητής στο έδαφος όμως; Γιατί εκείνος να παρατηρεί την ταχύτητα c τόσο προς τα μπρος όσο και προς τα πίσω; Γιατί δεν προστίθεται το c στην ταχύτητα του τρένου όταν το φως στέλνεται προς τα μπρος, και δεν αφαιρείται από την ταχύτητα του τρένου όταν στέλνεται προς τα πίσω;
Κι αν το ίδιο το τρένο κινείται με ταχύτητα σχεδόν c (δεν λέμε ίση ή μεγαλύτερη — θα μάθουμε λίγο αργότερα γιατί), μήπως πάλι δεν θα προστεθούν οι ταχύτητες; Βεβαίως! Και πάλι, όταν πρόκειται για το φως, η ταχύτητα του φωτός εμφανίζεται σταθερή, πάντα ίση με c σχετικά με οποιονδήποτε παρατηρητή, ανεξάρτητα από το πόσο γρήγορα κινείται ο παρατηρητής, και ανεξάρτητα από το προς ποια διεύθυνση κινείται η πηγή του φωτός.
Και το εκπληκτικό, το αντίθετο στην κοινή εμπειρία που έχουμε με το μπαλάκι του τένις, είναι οτι καί ο κινούμενος, καί ο ακίνητος παρατηρητής, θα δουν το φως να κινείται με ταχύτητα c, ο καθένας ως προς τον εαυτό-του! Ας θυμηθούμε πόσο διαφορετικά είναι τα πράγματα με το μπαλάκι του τένις, που ο κινούμενος παρατηρητής το βλέπει να κινείται με ταχύτητα 5 χλμ/ώρα ως προς τον εαυτό-του, ενώ ο ακίνητος το βλέπει να κινείται με 105 ή 95 χλμ/ώρα ως προς τον εαυτό-του, ανάλογα με τη διεύθυνση της κίνησης. Πώς γίνεται το φως να κινείται με ταχύτητα c ως προς οποιονδήποτε παρατηρητή;
|
Η ταχύτητα του φωτός φαίνεται να είναι μια “σταθερά” του σύμπαντος. |
Εδώ ίσως θα αναρωτηθεί ο αναγνώστης: «Μα καλά, πώς το ξέρουμε οτι ισχύει αυτό; Γιατί να είναι αλήθεια; Ποιος μας το εγγυάται;»
Μας το εγγυώνται εκατοντάδες, χιλιάδες πειράματα! Όταν παρατηρούμε τη φύση, βλέπουμε οτι έτσι είναι: η ταχύτητα του φωτός είναι σταθερή, ανεξάρτητη από την ταχύτητα της πηγής-της. Μπορεί η πηγή του φωτός να τρέχει πολύ γρήγορα, όσο πιο γρήγορα μπορεί· όσο και να προσπαθήσει όμως, δεν θα καταφέρει ποτέ να κάνει το φως να τρέξει πιο γρήγορα από c. Αυτό λοιπόν το γεγονός μας το πληροφορούν οι παρατηρήσεις, τα πειράματα. Πρόκειται για ένα δεδομένο, που προκύπτει κατευθείαν από την παρατήρηση.
Άλλωστε και το αποτυχημένο πείραμα των Michelson και Morley ήταν μια ένδειξη για τη σταθερότητα της ταχύτητας του φωτός. Το πείραμά τους έδειξε οτι η ταχύτητα του φωτός είναι σταθερή προς οποιαδήποτε διεύθυνση, οτι το φως δεν “παρασέρνεται” από τον αιθέρα, αν υπήρχε αιθέρας. Μόνο που ούτε ο Michelson, ούτε ο Morley, ούτε οι άλλοι φυσικοί της εποχής εκείνης που έμαθαν για το πείραμά τους το ερμήνευσαν σωστά.
Πρέπει τώρα λοιπόν να δούμε ποιες είναι οι συνέπειες της “παραξενιάς” αυτής με το c: τη σταθερότητα της ταχύτητας του φωτός.
1.3 Πώς γίνεται η πρόσθεση των ταχυτήτων
Όπως είπαμε, αν ο παρατηρητής που είναι μέσα στο τρένο ρίξει το μπαλάκι του τένις με 5 χλμ/ώρα προς την ίδια διεύθυνση που το τρένο κινείται με 100 χλμ/ώρα, τότε εμείς απ’ έξω, αν είμαστε ακίνητοι στο έδαφος, θα δούμε το μπαλάκι να κινείται με 5 + 100 = 105 χλμ/ώρα.
Αν όμως ο παρατηρητής που κινείται με το τρένο ρίξει μια ακτίνα φωτός (φωτόνια) από το φακό-του αντί για το μπαλάκι, τότε εμείς απ’ έξω δεν θα δούμε την ακτίνα φωτός να κινείται με c + 100 χλμ/ώρα (ας υποθέσουμε οτι εκφράσαμε το c σε χλμ/ώρα, ώστε να συμφωνούν οι μονάδες μέτρησης), αλλά πάλι με c χλμ/ώρα. Το φως δεν θα κινηθεί “ταχύτερα απ’ το φως”!
Πώς γίνεται να διαφωνούν τόσο ριζικά τα δύο παρόμοια πειράματα; Μήπως στην πρώτη περίπτωση, με το μπαλάκι του τένις, το αποτέλεσμα δεν είναι ακριβώς 105 χλμ/ώρα, αλλά κάτι λιγότερο;
Πράγματι, αυτό συμβαίνει. Αυτό που νομίζουμε οτι είναι η πρόσθεση των ταχυτήτων, δεν είναι ακριβώς η γνωστή-μας πρόσθεση, αλλά κάτι λιγότερο. Μονάχα που αυτό το “κάτι λιγότερο” είναι τόσο μικρό όταν πρόκειται για μπαλάκια του τένις και τρένα, που εμείς οι άνθρωποι, για να αντιληφθούμε τη διαφορά, χρειαζόμαστε τόσο ακριβή τεχνικά μέσα μέτρησης μήκους και χρόνου, που είναι αδύνατο να κατασκευάσουμε με την τρέχουσα τεχνολογία. Ας δούμε πόση είναι αυτή η διαφορά, αυτό το “κάτι λιγότερο”.
Ας πούμε v1 την ταχύτητα του τρένου (ώστε να μη χρησιμοποιούμε σταθερούς αριθμούς όπως το 100, ούτε συγκεκριμένες μονάδες όπως το χλμ/ώρα), και v2 την ταχύτητα του “άλλου πράγματος” που ρίχνεται προς τα μπρος μέσα στο τρένο, είτε είναι αυτό μπαλάκι του τένις, είτε φωτόνια (ακτίνα φωτός).
Τότε η κλασική φυσική, αυτή που θεμελίωσε ο Νεύτωνας το 17ο αιώνα, λέει οτι ο παρατηρητής που είναι έξω στο έδαφος, ακίνητος, θα παρατηρήσει οτι το αντικείμενο που “ρίχτηκε” προς τα μπρος κινείται με ταχύτητα v ίση με το απλό άθροισμα των δύο ταχυτήτων:
v = v1 + v2
Σύμφωνα με τη θεωρία της ειδικής σχετικότητας όμως, που θεμελίωσε ο Αϊνστάιν και πρωτοδιατύπωσε το 1905, ο τύπος για την ταχύτητα v είναι λίγο πιο πολύπλοκος. Είναι ο εξής:
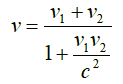
Όπως βλέπουμε, ο σχετικιστικός τύπος για το “άθροισμα ταχυτήτων” δεν είναι καθόλου πολύπλοκος από μαθηματική άποψη· χρησιμοποιεί μόνο κλάσματα, πρόσθεση, πολλαπλασιασμό, και έχει την ταχύτητα του φωτός c στο τετράγωνο.
Ας δούμε όμως τί σημαίνει αυτός ο τύπος. Ας υπολογίσουμε τώρα το άθροισμα των ταχυτήτων όταν έχουμε να κάνουμε με το τρένο (v1 = 100 χλμ/ώρα), και το μπαλάκι του τένις (v2 = 5 χλμ/ώρα), κινούμενα και τα δύο προς την ίδια διεύθυνση. Αντικαθιστώντας τις τιμές των v1 και v2 στο σχετικιστικό τύπο, παίρνουμε:
v = (100 + 5) / (1 + 100·5 / c 2 )
Για να κάνουμε τις πράξεις, πρέπει βέβαια να εκφράσουμε το c σε χλμ/ώρα, για να ταιριάζουν οι μονάδες (να μη συγκρίνουμε «μήλα με πορτοκάλια», όπως μας έλεγαν στο δημοτικό). Η τιμή του c είναι, όπως είπαμε, 299.792.458 μέτρα το δευτερόλεπτο. Άρα είναι 299.792,458 χιλιόμετρα το δευτερόλεπτο (προσέξτε πού μπήκε η υποδιαστολή, αφού διαιρέσαμε διά 1000). Άρα, καθώς η ώρα έχει 3600 δευτερόλεπτα, πολλαπλασιάζοντας τον προηγούμενο αριθμό επί 3600, παίρνουμε: c = 1.079.252.848,8 χλμ/ώρα. Ολογράφως: ένα δισεκατομμύριο, 79 εκατομμύρια... χλμ/ώρα, λέει αυτός ο αριθμός!
Παρεμπιπτόντως, έχει σημασία να καταλάβουμε ποιες είναι οι ταχύτητες των γρηγορότερων αντικειμένων που φτιάχνει ο άνθρωπος. Αν νομίζατε οτι ένα αυτοκίνητο που κινείται με 200 χλμ/ώρα «τρέχει σαν σφαίρα», τότε σκεφτείτε τί σημαίνει το 1 δισεκατομμύριο χλμ/ώρα. Και, αν επίσης νομίζατε, οτι μια πραγματική σφαίρα είναι το γρηγορότερα κινούμενο πράγμα στον κόσμο (λέγεται αυτό μερικές φορές, από ανθρώπους όχι καλά πληροφορημένους), θα πρέπει να αναθεωρήσετε· η ταχύτητα της σφαίρας δεν ξεπερνάει τα 1200 μέτρα/δευτερόλεπτο στα πιο μοντέρνα τουφέκια (πηγή, Wikipedia, στα αγγλικά), δηλαδή τα 4320 χλμ/ώρα. Το γρηγορότερα κινούμενο αεροπλάνο εντός της ατμόσφαιρας του πλανήτη-μας που πιλοτάρεται από άνθρωπο, την εποχή που γράφτηκε το παρόν, είναι το αμερικανικό στρατιωτικό υπερηχητικό τζετ Lockheed SR-71 Blackbird, που φτάνει σε ταχύτητα τα 3,3–3,5 mach, δηλαδή (το πολύ) 3,5 φορές την ταχύτητα του ήχου στον αέρα, ήτοι τα 4322 χλμ/ώρα (κατά σύμπτωση ίδια ταχύτητα με εκείνη της γρηγορότερης σφαίρας!)· ενώ οι πύραυλοι, που βέβαια δεν μεταφέρουν πιλότο, κινούνται ακόμα ταχύτερα, φτάνοντας τα 21.000 χλμ/ώρα (πηγή). Πιο γρήγορα ακόμα είναι τα διαστημόπλοια, καθώς δεν έχουν να αντιμετωπίσουν την αντίσταση του αέρα. Το ρεκόρ με αστροναύτες είναι 39.897 χλμ/ώρα από το Apollo 10 (πηγή, καταγράφεται και στα ρεκόρ Γκίνες), που έφτασε στη Σελήνη, μπήκε σε τροχιά, αλλά δεν προσσεληνώθηκε κ’ επέστρεψε στη Γη (ήταν η “πρόβα τζενεράλε” πριν από την αποστολή του Apollo 11, που προσσεληνώθηκε). Μη επανδρωμένα σύγχρονα διαστημόπλοια φτάνουν σε ακόμα μεγαλύτερες ταχύτητες ως προς τη Γη, πλησιάζοντας τα 60.000 χλμ/ώρα (πηγή).
Όλες αυτές όμως οι ταχύτητες, ακόμα και των 60.000 χλμ/ώρα, ωχριούν μπροστά στο 1 δισεκατομμύριο του φωτός. Και αυτό — ας το επαναλάβουμε — είναι πολύ σημαντικό να το θυμόμαστε όταν θα έρθει η ώρα να καταλάβουμε για ποιο λόγο η ανθρώπινη νοημοσύνη αντιλαμβάνεται τον κόσμο “παραμορφωμένο”, δηλ. με την κλασική Ευκλείδεια/Γαλιλαιική γεωμετρία, και όχι με τη σχετικιστική. Αντιλαμβανόμαστε τον κόσμο με την κλασική φυσική του Νεύτωνα, και όχι με τη σχετικιστική φυσική του Αϊνστάιν, και ο λόγος είναι αυτές οι απελπιστικά αργές (ως προς το φως) ταχύτητες του περιβάλλοντός μας, όπως θα διαπιστώσουμε.
Ας επιστρέψουμε όμως στον υπολογισμό του v μέσω του σχετικιστικού τύπου v = (100 + 5) / (1 + 100·5 / c2). Εδώ λοιπόν πρέπει να υψώσουμε το c, δηλαδή το 1 δισεκατομμύριο, στο τετράγωνο. Αυτό, δηλ. το c2, είναι ο αριθμός: 1.164.786.711.642.915.661,44 (ένα πεντάκις εκατομμύριο, “και κάτι ψιλά”). Άρα πρέπει να διαιρέσουμε τον αριθμό 100·5, δηλ. το 500, διά αυτού του “αστρονομικού” αριθμού. Το αποτέλεσμα είναι 0,000000000000000429 “και κάτι ψιλά”. Προσθέτοντας αυτόν τον εξαιρετικά μικρό αριθμό στο 1 (είμαστε στον παρονομαστή του τύπου ακόμα), έχουμε 1,000000000000000429. Αυτός είναι ο παρονομαστής. Επομένως πρέπει να διαιρέσουμε το (100 + 5) διά αυτού του αριθμού. Έτσι, αντί για 105 (χλμ/ώρα) παίρνουμε: 104,9999999999999549 χλμ/ώρα.
Συμπέρασμα: το μπαλάκι του τένις, όπως το βλέπουμε από το έδαφος, δεν τρέχει με 105, αλλά με 104,9999999999999549 χλμ/ώρα.
Ποιος όμως μπορεί να μετρήσει μια τέτοια απειροελάχιστη διαφορά από το 105;
Κανείς, με τα σύγχρονα μέσα. Όταν η διαφορά από το 105 είναι στο 14ο δεκαδικό ψηφίο, δεν πρέπει να μας κάνει καμία εντύπωση οτι κανείς, μέχρι την εποχή του Αϊνστάιν, δεν μπορούσε να αντιληφθεί οτι το άθροισμα των ταχυτήτων δεν είναι ακριβώς το v1 + v2, αλλά το (v1 + v2) / (1 + v1·v2 / c2).
Ο σχετικιστικός τύπος μας λέει οτι όταν οι ταχύτητες είναι μικρές, όπως τα 100 χλμ/ώρα του τρένου και τα 5 χλμ/ώρα της μπάλας του τένις, τότε η διαφορά από το “πλήρες” v1 + v2 είναι “αστρονομικά” μικρή.
Τί γίνεται όμως όταν οι ταχύτητες είναι μεγάλες; Τί γίνεται αν το “τρένο” (σκεφτείτε διαστημόπλοιο επιστημονικής φαντασίας) τρέχει με ταχύτητα σχεδόν ίση με την ταχύτητα του φωτός; (Όπως είπαμε, και θα δούμε το γιατί, την ταχύτητα του φωτός δεν μπορούμε να την “πιάσουμε”, πόσω μάλλον να την ξεπεράσουμε, ξεκινώντας από την ακινησία.) Τί θα παρατηρήσουμε εμείς ως παρατηρητές του εδάφους όταν σε ένα τέτοιο “διαστημικό τρένο” ένας επιβάτης εκτοξεύσει προς τα εμπρός ένα βλήμα που κι αυτό τρέχει σχεδόν με c;
Τώρα λοιπόν, αντί για 5 χλμ/ώρα έχουμε το “σχεδόν c”. Και αντί για τα 100 χλμ/ώρα έχουμε πάλι το “σχεδόν c”. Ας τα εξισώσουμε αυτά τα “σχεδόν c” ακριβώς με το c, για να απλοποιήσουμε το αποτέλεσμα. Βάζουμε λοιπόν όπου v1 το c, και όπου v2 πάλι το c στο σχετικιστικό τύπο. Οπότε παίρνουμε: v = (c + c) / (1 + c·c / c2). Αυτό μας κάνει: v = (2c) / (1 + c2 / c2). Δηλαδή: v = 2c / (1 + 1). Άρα v = 2c / 2. Άρα, τελικά: v = c. Βρήκαμε δηλαδή οτι η τελική ταχύτητα θα είναι πάλι το c! Που σημαίνει πως, ενώ ο παρατηρητής εντός του διαστημικά κινούμενου τρένου εκτοξεύει το βλήμα σχεδόν με την ταχύτητα του φωτός c, και ενώ το τρένο-του τρέχει κι αυτό σχεδόν με την ίδια ταχύτητα, εμείς απ’ έξω βλέπουμε το “προωθημένο βλήμα” να κινείται πάλι το πολύ με c, κι όχι παραπάνω. Δεν “προωθείται” το βλήμα για να τρέξει ακόμα πιο γρήγορα από το φως — αυτό είναι το συμπέρασμα από το σχετικιστικό τύπο.
Βέβαια αν το βλήμα κινείται προς την αντίθετη διεύθυνση από αυτήν της κίνησης του τρένου, αρκεί να αλλάξουμε το + σε – στον αριθμητή του τύπου, δηλαδή να γράψουμε τον τύπο έτσι: v = (v1 – v2) / (1 + v1·v2 / c2), για να βρούμε σωστά αποτελέσματα.
Ίσως εδώ ο αναγνώστης να αναρωτηθεί: «Μα αξίζει τον κόπο να τα γνωρίζουμε όλα αυτά, αφού για να παρατηρήσουμε σημαντικές αποκλίσεις από τις προβλέψεις της κλασικής φυσικής απαιτούνται ταχύτητες που είναι συγκρίσιμες με την ταχύτητα του φωτός, και δεν υπάρχουν τέτοιες ταχύτητες στο περιβάλλον-μας; Αφού ακόμα και οι ταχύτητες των διαστημοπλοίων σήμερα ωχριούν μπροστά στην ταχύτητα του φωτός, όπως αναφέρθηκε παραπάνω;»
Και όμως, πλέον υπάρχουν και ταχύτητες κοντά στην ταχύτητα του φωτός, με τις οποίες ασχολούμαστε εμείς οι άνθρωποι. Πρόκειται για τις ταχύτητες των σωματιδίων στους επιταχυντές στοιχειωδών σωματιδίων, που είναι τα “μικροσκόπια” (ας τους πούμε έτσι) των πυρηνικών φυσικών. Μέσω των επιταχυντών βγάζουμε πολύτιμα συμπεράσματα για τη δομή της ύλης, χωρίς τα οποία δεν θα μπορούσαμε να έχουμε μια πειστική θεωρία κβαντομηχανικής. Και χωρίς αυτή, δεν θα υπήρχαν οι ημιαγωγοί, για να πάρουμε ένα παράδειγμα, χάρη στους οποίους φτιάχνονται οι υπολογιστές. Άρα δεν θα είχαμε ούτε κινητά τηλέφωνα, ούτε διαδίκτυο, ούτε καν τηλεοράσεις υψηλής τεχνολογίας. Χωρίς τη θεωρία της σχετικότητας, η συμπεριφορά των κβαντικών σωματιδίων στις υψηλές ταχύτητες (που πλησιάζουν κατά πολύ την ταχύτητα του φωτός) θα ήταν ακατανόητη, άρα δεν θα μπορούσαμε να κατασκευάζουμε μηχανήματα που σήμερα κατασκευάζουμε γιατί τα κατανοούμε. Χωρίς τη σχετικότητα, η ανθρώπινη τεχνολογία μάλλον θα βρισκόταν ακόμη στην προ του 2ου Παγκοσμίου Πολέμου εποχή.
Ας συνοψίσουμε τώρα το βασικό συμπέρασμα που μάθαμε στην παρούσα υποενότητα:
|
Α Σ Υ Μ Φ Ω Ν Ι Α Α Π Ο Ψ Ε Ω Ν: Τ Ο Α Θ Ρ Ο Ι Σ Μ Α Τ Α Χ Υ Τ Η Τ Ω Ν |
|||||
| Η Κ Λ Α Σ Ι Κ Η Α Π Ο Ψ Η | Η Σ Χ Ε Τ Ι Κ Ι Σ Τ Ι Κ Η Α Π Ο Ψ Η | ||||
|
|
||||
Παρόλο που αναφερόμαστε σε “απόψεις” στην επικεφαλίδα του παραπάνω πίνακα, ας σημειωθεί οτι δεν πρόκειται για απλές απόψεις των δύο επιστημόνων που εικονίζονται (Νεύτων – Αϊνστάιν). Η σχετικιστική άποψη έχει επιβεβαιωθεί πως είναι η πιο σωστή μέσω αμέτρητων πειραμάτων, που συνεχίζουν να πραγματοποιούνται ακόμη κι αν δεν έχουν σκοπό σήμερα να επιβεβαιώσουν τον τύπο του αθροίσματος ταχυτήτων, όπως συμβαίνει π.χ. στους επιταχυντές στοιχειωδών σωματιδίων.
Και μια παρένθεση ακόμη: ίσως αναρωτηθεί ο αναγνώστης, για ποιο λόγο, σ’ αυτό και σε παρόμοια πινακάκια που θα ακολουθήσουν, απεικονίζεται ο Νεύτωνας ως ο εκπρόσωπος της κλασικής άποψης, εφόσον η τελευταία εξέφραζε χιλιάδες επιστήμονες από την εποχή του Γαλιλαίου (που πέθανε τη χρονιά που γεννήθηκε ο Νεύτωνας) μέχρι την εποχή του Αϊνστάιν. Ο λόγος είναι οτι ο Νεύτων ήταν ο “θεμελιωτής” της κλασικής φυσικής. Όπως μαθαίνουμε στο μάθημα Ε2, μπορεί ο Γαλιλαίος να υπήρξε ο “ιδρυτής”, αλλά ο Νεύτωνας θεμελίωσε μαθηματικά την κλασική φυσική. Επιπλέον, υπήρξε και ο θεμελιωτής ενός από τους σπουδαιότερους κλάδους των μαθηματικών: του απειροστικού λογισμού. Έχοντας λοιπόν βάλει τα θεμέλια τόσο για τα σύγχρονα μαθηματικά, όσο και για την κλασική φυσική, δεν θα ήταν υπερβολή να πούμε οτι ο Νεύτων διεκδικεί τον τίτλο του “σημαντικότερου επιστήμονα όλων των εποχών”, που η συμβολή-του στην επιστήμη είναι μάλλον πιο θεμελιώδης από του Αϊνστάιν, με περισσότερο εύρος και επιπτώσεις στην καθημερινότητά μας, μπορούμε να πούμε. Αντίθετα, για τη δεξιά στήλη του πίνακα, κανένας άλλος επιστήμονας δεν υπάρχει που να μπορεί να διεκδικήσει μια θέση στη θεωρία της σχετικότητας εφάμιλλη με αυτή του Αϊνστάιν.(*) Για τη σχετικότητα, μπορούμε να πούμε οτι ο Αϊνστάιν «τα είπε όλα».
1.4 Το παράδοξο της διαστολής του χρόνου
Στην προηγούμενη υποενότητα είδαμε οτι δεν μπορούμε, προσθέτοντας ταχύτητες, να ξεπεράσουμε την ταχύτητα του φωτός. Αυτό το διαπιστώσαμε όταν στο σχετικιστικό τύπο του αθροίσματος βάλαμε όπου v1 το c, και όπου v2 πάλι το c, και βρήκαμε οτι το “άθροισμα” (δηλαδή το αποτέλεσμα του τύπου) ήταν πάλι c. Άρα η παράξενη αυτή “σχετικιστική πρόσθεση” μας δίνει: c + c = c. Δηλαδή και δύο φορές να βάλουμε την ταχύτητα του φωτός, δεν θα πάρουμε περισσότερο από μία φορά την ταχύτητα του φωτός!
Μπορούμε ακόμα, σαν άσκηση, να βάλουμε στον τύπο όπου v1 το c, και όπου v2 ένα οποιοδήποτε v < c, δηλαδή μια οποιαδήποτε ταχύτητα μικρότερη της ταχύτητας του φωτός. Και πάλι, το αποτέλεσμα θα είναι c. (Ο αναγνώστης που έχει το απαραίτητο υπόβαθρο στη γυμνασιακή άλγεβρα μπορεί, σαν άσκηση, να κάνει τις πράξεις και να το δει.) Όλες αυτές οι προσπάθειες μας λένε οτι:
|
Δεν είναι δυνατόν, προσθέτοντας ταχύτητες μικρότερες ή ίσες με την ταχύτητα του φωτός, να ξεπεράσουμε την ταχύτητα του φωτός. |
Αλλά τώρα θα φανταστούμε κάτι το παράδοξο, κάτι που θα μοιάζει να αντιτίθεται σ’ αυτό που βάλαμε στο παραπάνω πλαίσιο. (Κάθε τέτοια φανταστική κατάσταση ονομάζεται “πείραμα σκέψης” — αγγλ.: “thought experiment”. Ο Αϊνστάιν είναι γνωστό οτι ανέπτυξε τη θεωρία της σχετικότητας κάνοντας τέτοια “πειράματα σκέψης”, και ο όρος αυτός υπάρχει και χρησιμοποιείται από τότε.)
Ας φανταστούμε ένα διαστημόπλοιο που κινείται με ταχύτητα τόσο μεγάλη, που υπολείπεται κατά 1 μόνο χλμ/ώρα της ταχύτητας του φωτός. Εφόσον λοιπόν το c = 1.079.252.848,8 χλμ/ώρα (όπως είχαμε βρει στην §1.3), το διαστημόπλοιο έχει την εξής απίστευτα μεγάλη ταχύτητα: v = 1.079.252.847,8 χλμ/ώρα (μόνο το τελευταίο ψηφίο πριν από την υποδιαστολή διαφέρει από το c). Εμείς στεκόμαστε ακίνητοι στη Γη, και παρατηρούμε το διαστημόπλοιο αυτό. (Θα υποθέσουμε ελαφρώς “υπεράνθρωπες” ικανότητες παρατήρησης, δηλαδή θα μπορούμε να βλέπουμε με ένα “υπερτηλεσκόπιο” τί γίνεται μέσα στο διαστημόπλοιο αυτό, παρόλο που θα είμαστε στη Γη. Στα πειράματα σκέψης επιτρέπονται πράγματα που είναι αδύνατα για την τρέχουσα τεχνολογία.)
Μέσα στο διαστημόπλοιο βρίσκεται ένας παρατηρητής, ο Β. (Εμείς έχουμε την κωδική ονομασία “Α”.) Βλέπουμε τον Β να κάθεται, άρα φυσικά κινείται μαζί με το διαστημόπλοιο με ταχύτητα v ως προς εμάς, που η v είναι κατά ένα χλμ/ώρα μικρότερη από το c. Ο Β είναι λοιπόν ακίνητος ως προς το πάτωμα του διαστημοπλοίου.
Ξαφνικά ο Β σηκώνεται από τη θέση-του, και αρχίζει να βαδίζει μέσα στο διάδρομο του θαλάμου του διαστημοπλοίου, κανονικά, “προς τα μπρος”, δηλαδή κατά την ίδια διεύθυνση της κίνησης του διαστημοπλοίου. Λέγοντας “κανονικά” εννοούμε πως βαδίζει με τη συνήθη ταχύτητα που έχουμε όταν βαδίζουμε. Αυτή είναι γύρω στα 6 χλμ/ώρα για έναν ενήλικο. Βλέπουμε το διαστημόπλοιο να κινείται με v, και μέσα-του τον Β να περπατάει με 6 χλμ/ώρα.
Μα πώς είναι δυνατόν αυτό; Αν προσθέσουμε το v και το 6, θα πάρουμε έναν αριθμό μεγαλύτερο από c, αφού c – v = 1. Θα πείτε, πρέπει να κάνουμε σχετικιστική πρόσθεση, να εφαρμόσουμε τον τύπο που μάθαμε για το άθροισμα ταχυτήτων, και το πλαίσιο που μόλις είδαμε μας λέει οτι έτσι δεν πρόκειται να ξεπεράσουμε την ταχύτητα του φωτός. Ναι, αλλά εμείς βλέπουμε το διαστημόπλοιο να κινείται με v, και βλέπουμε τον Β να περπατάει με 6 χλμ/ώρα ως προς το πάτωμα του διαστημοπλοίου! Τί εμποδίζει τον Β από του να περπατήσει κανονικά, με την ταχύτητα του βαδίσματος, πάνω στο πάτωμα του διαστημοπλοίου; Εφόσον βλέπουμε το πάτωμα να κινείται με v, και τον Β να περπατάει πάνω σ’ αυτό με 6 χλμ/ώρα, δεν έπεται άραγε οτι θα βλέπουμε τον Β να κινείται με 6 χλμ/ώρα παραπάνω από το v; Δηλαδή με ταχύτητα “υπερφωτική” (“superluminal”) όπως λέγονται αυτές οι ταχύτητες; Πού βρίσκεται το λάθος;
Αν αυτό που γράφει το προηγούμενο πλαίσιο είναι αλήθεια και ισχύει (και αν δεν ίσχυε, μάλλον δεν θα το βάζαμε σε πλαίσιο!), τότε τί μπορεί να συμβεί; Τί μπορεί να εμποδίσει τον Β από του να σηκωθεί και να περπατήσει κανονικά; Μήπως ένα “αόρατο χέρι”, το “χέρι του σύμπαντος” που δεν επιτρέπει υπερφωτικές ταχύτητες να συμβούν, θα εμποδίσει τον Β να προχωρήσει κανονικά; Ή, για να κάνουμε το πράγμα λιγότερο υπερφυσικό, μήπως ο Β θα νιώσει κάποια αντίσταση, όπως νιώθουμε όταν θέλουμε να βαδίσουμε προς τα μπρος σε ένα βαγόνι που επιταχύνει;
Όχι, τίποτα τέτοιο δεν θα συμβεί. Θα συμβεί κάτι άλλο, ακόμα πιο παράδοξο!
Αυτός ο άνθρωπος, ο Β, καθ’ όλη τη διάρκεια του ταξιδιού, δεν θα συμπεριφέρεται όπως συμπεριφέρονται συνήθως οι άνθρωποι. Θα μας φαίνεται πολύ... αργός! Εξαιρετικά αργός!
Όταν λέμε «αργός», το εννοούμε στην κυριολεξία. Όχι μόνο οι κινήσεις-του, αλλά και ο καρδιακός-του ρυθμός θα είναι εξαιρετικά αργός. Και οι σκέψεις-του ακόμα! (Θα δούμε αμέσως παρακάτω μια από τις πειραματικές επιβεβαιώσεις που μας δείχνουν οτι όλα αυτά είναι σωστά, και όχι σενάριο επιστημονικής φαντασίας.) Τα πάντα, στο σώμα του Β, και μέσα στο περιβάλλον του στο θάλαμο του διαστημοπλοίου, θα συμβαίνουν εξαιρετικά αργά. Και τα μόρια των υλικών του θαλάμου ακόμα, θα πάλλονται εξαιρετικά αργά. Ο χρόνος θα είναι σαν να έχει σχεδόν σταματήσει!
Ο ίδιος ο Β όμως, δεν θα αισθάνεται καθόλου “αργός”. Για εκείνον, όλα θα βαίνουν ομαλά. Και οι σκέψεις-του θα φαίνονται στον ίδιον οτι λειτουργούν με το συνηθισμένο ρυθμό, και τα αντικείμενα στο θάλαμο θα κινούνται κανονικά. Π.χ. αν πάρει ένα ποτήρι και το αφήσει να πέσει, αυτό θα κινηθεί κανονικά προς το πάτωμα (υποθέτουμε ένα είδος τεχνητής βαρύτητας στο διαστημόπλοιο, που δεν είναι κάτι ανέφικτο ακόμα και με τη σημερινή τεχνολογία — π.χ. μέσω περιστροφικής κίνησης). Το ποτήρι θα σπάσει κανονικά στο πάτωμα, και τα θρύψαλα του γυαλιού θα σκορπιστούν με τις αναμενόμενες ταχύτητες. Έτσι θα βλέπει τα πράγματα ο Β. Εμείς όμως, στη θέση του Α, με το υπερτηλεσκόπιό μας, θα βλέπουμε τα πάντα σε εξαιρετικά αργή κίνηση! Τί συμβαίνει;
Συμβαίνει οτι ο χρόνος δεν είναι κάτι το αναλλοίωτο για όλους. Ο ρυθμός με τον οποίο κυλά ο χρόνος εξαρτάται από την κίνηση του συστήματος μέσα στο χώρο. Όσο πιο μεγάλη είναι η ταχύτητα του συστήματος (μεγάλη σε σύγκριση με το c), τόσο πιο αργός είναι ο ρυθμός του χρόνου στο σύστημα αυτό.
Οπότε, για να απαντήσουμε το αρχικό πείραμα σκέψης, μπορεί μεν ο Β να σηκωθεί και να περπατήσει μέσα στο διαστημόπλοιο, αλλά αυτό δεν θα γίνει “ξαφνικά” όπως θα τον βλέπουμε εμείς. Θα γίνει πολύ-πολύ αργά. Ο ίδιος ο Β όμως δεν θα έχει αυτή την εντύπωση. Εκείνος θα νομίζει οτι σηκώθηκε ξαφνικά και περπατάει κανονικά, με ταχύτητα 6 χλμ/ώρα. Εμείς όμως θα βλέπουμε μια ταχύτητα εξαιρετικά αργή, τόσο αργή, τόσο πολύ μικρότερη από 6 χλμ/ώρα, κι ακόμα κι από το 1 χλμ/ώρα που είναι η διαφορά c – v, που δεν θα αξίζει καν τον κόπο να την προσθέσουμε στο c για να δούμε μήπως το τελευταίο ξεπεραστεί — που δεν θα ξεπεραστεί.
Βέβαια, για σώματα που κινούνται στο συνηθισμένο περιβάλλον-μας, με τις ταχύτητες που είναι εξαιρετικά αργές σε σύγκριση με το c, η καθυστέρηση στο ρυθμό του χρόνου είναι απειροελάχιστη, πέρα από κάθε τεχνολογική δυνατότητά μας να την ανιχνεύσουμε. Ας θυμηθούμε το παράδειγμα της §1.3, όπου υπολογίσαμε οτι το μπαλάκι του τένις στο τρένο κινείται με 104,9999999999999549 αντί για 105 χλμ/ώρα. (Πρόκειται για διαφορά στο ρυθμό του χρόνου, αυτό είναι που προκαλεί τη διαφορετική ταχύτητα.) Κανείς δεν μπορεί να αντιληφθεί, ή και να μετρήσει ακόμα, μια τέτοια διαφορά, γιαυτό και οι κλασικοί φυσικοί υπέθεταν οτι η ταχύτητα της μπάλας στο παράδειγμά μας είναι ακριβώς 105 χλμ/ώρα· διότι όλες οι ταχύτητες με τις οποίες ασχολήθηκαν ποτέ, από τα αρχαία χρόνια μέχρι την εποχή του Αϊνστάιν, ήσαν εξαιρετικά αργές ως προς το c. Εκεί όμως, λίγο πριν την εποχή του Αϊνστάιν, οι άνθρωποι άρχισαν να πειραματίζονται με την ταχύτητα του φωτός, και τότε τα δεδομένα άλλαξαν. Τα πειράματά τους άρχισαν να δείχνουν τη διαφορά στη ροή του χρόνου. Και ο πρώτος που το κατάλαβε αυτό ήταν ο Αϊνστάιν.
Ας βάλουμε λοιπόν αυτή την “ασυμφωνία απόψεων” σε ένα πλαισιο:
|
Α Σ Υ Μ Φ Ω Ν Ι Α Α Π Ο Ψ Ε Ω Ν: Η Ρ Ο Η Τ Ο Υ Χ Ρ Ο Ν Ο Υ |
|||||
| Η Κ Λ Α Σ Ι Κ Η Α Π Ο Ψ Η | Η Σ Χ Ε Τ Ι Κ Ι Σ Τ Ι Κ Η Α Π Ο Ψ Η | ||||
|
|
||||
Τώρα, η αλήθεια είναι οτι ένας αναγνώστης που ήδη γνωρίζει αρκετά περί θεωρίας της σχετικότητας, μπορεί να παραξενευτεί από την “απολυτότητα” με την οποία παρουσιάσαμε ως τώρα τη “σχετικότητα”· πράγμα που δημιουργεί αντίφαση (απόλυτο – σχετικό). Συγκεκριμένα, είπαμε οτι ο χρόνος στο διαστημόπλοιο του Β θα ρέει πιο αργά όπως τον παρατηρεί ο Α. Και είπαμε οτι ο Α είναι «ακίνητος»· σαν να είναι απολύτως ακίνητος, σαν να υπάρχει κάποιο σημείο στο σύμπαν όπου μπορούμε να σταθούμε ακίνητοι. Μα κι ο Β, αν πάρει εκείνος το υπερτηλεσκόπιό του και παρατηρήσει τον Α, θα δει τον Α να κινείται με ταχύτητα v ως προς τον Β· άρα, δεν θα πρέπει κι ο Β να βλέπει το χρόνο του Α να ρέει πολύ αργά; Και στο υποτιθέμενο αντεπιχείρημα οτι ο Α είναι στη Γη, ενώ ο Β σε διαστημόπλοιο, που “προφανώς” κινείται, θα μπορούσαμε να τους βάλουμε καί τους δυο σε διαστημόπλοια, τον καθένα σε άλλο διαστημόπλοιο φυσικά, και να βρίσκονται μακριά από όλους τους πλανήτες και όλα τα άστρα — π.χ. στο διαγαλαξιακό χώρο. Οπότε τώρα, ποιος κινείται και ποιος μένει ακίνητος; (Εξ ου και “σχετικότητα”, η σχετικότητα της κίνησης.)
Αν μείνουμε αυστηρά στην περιοχή της ειδικής σχετικότητας, τότε ναι, δεν υπάρχει τρόπος να πούμε οτι ο ένας από τους δύο είναι “απολύτως” ακίνητος, ενώ ο άλλος κινείται. Όταν όμως πάμε στη γενική σχετικότητα, εκεί θα δούμε οτι υπάρχει κάτι που είναι απόλυτο στο σύμπαν, και που ορίζει ένα “σύστημα αναφοράς” (αγγλ: “reference frame”) που είναι απόλυτο· πρόκειται για το πεδίο Χιγκς (Higgs field), που “γεμίζει” το χώρο του σύμπαντος, και η αλλαγή στην κινητική κατάσταση μέσα σ’ αυτό προκαλεί αυτό που αισθανόμαστε σαν επιτάχυνση ή επιβράδυνση (“φρενάρισμα”). Πράγματι, είτε βάσει ειδικής είτε βάσει γενικής σχετικότητας, ο Β θα παρατηρεί οτι ο χρόνος του Α ρέει με εξαιρετικά βραδύ ρυθμό. Το τί θα γίνει όμως μετά, όταν ο Β και ο Α έρθουν πάλι κοντά ο ένας στον άλλο, διαφέρει μεταξύ ειδικής και γενικής σχετικότητας. Η γενική σχετικότητα είναι η πιο σωστή θεωρία. Την ειδική μπορούμε να τη δούμε απλώς σαν ένα σκαλοπάτι, ένα προαπαιτούμενο για να καταλάβουμε τη γενική. Η ειδική σχετικότητα είναι σωστή μόνο εκεί όπου δεν υπάρχουν μάζες (υλικά σώματα) για να καμπυλώσουν το χώρο. Επομένως η ειδική είναι μια προσεγγιστική περίπτωση της γενικής, και ισχύει μόνο κάτω από την απλουστευτική υπόθεση της ανυπαρξίας μεγάλων μαζών.
Να εξηγήσουμε και γιατί μιλάμε για “διαστολή του χρόνου”, που είναι ο τίτλος αυτής της υποενότητας. Γιατί όταν ο χρόνος “ρέει πιο αργά”, είναι σαν να “διαστέλλεται”. Αν ο Β, καθώς ταξιδεύει με ταχύτητα v στο διαστημόπλοιό του, είχε ένα ρολόι το οποίο το ύψωνε για να δούμε τους δείκτες-του με το υπερτηλεσκόπιό μας, θα βλέπαμε π.χ. τον δευτερολεπτοδείκτη (ή το αντίστοιχο ψηφίο, αν είναι ψηφιακό το ρολόι) να αλλάζει πάρα-πάρα πολύ αργά από το ένα δευτερόλεπτο στο επόμενο. Επομένως είναι σαν το κάθε δευτερόλεπτο να έχει “διασταλεί”, να έχει γίνει μεγαλύτερο. Σε κάθε κινούμενο σώμα λοιπόν, ο χρόνος τοπικά διαστέλλεται.
Αφού όμως ο χρόνος διαστέλλεται, αφού τα δευτερόλεπτα περνούν πιο αργά, δεν σημαίνει άραγε αυτό οτι ένας άνθρωπος κινούμενος με μεγάλη ταχύτητα ζει περισσότερο; Τουλάχιστον, έτσι όπως τον βλέπει ένας παρατηρητής που δεν κινείται μαζί-του; Δεν γερνάει πιο αργά ο Β του παραδείγματός μας, σε σχέση με τον Α; Βεβαίως, και αυτό είναι η βάση του λεγόμενου “παράδοξου των διδύμων”, που θα συζητήσουμε αμέσως μετά.
Πριν από αυτό όμως, ας δούμε την πειραματική επιβεβαίωση του οτι ο χρόνος πράγματι διαστέλλεται.
Οι κοσμικές ακτίνες είναι σωματίδια με εξαιρετικά μεγάλες ενέργειες, που έρχονται σ’ εμάς από οπουδήποτε από το σύμπαν. Όταν φτάνουν στα εξωτερικά στρώματα της ατμόσφαιρας της Γης, προσκρούουν στα σωματίδια που συναντούν εκεί και διασπώνται. Από τη διάσπασή τους δημιουργούνται σωματίδια που λέγονται “μιόνια” (αγγλ.: muons). Βλ. εικόνα, παρακάτω, όπου η κοσμική ακτίνα είναι η ευθεία με το ιώδες χρώμα, και τα μιόνια είναι οι πορτοκαλί ακτίνες. Όπως θα εξηγηθεί αμέσως, αριστερά έχουμε αυτό που θα έπρεπε να συμβαίνει αν η κλασική φυσική ήταν σωστή, ενώ δεξιά αυτό που όντως συμβαίνει λόγω της σχετικότητας.

Τα μιόνια είναι σωματίδια της ίδιας κατηγορίας με τα ηλεκτρόνια (όλα αυτά ονομάζονται “λεπτόνια”), αλλά, αντίθετα με τα σταθερά ηλεκτρόνια που “ζουν” πρακτικά για πάντα, τα μιόνια έχουν “ημιζωή”, όπως λέγεται, που διαρκεί 2,2 μs (μικροδευτερόλεπτα, δηλ. εκατομμυριοστά του δευτερολέπτου). Αυτό σημαίνει οτι αν έχουμε έναν αριθμό μιονίων, π.χ. 100, τότε μετά από 2,2 μs θα έχουν μείνει περίπου τα μισά, δηλαδή περίπου 50, ενώ τα υπόλοιπα θα έχουν διασπαστεί, το καθένα σε ένα ηλεκτρόνιο και δύο νετρίνα. (Γιαυτό λέγεται “ημιζωή”: επειδή σε τόσο χρόνο “μένουν τα μισά”.) Σε άλλα 2,2 μs θα μείνουν περίπου 25 μιόνια, κ.ο.κ.
Τώρα, συμβαίνει το εξής: παρόλο που τα μιόνια, όταν δημιουργούνται, έχουν τεράστιες ταχύτητες, που φτάνουν το 0,98 c (δηλαδή 98% της ταχύτητας του φωτός), εντούτοις ο χρόνος της ημιζωής-τους (2,2 μs: εκατομμυριοστά του δευτερολέπτου!) δεν αρκεί για να φτάσει ένας σημαντικός αριθμός από αυτά ως την επιφάνεια της Γης, από τα ψηλά στρώματα της ατμόσφαιρας όπου δημιουργούνται· ή τουλάχιστον, δεν θα έπρεπε να είναι αρκετός σύμφωνα με την κλασική φυσική (βλ. παραπάνω εικόνα, αριστερή πλευρά). Και όμως, παρατηρούμε ένα σχετικά μεγάλο αριθμό από μιόνια να φτάνουν ως την επιφάνεια της θάλασσας (εικόνα, δεξιά). Γιατί γίνεται αυτό;
Διότι ισχύει η σχετικότητα, και ο χρόνος για το κινούμενο μιόνιο διαστέλλεται! Οπότε τα μιόνια “ζουν παραπάνω”, και κάποια από αυτά προφταίνουν να φτάσουν ως στην επιφάνεια της θάλασσας. Για το ταχύτατα κινούμενο μιόνιο, ο χρόνος περνάει με την κανονική ροή-του, όπως και για τον παρατηρητή Β του διαστημοπλοίου. Αλλά για μας, που είμαστε ακίνητοι ως προς την επιφάνεια της Γης και τα παρατηρούμε, η ημιζωή των μιονίων κρατάει περισσότερο, διαστέλλεται. Ο χρόνος-τους διαστέλλεται.
Σήμερα δεν χρειάζεται να πάμε στην επιφάνεια της θάλασσας και να μετρήσουμε πόσα μιόνια ανά μονάδα χρόνου φτάνουν εκεί. Μπορούμε να δημιουργήσουμε μιόνια, και οποιαδήποτε άλλα σωματίδια, στο εργαστήριο, να τα θέσουμε σε πάρα πολύ μεγάλες ταχύτητες (κοντά στο c), και να μετρήσουμε τις ημιζωές-τους. Μπορούμε δηλαδή να κάνουμε το παραπάνω πείραμα στο εργαστήριο. Τα παλιότερα χρόνια όμως, στα μέσα του 20ού αιώνα, η εργαστηριακή παραγωγή ταχύτατων σωματιδίων δεν ήταν απλό πράγμα, οπότε η φυσική παραγωγή μιονίων από τις κοσμικές ακτίνες λειτούργησε ως ένας εύκολος τρόπος με τον οποίο επιβεβαιωνόταν η ορθότητα της θεωρίας της σχετικότητας και οι λανθασμένες προβλέψεις της κλασικής φυσικής.
Βλέπουμε λοιπόν οτι αφού ο χρόνος διαστέλλεται ακόμα και για τα στοιχειώδη σωματίδια, πόσω μάλλον θα διαστέλλεται για τους βιολογικούς ιστούς του επιβάτη Β του διαστημοπλοίου, αφού οι βιολογικοί ιστοί αποτελούνται από στοιχειώδη σωματίδια. Φυσικά το ίδιο θα ισχύει και για τις σκέψεις-του, αφού οι σκέψεις δημιουργούνται στους νευρώνες του εγκεφάλου, και όταν οι νευρώνες “εκπυρσοκροτούν” πιο αργά, αντίστοιχα πιο αργά θα ξετυλίγονται και οι σκέψεις. Ο Β όμως δεν το καταλαβαίνει αυτό, γιατί για κείνον τα πάντα συμβαίνουν πιο αργά, δεν έχει τίποτα (εντός του διαστημοπλοίου-του) για να συγκρίνει και να καταλάβει οτι αυτό συμβαίνει πιο γρήγορα, ώστε να συμπεράνει οτι ο χρόνος-του έχει διασταλεί. Και αν χρησιμοποιήσει το υπερτηλεσκόπιό του για να κοιτάξει προς τον Α, θα δει το χρόνο του Α να είναι διεσταλμένος, αφού ο Α κινείται με ταχύτητα v ως προς εκείνον.(*)
Μένει να δώσουμε και μια ποσοτική περιγραφή για το κατά πόσο διαστέλλεται ο χρόνος ανάλογα με την ταχύτητα.
Αν λοιπόν η ταχύτητα είναι v, τότε ένα γεγονός που συμβαίνει σε χρόνο t για τον παρατηρητή Α, θα συμβεί σε χρόνο t΄ για τον Β. Σύμφωνα με την κλασική φυσική, οι δύο χρόνοι είνια ίδιοι: t΄ = t. Σύμφωνα με τη σχετικότητα όμως, ο τύπος για το διεσταλμένο χρόνο t΄ είναι λίγο πιο πολύπλοκος.
|
Α Σ Υ Μ Φ Ω Ν Ι Α Α Π Ο Ψ Ε Ω Ν: Ε Ξ Α Ρ Τ Η Σ Η Χ Ρ Ο Ν Ο Υ Α Π Ο Τ Α Χ Υ Τ Η Τ Α |
|||||||
| Η Κ Λ Α Σ Ι Κ Η Α Π Ο Ψ Η | Η Σ Χ Ε Τ Ι Κ Ι Σ Τ Ι Κ Η Α Π Ο Ψ Η | ||||||
|
|
||||||
Και πάλι, η πολυπλοκότητα του σχετικιστικού τύπου δεν είναι ιδιαίτερα μεγάλη. Περιλαμβάνει μόνο την τετραγωνική ρίζα και την ύψωση στο τετράγωνο, πράξεις σε πλήκτρα που περιέχονται σε κομπιουτεράκια τσέπης.
Πιο σημαντικό είναι να παρατηρήσουμε κάτι βαθύτερο:
Στην κλασική άποψη, “ο χρόνος είναι χρόνος”, μόνος-του, και δεν εξαρτάται από τίποτε απολύτως. Είναι σαν το “συμπαντικό ρολόι” να χτυπά τα δευτερόλεπτά του “αδιάφορο”, χωρίς να “νοιάζεται” για το τί συμβαίνει στον κόσμο. Στην κλασική φυσική, αυτός ο “ανεξάρτητος” χρόνος, λέγεται και απόλυτος χρόνος.
Στη σχετικιστική άποψη όμως, ο χρόνος εξαρτάται από το μήκος, που είναι το x στον τύπο. Με άλλα λόγια, ο χρόνος εξαρτάται από το χώρο! (αφού μήκος = χώρος). Αυτό είναι που κάνει τη σχετικότητα τόσο διαφορετική από την κλασική φυσική: οτι ο χρόνος δεν υπάρχει “από μόνος-του”, αλλά είναι πάντα συνάρτηση του χώρου. Χρόνος και χώρος πάνε μαζί στη σχετικότητα, γιαυτό μιλάμε για μια ενιαία οντότητα: το χωροχρόνο.
Συνεπώς, πιο σωστά το παραπάνω πινακάκι θα έπρεπε να έχει τίτλο: “ΕΞΑΡΤΗΣΗ ΧΡΟΝΟΥ ΑΠΟ ΧΩΡΟ”, καθώς η ταχύτητα είναι απλώς το πηλίκο του χώρου (μήκους) διά το χρόνο (σκεφτείτε τις μονάδες-της: χιλιόμετρα ανά ώρα)· επομένως η ταχύτητα δεν αντιπροσωπεύει κάτι το ανεξάρτητο των χώρου και χρόνου. Αλλά επειδή η παρουσίασή μας αυτών των εννοιών ξεκίνησε με το άθροισμα των ταχυτήτων, γιαυτό καταλήξαμε με τις έννοιες όπως παραπάνω.
Ο σχετικιστικός τύπος του παραπάνω πίνακα λέγεται και “μετασχηματισμός Lorentz για το χρόνο”, από τον Ολλανδό φυσικό Hendrik Lorentz (Χέντρικ Λόρεντζ), που διατύπωσε τον τύπο (“μετασχηματισμό”) αυτόν μεταξύ του 1892 και 1899, δηλαδή πριν από τον Αϊνστάιν, μόνο που δεν κατάλαβε τη σημασία-του, και προσπαθούσε μέσω μετασχηματισμών να εξηγήσει τη συμπεριφορά των σωμάτων εντός του αιθέρα. Το 1905, ο Αϊνστάιν χρησιμοποίησε στη δημοσίευσή του τους μετασχηματισμούς Lorentz, κάνοντας αναφορά σ’ αυτόν, αλλά απορρίπτοντας την ανάγκη για χρήση της έννοιας του αιθέρα.
Σε επόμενη ενότητα θα μάθουμε και για το “μετασχηματισμό Lorentz για το χώρο”, όπου θα δούμε το ίδιο πράγμα: οτι ούτε ο χώρος υπάρχει από μόνος-του, αλλά “πάει πακέτο” με το χρόνο. Γιαυτό και (πάλι θυμίζουμε) μιλάμε για χωροχρόνο.
1.5 Το παράδοξο των διδύμων
Το ακόλουθο “πείραμα σκέψης” έχει απασχολήσει τους φυσικούς από την εποχή που ο Αϊνστάιν πρωτοδιατύπωσε την ειδική θεωρία της σχετικότητας.
Ας φανταστούμε δύο δίδυμα αδέλφια, την Άννα και το Βασίλη. Η Άννα παραμένει στη Γη, ενώ ο Βασίλης μπαίνει στο διαστημόπλοιό του, που φυσικά μπορεί να τρέχει με ταχύτητα κοντά στο c, και φεύγει προς μία διεύθυνση, ταξιδεύοντας “ευθεία” και με σταθερή ταχύτητα. Μετά από μερικά χρόνια σταματάει, γυρίζει πίσω, ταξιδεύει τον ίδιο αριθμό ετών με την ίδια ταχύτητα, και φτάνει στη Γη. Ο Βασίλης είναι τώρα νεότερος απ’ τη δίδυμη αδερφή-του Άννα, γιατί όσο ταξίδευε ο χρόνος ήταν διεσταλμένος γι’ αυτόν, όπως ο χρόνος του μιονίου (§1.4). Η διαφορά ηλικίας μεταξύ Άννας και Βασίλη είναι τόσο πιο μεγάλη όσο πιο μεγάλη ήταν η ταχύτητα του Βασίλη σε σύγκριση με το c, και όσο πιο πολύ διήρκεσε το ταξίδι.
|
Α Σ Υ Μ Φ Ω Ν Ι Α Α Π Ο Ψ Ε Ω Ν: Π Ρ Ο Ο Δ Ο Σ Η Λ Ι Κ Ι Α Σ Δ Ι Δ Υ Μ Ω Ν Α Δ Ε Λ Φ Ω Ν |
|||||
| Η Κ Λ Α Σ Ι Κ Η Α Π Ο Ψ Η | Η Σ Χ Ε Τ Ι Κ Ι Σ Τ Ι Κ Η Α Π Ο Ψ Η | ||||
|
|
||||
Μέχρι εδώ δεν υπάρχει πραγματικά κάποιο παράδοξο, εκτός κι αν μας φανεί παράδοξο το γεγονός οτι δύο αδέρφια που γεννήθηκαν δίδυμα κατέληξαν να έχουν διαφορετικές ηλικίες. Παράξενο ίσως, σύμφωνα με τη μέχρι τώρα εμπειρία-μας, αλλά απόλυτα συμβατό με τα όσα μάθαμε ως το σημείο αυτό περί διαστολής του χρόνου στη θεωρία της σχετικότητας. Αλλού βρίσκεται το παράδοξο.
Σύμφωνα με τη θεωρία της ειδικής σχετικότητας, κανένας παρατηρητής δεν δικαιούται να ισχυριστεί οτι εκείνος είναι ακίνητος κατ’ απόλυτη έννοια, ενώ οι άλλοι κινούνται. Ακίνητος ως προς τι; Ως προς την επιφάνεια της Γης; Μα και η Γη κινείται στο διάστημα, περιφερόμενη γύρω από τον Ήλιο. Και ο Ήλιος περιφέρεται γύρω από το κέντρο του Γαλαξία, συμπαρασύροντας το πλανητικό σύστημα μαζί-του. Και ο Γαλαξίας περιφέρεται γύρω από το κοινό κέντρο μάζας του εαυτού-του και του γαλαξία της Ανδρομέδας, όπως και των άλλων μικρότερων γαλαξιών της τοπικής-μας ομάδας. Αλλά, και χωρίς να λάβουμε υπόψη όλες αυτές τις κινήσεις που δείχνουν πως τίποτε δεν είναι απολύτως ακίνητο στο σύμπαν, στη θεωρία της ειδικής σχετικότητας τίθεται σαν αξίωμα οτι ο κάθε παρατηρητής που δεν υφίσταται επιταχύνσεις και επιβραδύνσεις μπορεί να χρησιμοποιεί το δικό-του σύστημα ως σύστημα αναφοράς, και να πει οτι όλοι οι άλλοι κινούνται ως προς το δικό-του σύστημα.
Έτσι και ο Βασίλης, μπορεί να ισχυριστεί οτι εκείνος είναι ακίνητος στο δικό-του σύστημα, αυτό του διαστημοπλοίου. Είναι η Άννα, μαζί με τη Γη — ισχυρίζεται ο Βασίλης — που έφυγαν προς μια διεύθυνση απομακυνόμενοι απ’ αυτόν, έφτασαν ως μια μέγιστη απόσταση, φρενάρησαν, σταμάτησαν, και γύρισαν προς τα πίσω με την ίδια ταχύτητα, ώσπου τον συνάντησαν και πάλι. Σύμφωνα με το Βασίλη, εκείνος θα έπρεπε να είναι πιο γερασμένος από την Άννα. Όταν συναντιώνται όμως, ο ένας θα πρέπει να είναι νεότερος από τον άλλο· μόνο ο ένας από τους δύο μπορεί να έχει δίκιο. Σε κάθε περίπτωση όμως, παραβιάζεται η αρχή της σχετικότητας που λέει οτι κανένας δεν έχει το προνόμιο να είναι ακίνητος κατ’ απόλυτη έννοια. Αλλά αφού ένας απ’ τους δύο θα γεράσει πιο πολύ απ’ τον άλλον, αυτός θα μπορεί να ισχυριστεί οτι έμεινε ακίνητος. Άρα παραβιάζεται η αρχή της ισοδυναμίας των συστημάτων αναφοράς στην ειδική σχετικότητα! Αυτό είναι το παράδοξο.
Αν ο αναγνώστης, που διάβασε προσεκτκά τα παραπάνω, θεωρήσει οτι η Άννα “προφανώς” δεν φεύγει μακριά από το Βασίλη μαζί με ολόκληρη τη Γη, ενώ ένα διαστημόπλοιο φτιάχτηκε για να ταξιδεύει, θυμίζουμε αυτό που είχε αναφερθεί στην §1.4:
«[...] στο υποτιθέμενο αντεπιχείρημα οτι ο Α είναι στη Γη, ενώ ο Β σε διαστημόπλοιο, που “προφανώς” κινείται, θα μπορούσαμε να τους βάλουμε καί τους δυο σε διαστημόπλοια, τον καθένα σε άλλο διαστημόπλοιο φυσικά, και να βρίσκονται μακριά από όλους τους πλανήτες και όλα τα άστρα — π.χ. στο διαγαλαξιακό χώρο. Οπότε τώρα, ποιος κινείται και ποιος μένει ακίνητος; (Εξ ου και “σχετικότητα”, η σχετικότητα της κίνησης.)»
Για το παράδοξο των διδύμων έχουν γίνει πολλές προσπάθειες να λυθεί εντός της θεωρίας της ειδικής σχετικότητας. Κάθε τέτοια προσπάθεια όμως είναι καταδικασμένη να βγει εκτός της ειδικής θεωρίας, και να κάνει έμμεση χρήση του υποβάθρου της θεωρίας της γενικής σχετικότητας, συνήθως ως εξής:
Ο Βασίλης, λέει η απόπειρα επίλυσης του παραδόξου, κάποια στιγμή θα αισθανθεί τη δύναμη της αδράνειας καθώς το διαστημόπλοιό του θα φρενάρει προκειμένου να σταματήσει. Στη συνέχεια, το διαστημόπλοιο θα επιταχύνει κατευθυνόμενο προς τη Γη, οπότε πάλι ο Βασίλης θα αισθανθεί τη δύναμη της επιτάχυνσης να τον έλκει προς το πίσω μέρος του διαστημοπλοίου. Αυτές οι δυνάμεις της επιβράδυνσης και της επιτάχυνσης, τις οποίες η Άννα πίσω στη Γη φυσικά δεν αισθάνεται, “σπάζουν τη συμμετρία” του συστήματος Αννα – Βασίλης, και μας δείχνουν οτι είναι ο Βασίλης που κινείται, και όχι η Άννα. Άρα εκείνος που κινείται (κατ’ απόλυτη έννοια), είναι εκείνος που θα παραμείνει νεότερος (Βασίλης), δηλαδή θα γεράσει πιο αργά από τον άλλον (Άννα).
Το πρόβλημα όμως με την εξήγηση αυτή είναι οτι τη στιγμή που κάνουμε επίκληση σε δύναμη της αδράνειας (λόγω επιτάχυνσης ή επιβράδυνσης) έχουμε φύγει από το πλαίσιο των παραδοχών της ειδικής σχετικότητας, όπου δεν υπάρχουν μάζες σωμάτων στο χώρο. Η μάζα, και η επίδραση που έχει στο χωροχρόνο, αντιμετωπίζεται κατάλληλα στη γενική θεωρία, όπως θα δούμε. Στην ειδική σχετικότητα, ο χώρος είναι κενός. Ένα σώμα μπορεί να κάνει επιταχυνόμενη ή επιβραδυνόμενη κίνηση (αυτό μπορεί να το χειριστεί η ειδική σχετικότητα), αλλά για να πούμε οτι λόγω αυτού του είδους της κίνησης το σώμα δέχεται τη δύναμη της αδράνειας, πρέπει να βγούμε από το πλαίσιο της ειδικής και να πάμε στη γενική σχετικότητα. Εκεί, θα δούμε οτι εισάγεται και πάλι η έννοια του απολύτως κινούμενου σώματος: είναι το σώμα που κινείται ως προς το σύνολο των μαζών των μακρυνών αστεριών και γαλαξιών του σύμπαντος. Σήμερα (αρχές του 21ου αι.) γνωρίζουμε πλέον οτι ένα σώμα που επιταχύνει/επιβραδύνει δέχεται δύναμη (της αδράνειας) που εξηγείται χάρη στην ύπαρξη του πεδίου Χιγκς. Το πεδίο αυτό είναι απόλυτο, όχι σχετικό. Χωρίς το πεδίο αυτό, ο Βασίλης του παραδείγματός μας δεν θα αισθανόταν καμία δύναμη καθώς επιβράδυνε ή επιτάχυνε, και, από τη δική-του σκοπιά, θα ήταν η Άννα την οποία ο Βασίλης θα έβλεπε να επιβραδύνει, να σταματά, και στη συνέχεια να επιταχύνει ερχόμενη προς αυτόν, μέχρι να αποκτήσει σταθερή ταχύτητα.
Επειδή όμως η πραγματικότητα δεν είναι ειδική-σχετικιστική, αλλά είναι γενική-σχετικιστική, είναι όντως ο Βασίλης που αισθάνεται τη δύναμη της αδράνειας και άρα κινείται στο χώρο, γιαυτό είναι εκείνος που θα παραμείνει νεότερος από τη δίδυμη αδελφή-του. Όπως, άλλωστε, είναι το μιόνιο που “ζει περισσότερο” (κατά μέσο όρο) κατά την κίνησή του προς τη Γη, και δεν διαστέλλεται ο χρόνος στη Γη κατά την κίνησή της προς το μιόνιο. Υπάρχει απόλυτη κίνηση στο σύμπαν, αλλά όχι στην ειδική σχετικότητα.
Θα κλείσουμε την υποενότητα αυτή συζητώντας το λόγο για τον οποίο το παράδοξο των διδύμων προκάλεσε τόσες συζητήσεις, και ακόμη προκαλεί. Αρχικά, από το 1905, είχε προταθεί μόνο η θεωρία της ειδικής σχετικότητας, ενώ η γενική σχετικότητα προτάθηκε από το 1915 και μετά. (Καί οι δύο θεωρίες από τον ίδιο άνθρωπο, τον Αϊνστάιν.) Η πιο σημαντική “επαναστατική” ιδέα που εισήγαγε η ειδική σχετικότητα ήταν οτι δεν υπάρχει ούτε απόλυτος χρόνος (ανύπαρκτο το “συμπαντικό ρολόι”, όπως είδαμε στην §1.4), αλλά ούτε και απόλυτος χώρος, με την έννοια οτι κάθε παρατηρητής που βρίσκεται σε “αδρανειακό σύστημα” (όχι επιταχυνόμενο ή επιβραδυνόμενο) έχει τα ίδια δικαιώματα με οποιονδήποτε άλλον παρατηρητή, άλλου, επίσης αδρανειακού συστήματος (κινούμενου ίσως ως προς το πρώτο) ώστε να θεωρήσει τον εαυτό-του “ακίνητο”, και να υπολογίζει όλες τις κινήσεις των άλλων σωμάτων ως προς το δικό-του “υποτιθέμενα ακίνητο” σύστημα (“αδρανειακό” είναι ο δόκιμος όρος).
Αυτή την “επαναστατική ιδέα” της μη απολυτότητας χώρου και χρόνου (που άλλωστε έδωσε και το όνομα στη θεωρία: σχετικότητα, το αντίθετο της απολυτότητας), οι άνθρωποι δεν θέλησαν να την εγκαταλείψουν ούτε ακόμα κι όταν η γενική θεωρία εισήγαγε και πάλι, “από την πίσω πόρτα”, την απολυτότητα του χώρου και χρόνου (ή: χωροχρόνου). Άλλωστε “σχετικότητα” ονομάστηκε και η γενική θεωρία, άρα πώς θα μπορούσε σ’ αυτή να εγκαταλειφθεί η έννοια της σχετικότητας; Και όμως, στη γενική θεωρία, ο χώρος ορίζεται από το σύνολο των μαζών και ενεργειών των σωμάτων που βρίσκονται σ’ αυτόν, που τον καμπυλώνουν, κλπ, θέματα που θα δούμε στη γενική σχετικότητα. “Κενός” χώρος δεν υπάρχει στη γενική σχετικότητα. Έτσι, πάντα υπάρχει ένα σταθερό σημείο αναφοράς για να πούμε ποιος κινείται και ποιος όχι στο σύμπαν: το σύστημα ορίζεται από τις μάζες και ενέργειες των σωμάτων που αποτελούν το σύμπαν. Αλλά και ο χρόνος ξαναπαίρνει ένα είδος απολυτότητας στη γενική θεωρία. Παρόλο που ο χρόνος όντως διαστέλλεται με την κίνηση (όπως και με τα βαρυτικά πεδία, όπως θα μάθουμε), και δεν υπάρχει “παγκόσμιο ρολόι” που χτυπά τα δευτερόλεπτα απ’ άκρη σ’ άκρη του σύμπαντος, μεταφέροντας ακαριαία την “παγκόσμια ώρα” παντού, εντούτοις ο χρόνος στο σύμπαν δεν είναι εντελώς σχετικός· έχει μια αρχή, στη Μεγάλη Έκρηξη· και έχει ένα είδος “τώρα”, παρόλο που αυτό το “τώρα” το έχει ο κάθε παρατηρητής, είναι δηλαδή ένα “σχετικό τώρα”.(*)
Αγκιστρωμένοι λοιπόν οι σκεπτόμενοι άνθρωποι στην επαναστατική ιδέα “σχετικότητα”, δεν θέλησαν να δεχτούν οτι το παράδοξο των διδύμων είναι όντως παράδοξο εντός της ειδικής θεωρίας, ενώ παύει να είναι παράδοξο εντός της γενικής θεωρίας· όπου όμως, το ίδιο το παράδοξο των διδύμων μας αποδεικνύει οτι δεν υπάρχει συμμετρία μεταξύ των δύο παρατηρητών, δηλαδή δεν υπάρχει ακριβώς η σχετικότητα μεταξύ-τους. (Δεν εννοούμε οτι δεν ισχύει η θεωρία της σχετικότητας, αλλά οτι δεν μπορεί ο κάθε παρατηρητής να ισχυριστεί οτι το σύστημά του είναι “το ίδιο” με το σύστημα κάθε άλλου παρατηρητή· υπάρχει ο κινούμενος, που αποδεικνύεται ως τέτοιος γιατί ο χρόνος-του διαστέλλεται, και υπάρχει κι ο μη κινούμενος, που ο χρόνος-του δεν διαστέλλεται.) Γιαυτό μέχρι σήμερα (2η δεκαετία του 21ου αι.), πολλές προσπάθειες εξήγησης της ασυμμετρίας των διδύμων κάνουν χρήση εννοιών ανύπαρκτων στην ειδική σχετικότητα (υπαρκτών στη γενική), όπως η δύναμη της αδράνειας, ενώ ισχυρίζονται οτι παραμένουν εντός του πλαισίου της ειδικής θεωρίας (ιδού ένα παράδειγμα, στα αγγλικά· πολύ καλή η εξήγηση, αλλά κάνει χρήση αδρανειακών δυνάμεων· τα χωρο-χρονικά διαγράμματα που χρησιμοποιεί θα τα γνωρίσουμε σε επόμενη υποενότητα). Υπάρχουν άλλες προσπάθειες, που δεν κάνουν έκκληση σε δυνάμεις αδράνειας, παραμένοντας εντός του πλαισίου της ειδικής σχετικότητας, αλλά οι συγγραφείς-τους δεν αντιλαμβάνονται οτι ακριβώς τα ίδια επιχειρήματα που παραθέτουν από τη σκοπιά του παρατηρητή Α θα μπορούσαν να τεθούν κι από τη σκοπιά του παρατηρητή Β, χωρίς καμία διαφορά, καθώς στην ειδική θεωρία υπάρχει συμμετρία. (Ιδού ένα τέτοιο παράδειγμα, και πάλι στα αγγλικά, προσαρμογή για το περιοδικό Scientific American μιας ανάλυσης του παραδόξου από τον φυσικό και συγγραφέα εκλαϊκευτικών επιστημονικών βιβλίων, Paul Davies.)
1.6 Το παράδοξο της συστολής του μήκους
Ας επανέλθουμε στον παρατηρητή Β, που κάνει το ταξίδι-του με διαστημόπλοιο και με ταχύτητα πολύ κοντά στο c. Είπαμε, στην §1.4, οτι ο χρόνος του Β διαστέλλεται, και μάλιστα τόσο πιο πολύ όσο πιο κοντά στο c είναι η ταχύτητά του. Και είδαμε οτι η φράση «ο χρόνος του Β διαστέλλεται» σημαίνει αυτό το πράγμα κατά κυριολεξία· δηλαδή ο καρδιακός ρυθμός του Β, ο μεταβολισμός-του, οι σκέψεις-του, όλα επιβραδύνονται κατά ένα ποσοστό που εξαρτάται από το c (είδαμε και τον τύπο που δίνει τη σχέση).
Ας φανταστούμε τώρα, σε ένα ακόμη πείραμα σκέψης, οτι είμαστε εμείς στη θέση του Β. Το διαστημόπλοιό μας πρόκειται να διανύσει την απόσταση μέχρι το κοντινότερο άστρο εκτός του πλανητικού-μας συστήματος, που είναι ο Εγγύτατος στον αστερισμό του Κενταύρου,(*) και απέχει από τη Γη 4,24 έτη φωτός, ή 40.141.879.395.160,33 χιλιόμετρα. (Νά γιατί σε αστρονομικές αποστάσεις προτιμάμε τα έτη φωτός από τα χιλιόμετρα: για να έχουμε να χειριστούμε μικρά και λογικά νούμερα!) Θα ταξιδέψουμε ως εκεί με ταχύτητα v = 0,99999999999998906239c, που θα αποκτήσουμε αμέσως μετά από ένα σχετικά μεγάλο διάστημα συνεχούς και σταθερής επιτάχυνσης με τιμή g, δηλαδή με την επιτάχυνση της βαρύτητας. Αυτή η ταχύτητα, η v που μόλις δώσαμε, δεν είναι τυχαία. Θα μας επιτρέψει να φτάσουμε στον Εγγύτατο σε 10 μόλις δευτερόλεπτα! Δηλαδή, ενώ για τον γνωστό-μας παρατηρητή Α στη Γη το ταξίδι-μας θα διαρκέσει σχεδόν ακριβώς 4,24 έτη (αφού η ταχύτητά μας είναι σχεδόν ίση με το c), για μας, τον Β, που ταξιδεύουμε, ο χρόνος θα διασταλεί· και επειδή η ταχύτητά μας v είναι τόσο κοντά στο c, ο διεσταλμένος χρόνος-μας θα διαρκέσει για μας μόνο 10 δευτερόλεπτα. Βέβαια, επειδή το διάστημα κατά το οποίο επιταχυνόμαστε με επιτάχυνση g είναι αρκετά μεγάλο σε μήκος (περίπου το 1/10 του όλου ταξιδιού, όπως το βλέπει ο Α), άρα μεγάλο και σε χρόνο, θα υποθέσουμε οτι το ταξίδι-μας έχει ήδη αρχίσει αρκετά πιο πριν (και “πίσω” από τη Γη), ώστε όταν φτάσουμε στη Γη κατευθυνόμενοι προς τον Εγγύτατο να έχουμε ήδη αποκτήσει την ταχύτητα v που επιθυμούμε.
Θαυμάσια. Ταξιδεύουμε λοιπόν σε ένα ταξίδι που θα διαρκέσει μόνο 10 δευτερόλεπτα (για μας), από τη Γη ως τον Εγγύτατο. Καθόμαστε στη θέση του πιλοτηρίου του διαστημοπλοίου, το οποίο έχει τζάμι, όπως τα αεροπλάνα (είπαμε, είναι πείραμα σκέψης!), ώστε να βλέπουμε έξω: μπροστά-μας, και στα πλάγια. Θέλουμε να μετρήσουμε το μήκος του ταξιδιού-μας, δηλαδή την απόσταση Γης–Εγγυτάτου, την οποία υποθέτουμε οτι δεν γνωρίζουμε. Ή, κι αν τη γνωρίζουμε από τα βιβλία, θέλουμε να τη μετρήσουμε εν πάση περιπτώσει, αφού μπήκαμε στον κόπο να κάνουμε αυτό το ταξίδι. Για το σκοπό αυτό, τη στιγμή που προσπερνάμε τη Γη, στέλνουμε μια ακτίνα φωτός προς τα μπρος, προς τον Εγγύτατο.
Παρόλο που τρέχουμε με μια τόσο μεγάλη v, η ταχύτητα του φωτός και για μας (όπως και για όλους) είναι σταθερή, ίση με c. (Ας θυμηθούμε “το παράδοξο της ταχύτητας του φωτός”, §1.2.) Άρα το φως θα φτάσει στον Εγγύτατο πολύ πριν από τα 10 δικά-μας δευτερόλεπτα. Σ’ αυτά τα 10 δευτερόλεπτα που διήρκεσε το ταξίδι για μας, η ακτίνα του φωτός πρόλαβε να διανύσει όλη την απόσταση από τη Γη ως τον Εγγύτατο! Αλλά σε 10 δευτερόλεπτα, με την ταχύτητα c, το φως διανύει 2.997.924,58 χιλιόμετρα. Επομένως η απόσταση Γης–Εγγυτάτου, έτσι όπως τη βλέπουμε εμείς, δεν μπορεί να είναι μεγαλύτερη από 2.997.924,58 χιλιόμετρα, αφού εμείς ταξιδεύουμε με ταχύτητα v που είναι ελαφρώς μικρότερη από c. Θα είναι λοιπόν μικρότερη από 3 εκατομμύρια χλμ. Αλλά η απόσταση Γης–Εγγυτάτου, έτσι όπως τη μετράει ο ακίνητος Α από τη Γη, είναι όπως είπαμε 40.141.879.395.160,33 χιλιόμετρα — πολύ-πολύ μεγαλύτερη.
Επομένως, ταξιδεύοντας εμείς με αυτή την εξαιρετικά μεγάλη ταχύτητα v, βλέπουμε τα μήκη κατά τη διεύθυνση της κίνησής μας να συστέλλονται! Ενώ τα βιβλία μας λένε οτι η απόσταση αυτή είναι 40.141.879.395.160,33 χιλιόμετρα, εμείς βρίσκουμε οτι είναι πιο μικρή από 2.997.924,58 χιλιόμετρα. Η διαστολή του χρόνου λοιπόν συνοδεύεται από συστολή του μήκους!
Και πόσο συστέλλονται τα μήκη, σε συνάρτηση με την ταχύτητα v; Ορίστε ο τύπος της συστολής του μήκους, που μοιάζει λίγο με τον τύπο για τη διαστολή του χρόνου (έχουν και οι δύο τον ίδιο παρονομαστή, αλλά ο αριθμητής εδώ είναι απλούστερος):
|
Α Σ Υ Μ Φ Ω Ν Ι Α Α Π Ο Ψ Ε Ω Ν: Ε Ξ Α Ρ Τ Η Σ Η Μ Η Κ Ο Υ Σ Α Π Ο Τ Α Χ Υ Τ Η Τ Α |
|||||||||
| Η Κ Λ Α Σ Ι Κ Η Α Π Ο Ψ Η | Η Σ Χ Ε Τ Ι Κ Ι Σ Τ Ι Κ Η Α Π Ο Ψ Η | ||||||||
|
|
||||||||
Όταν λέμε “αληθινό” μήκος και “αληθινό” χρόνο στο σχετικιστικό πλαίσιο, εννοούμε το μήκος και το χρόνο που μετράει ο άλλος παρατηρητής, ο Α.
Ο σχετικιστικός τύπος του παραπάνω πίνακα λέγεται και “μετασχηματισμός Lorentz για το μήκος”.
Βάζοντας τις τιμές που γνωρίζουμε για τα x, v, και t στον παραπάνω σχετικιστικό τύπο, δηλαδή όπου x = 40.141.879.395.160,33 χλμ, όπου v = 0,99999999999998906239c, και όπου t = 133.898.896,8 δευτερόλεπτα (γιατί τόσα δευτερόλεπτα είναι τα 4,234 χρόνια, που είναι η πιο ακριβής απόσταση του Εγγυτάτου), βρίσκουμε x΄ = 2.938.797,58 χιλιόμετρα. Όπως βλέπουμε, αυτός ο αριθμός είναι λίγο μικρότερος από τα 2.997.924,58 χιλιόμετρα που προλαβαίνει να διανύσει το φως σε 10 δευτερόλεπτα. Αυτό, το x΄, θα είναι το μήκος της απόστασης Γης–Εγγυτάτου που θα μετρήσουμε ως κινούμενοι παρατηρητές. Το μήκος θα έχει υποστεί τεράστια συστολή!
Στο σημείο αυτό είναι ενδιαφέρον να σκεφτούμε τί σημαίνουν τα παραπάνω. Ας υποθέσουμε οτι μπορούμε να πραγματοποιήσουμε το παραπάνω ταξίδι των 10 δευτερολέπτων. Τί θα βλέπαμε τότε; Θα βλέπαμε τα μήκη, κατευθείαν εμπρός-μας, να είναι “συμπιεσμένα”;
Το τί θα βλέπαμε, έχει να κάνει με τον τρόπο που λειτουργεί η διοπτική όραση στον άνθρωπο. Για να αντιληφθούμε σε πόσο βάθος βρίσκονται τα αντικείμενα, κοντά-μας ή μακριά-μας, έχουμε πολλούς μηχανισμούς, ο πιο σημαντικός από τους οποίους είναι η διοπτική όραση· δηλαδή το οτι έχουμε δύο μάτια, και κάθε μάτι μας δείχνει τον κόσμο από ελαφρά διαφορετική “οπτική γωνία”. Από τις διαφορές των δύο εικόνων, αριστεράς και δεξιάς, αντιλαμβανόμαστε το βάθος (βλ. σχήμα).
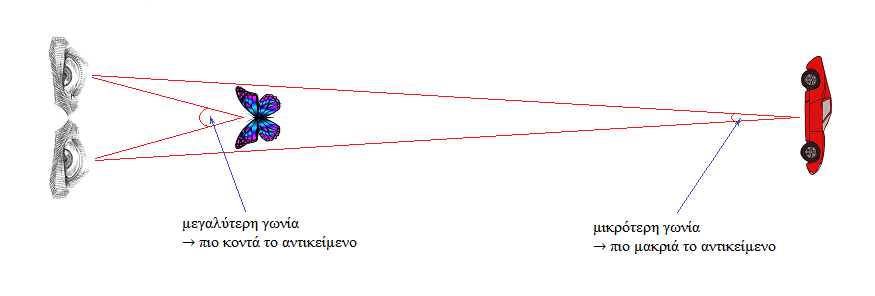
Έχουμε κι άλλους τρόπους να αντιλαμβανόμαστε το βάθος, όπως η σκίαση των αντικειμένων, η πιθανή αλληλοκάλυψή τους, το φαινόμενο μέγεθός τους όταν πρόκειται για γνωστού μεγέθους αντικείμενα (π.χ., ένα αυτοκίνητο: “μικρό” σε απόσταση, “μεγάλο” κοντά-μας), ο κορεσμός των χρωμάτων (π.χ.: ένα βουνό φαίνεται ξέθωρο και γαλαζωπό σε απόσταση, αλλά πιο καθαρό και με πιο “ζωντανά”–κορεσμένα χρώματα όταν είναι πιο κοντά), και πιθανώς και άλλους. Δυστυχώς, όλοι αυτοί οι μηχανισμοί καθίστανται ανίσχυροι όταν βλέπουμε προς το διάστημα. Η διοπτική όραση λειτουργεί μόνο για αντικείμενα έως μερικές δεκάδες μέτρα μακριά-μας. Στο διάστημα δεν υπάρχει ούτε σκίαση, ούτε αλληλοκάλυψη αντικειμένων, ούτε κορεσμός χρωμάτων, κλπ. Αποτυγχάνουμε λοιπόν εντελώς να δούμε το βάθος. Αυτός είναι και ο λόγος που όλα τα αστέρια μας φαίνονται “καρφωμένα” σε έναν υποτιθέμενο “ουράνιο θόλο”, ενώ οι πραγματικές-τους αποστάσεις διαφέρουν εξαιρετικά μεταξύ-τους. (Π.χ.: ο Σείριος είναι 8,6 έτη φωτός μακριά, αλλά ο Ντενέμπ απέχει ~2600 έτη φωτός.) Άρα το συσταλμένο μήκος δεν θα μπορούσαμε να το αντιληφθούμε κατευθείαν, με τα μάτια-μας. Μέσω μετρήσεων όμως, ναι, θα βρίσκαμε οτι τα μήκη κατευθείαν εμπρός-μας έχουν υποστεί συστολή. Παραμένει όμως το ερώτημα: ποια θα ήταν η εξέλιξη του ταξιδιού καθώς θα βλέπαμε τα αστέρια μπροστά-μας;
Αν ταξιδεύαμε προς ένα πλανητικό σύστημα άλλου αστέρα, και το ταξίδι διαρκούσε για μας π.χ. ένα λεπτό της ώρας, ενώ για τον παρατηρητή της Γης διαρκούσε 600 χρόνια, και ο αστέρας είχε έναν πλανήτη που περιφέρεται γύρω-του π.χ. μια φορά κάθε έτος, και μπορούσαμε να παρατηρήσουμε τον πλανήτη με το υπερτηλεσκόπιό μας, θα βλέπαμε μέσα στο ένα λεπτό που θα διαρκούσε το ταξίδι όλες τις 600 περιφορές του πλανήτη γύρω από τον αστέρα. Επομένως ο πλανήτης θα φαινόταν να στροβιλίζεται με την ταχύτητα που στροβιλίζεται περίπου το τύμπανο ενός πλυντηρίου όταν στίβει τα ρούχα. Θα βλέπαμε δηλαδή το σύμπαν σε γρήγορη κίνηση, προς την “κατευθείαν εμπρός” διεύθυνση. Επίσης τα χρώματα των αστεριών, κατευθείαν εμπρός, θα ήσαν ελαφρώς μετατοπισμένα προς το μπλε (στο φάσμα, λέμε «προς το ιώδες»).(*) Αντίστοιχα, αν κοιτούσαμε προς τα πίσω, ο κόσμος θα έτρεχε σε αργή κίνηση, και τα αστέρια θα είχαν μετατοπισμένο το χρώμα-τους προς το ερυθρό. Προς τη διεύθυνση που είναι κάθετη στην κίνησή μας, δεν θα παρατηρούσαμε καμία διαφορά. Όταν σταματούσαμε, η κίνηση και τα χρώματα θα επανέρχονταν στο “φυσιολογικό”. Όμως τον παρατηρητή Α στη Γη θα τον βλέπαμε να έχει γεράσει πολύ λίγο, πιο λίγο κι από το δικό-μας ένα λεπτό της πτήσης. Αν αντιστρέφαμε την πορεία και επιστρέφαμε στη Γη με την ίδια ταχύτητα, θα βλέπαμε εντός του ενός λεπτού να περνούν τα 600 χρόνια που κάναμε σύμφωνα με τους γήινους παρατηρητές για να φτάσουμε στο άστρο, συν άλλα 600 χρόνια που κάναμε (πάντα σύμφωνα με τους γήινους) για να γυρίσουμε. Επομένως 1200 χρόνια θα περνούσαν εντός ενός λεπτού μπροστά στα μάτια-μας, σε “γρήγορη κίνηση”.
Ας σημειώσουμε οτι και ο παρατηρητής Α θα βλέπει τον ταξιδιώτη Β και το διαστημόπλοιό του “συμπιεσμένους”, εφόσον μπορεί να παρακολουθεί τον ταχύτατα κινούμενο Β με το υπερτηλεσκόπιό του.
Σ Υ Ν Ε Χ Ι Ζ Ε Τ Α Ι . . .
2. Στοιχεία Γενικής Σχετικότητας
2.0 Προαπαιτούμενα
Για να μπορέσουμε να κατανοήσουμε τις έννοιες της θεωρίας της γενικής σχετικότητας, θα ξεκινήσουμε από κάποιες έννοιες που είναι στοιχειώδεις (τόσο στην κλασική φυσική όσο και στη σχετικότητα), και θα τις γενικεύσουμε, ώστε να καταλάβουμε οτι οι λέξεις των εννοιών αυτών έχουν διαφορετική σημασία στη φυσική απ’ ότι στην καθομιλουμένη γλώσσα. Έτσι, η παρούσα ενότητα, τα “προαπαιτούμενα”, δεν ασχολείται καθαυτό με τη σχετικότητα, αλλά χτίζει τη βάση πάνω στην οποία θα στηριχτεί η θεωρία της γενικής σχετικότητας, που θα παρουσιαστεί κατόπιν.
2.0.1 Η έννοια της διάστασης και του χώρου
Η πρώτη έννοια που θα διαφοροποιήσουμε εδώ από την καθομιλουμένη γλώσσα είναι η έννοια της “διάστασης”. Η λέξη “διάσταση” στην καθομιλουμένη σημαίνει πολλά και διάφορα πράγματα. Π.χ. μπορεί να σημαίνει τη “διαφορά”, όπως όταν λέμε: «παρουσίασαν διάσταση απόψεων»· δηλαδή «διαφώνησαν». Ή μπορεί να σημαίνει την “επιπλέον ιδιότητα”, όπως όταν λέμε: «θα μιλήσω για μια άλλη διάσταση του θέματος». Αυτές οι χρήσεις της λέξης “διάσταση” δεν έχουν παρά την πιο αμυδρή και ελαχιστότατη σχέση με την έννοια της διάστασης όπως χρησιμοποιείται στη φυσική και στα μαθηματικά, και καλό είναι να ξεχάσουμε τις έννοιες της λέξης αυτής στην καθομιλουμένη, αν θέλουμε να καταλάβουμε τη φυσικο–μαθηματική έννοια της λέξης “διάσταση”.
Αντίστοιχο επανακαθορισμό και γενίκευση θα κάνουμε στην έννοια “χώρος”.
2.0.1.1 Οι πιο απλές και στοιχειώδεις διαστάσεις
Οι πιο απλές διαστάσεις στη φυσική και στα μαθηματικά είναι αυτές που υλοποιούνται από κάθε γωνιά ενός τυπικού ορθογώνιου δωματίου, όπως αυτή που φαίνεται στο ακόλουθο διάγραμμα:
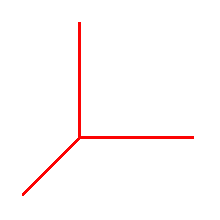
Κάθε δωμάτιο έχει συνήθως οκτώ τέτοιες γωνίες: τέσσερις στο πάτωμα, και τέσσερις στο ταβάνι. Οι διαστάσεις, στο παραπάνω διάγραμμα, είναι οι τρεις κόκκινες ευθείες που συναντώνται στη γωνία. Ολόκληρο το πλαίσιο με τις τρεις ευθείες λέγεται σύστημα συντεταγμένων (θα δούμε σε λίγο γιατί). Το σημείο του πλαισίου (στη γωνία) όπου συναντώνται οι τρεις διαστάσεις λέγεται αρχή του συστήματος συντεταγμένων.
Τώρα, το παραπάνω διάγραμμα είναι παραπλανητικό, γιατί οι διαστάσεις δεν σταματούν στην αρχή του συστήματος συντεταγμένων, ούτε αρχίζουν από εκεί, αλλά συνεχίζονται και προς την άλλη κατεύθυνση, όπως δείχνει το επόμενο διάγραμμα. (Οι “συνέχειες” αυτές φαίνονται με ροζ χρώμα.)
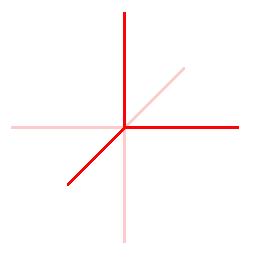
Θα μπορούσαμε να φανταστούμε το δωμάτιο με διάφανους τοίχους, και να έχει άλλα δωμάτια κολλητά σ’ αυτό, προς τα αριστερά, προς τα κάτω, και προς τα πίσω, αν αυτό βοηθάει. Ακόμα καλύτερα, θα μπορούσαμε να φανταστούμε οτι δεν υπάρχουν τοίχοι, αλλά οι ευθείες στο παραπάνω διάγραμμα είναι τρία σύρματα, που τέμνουν κατά ορθή γωνία (90°) το ένα το άλλο. Ας πάρουμε τώρα ένα από αυτά τα “σύρματα”, δηλαδή μία διάσταση, και ας “ζουμάρουμε” για να δούμε από τί αποτελείται:
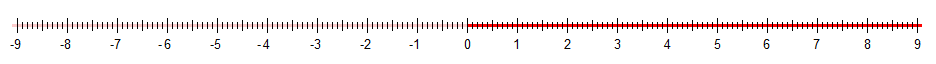
Βλέπουμε οτι πάνω στη διάσταση έχουν σημειωθεί ορισμένες διαβαθμίσεις, ώστε η διάσταση θυμίζει χάρακα. Η αρχή της διάστασης αυτής έχει σημειωθεί με το 0 (μηδέν). Δεξιά της αρχής, οι διαβαθμίσεις λέγονται θετικές συντεταγμένες, ενώ αριστερά της αρχής λέγονται αρνητικές συντεταγμένες. (Νά γιατί το πλαίσιο των τριών διαστάσεων, σε προηγούμενο διάγραμμα, ονομάζεται “σύστημα συντεταγμένων”.) Η διάσταση συνεχίζει, τόσο προς τα δεξιά (θετικές συντεταγμένες) όσο και προς τ’ αριστερά (αρνητικές), χωρίς όριο, μέχρι το άπειρο.
Η ευθεία γραμμή πάνω στην οποία τοποθετήσαμε τη διάσταση με τις διαβαθμίσεις-της ονομάζεται χώρος μίας διάστασης. Κάθε σημείο του χώρου, δηλ. πάνω στην ευθεία της διάστασης (και όχι μόνο στις διαβαθμίσεις) αντιστοιχεί σε έναν αριθμό. Π.χ., μεταξύ του 1 και του 2 είναι το 1.5 (θα χρησιμοποιούμε την τελεία για υποδιαστολή, γιατί το κόμμα σε λίγο θα το χρησιμοποιήσουμε για άλλο σκοπό). Η επόμενη διαβάθμιση είναι το 1.6· αλλά και μεταξύ του 1.5 και του 1.6 υπάρχει το 1.55· κ.ο.κ., με κάθε αριθμό (με οσαδήποτε δεκαδικά ψηφία) να αντιπροσωπεύεται από ένα σημείο πάνω στη διάσταση. Έτσι, κάθε σημείο του χώρου έχει αποκτήσει ένα “όνομα”, μια “ετικέττα”, που είναι ο αντίστοιχος αριθμός-του.
|
Σε ένα χώρο μίας διάστασης,
κάθε σημείο χαρακτηρίζεται από έναν αριθμό. |
Ας πάρουμε τώρα δύο από τις τρεις διαστάσεις του πλαισίου που συναντήσαμε προηγουμένως, και ας τις τοποθετήσουμε πάνω στην επιφάνεια της παρούσας σελίδας:
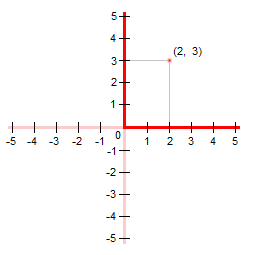
Έτσι η επιφάνεια (το επίπεδο) της παρούσας σελίδας αποκτά δύο διαστάσεις και ονομάζεται χώρος δύο διαστάσεων. Κάθε σημείο της επιφάνειας (του χώρου αυτού) αποκτά ένα όνομα, που είναι οι δύο αριθμοί που του αντιστοιχούν σε κάθε διάσταση. Για παράδειγμα, στο παραπάνω διάγραμμα σημειώνεται το σημείο (2, 3), καθώς αν από αυτό το σημείο φέρουμε μια κάθετο, αυτή θα τμήσει την οριζόντια διάσταση στο σημείο 2, ενώ αν από το ίδιο σημείο φέρουμε μια οριζόντια, αυτή θα τμήσει την κατακόρυφη διάσταση στο σημείο 3. Έτσι, έχουμε τον κανόνα:
|
Σε ένα χώρο δύο διαστάσεων,
κάθε σημείο χαρακτηρίζεται από δύο αριθμούς. |
Ο πρώτος αριθμός κάθε σημείου λέγεται η x-συντεταγμένη του σημείου, και ο δεύτερος αριθμός λέγεται η y-συντεταγμένη. Έτσι, γενικά κάθε σημείο ενός χώρου δύο διαστάσεων το συμβολίζουμε με (x, y). Την οριζόντια διάσταση, που έχει τις x-συντεταγμένες, την ονομάζουμε και άξονα X, ενώ την κατακόρυφη διάσταση με τις y-συντεταγμένες την ονομάζουμε και άξονα Y. (Τα δύο αυτά γράμματα μπορούμε να τα διαβάσουμε και στα ελληνικά σαν Χι–Ψι.)
Η μεταφορά των παραπάνω εννοιών σε τρεις διαστάσεις δεν παρουσιάζει καμμία δυσκολία: βάζουμε συντεταγμένες σε κάθε μία από τις τρεις διαστάσεις του πλαισίου που είδαμε στο δεύτερο διάγραμμα της σελίδας, και δίνουμε έτσι όνομα σε κάθε σημείο του χώρου τριών διαστάσεων, γράφοντας τρεις αριθμούς σε παρένθεση: (x, y, z). Κατά σύμβαση, τον τρίτο αριθμό τον λέμε z-συντεταγμένη, και την αντίστοιχη διάσταση άξονα Ζ (Ζήτα, αν το διαβάσουμε στα ελληνικά).
|
Σε ένα χώρο τριών
διαστάσεων, κάθε σημείο χαρακτηρίζεται από τρεις αριθμούς. |
Κατά σύμβαση επίσης, προκειμένου για χώρο τριών διαστάσεων, τον άξονα Ζ συνήθως τον αντιστοιχούμε στην κατακόρυφη ευθεία (βλ. διάγραμμα παρακάτω), ενώ τον άξονα Y στην ευθεία που εμφανίζεται πλάγια. Ο άξονας Χ είναι βέβαια η οριζόντια ευθεία.
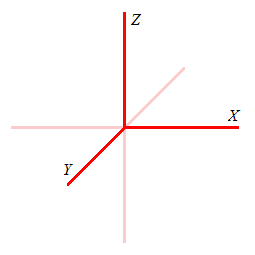
Συνοψίζοντας:
Μια ευθεία γραμμή, που είναι χώρος μιας διάστασης, λέγεται και μονοδιάστατος χώρος.
Ένα επίπεδο, όπως αυτή η σελίδα, που είναι χώρος δύο διαστάσεων, λέγεται και διδιάστατος χώρος.
Ο χώρος στον οποίο ζούμε και κινούμαστε, που είναι χώρος τριών διαστάσεων, λέγεται και τριδιάστατος χώρος.(*)
Όλα τα παραπάνω είναι βέβαια γνωστά από τα μαθηματικά του γυμνασίου–λυκείου. Τώρα θα κάνουμε ένα βήμα πέρα από τη γνώση αυτή.
2.0.1.2 Τέσσερις διαστάσεις: όπου η εποπτική αντίληψη αρχίζει να χωλαίνει
Ας υποθέσουμε οτι τα σημεία του τριδιάστατου χώρου δεν υπάρχουν στις θέσεις-τους αιώνια, αλλά εμφανίζονται για μια μόνο στιγμή και μετά εξαφανίζονται. Για παράδειγμα, το σημείο (8, 2.5, -3.6) “ανάβει” ξαφνικά τη χρονική στιγμή 1.3 δευτερόλεπτα (από τότε που ξεκινήσαμε το χρονόμετρό μας), και αμέσως (την ίδια στιγμή) “σβήνει”. Αυτό τότε δεν θα το λέμε σημείο, αλλά γεγονός, και θα του προσθέσουμε τη χρονική συντεταγμένη 1.3, ώστε το γεγονός αυτό να έχει τέσσερις συντεταγμένες: (8, 2.5, -3.6, 1.3).
Μπορεί μάλιστα το ίδιο σημείο (8, 2.5, -3.6) να “αναβοσβήσει” και τη χρονική στιγμή 5.2, οπότε το (8, 2.5, -3.6, 5.2) θα αποτελέσει ένα άλλο γεγονός, που απλώς “συνέβη” στο ίδιο σημείο του τριδιάστατου χώρου, αλλά μια διαφορετική στιγμή. Έτσι μπορούμε να έχουμε δύο ή και περισσότερα γεγονότα στο ίδιο σημείο, που να διαφέρουν μόνο κατά το χρόνο κατά τον οποίο συνέβησαν.
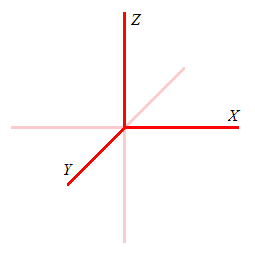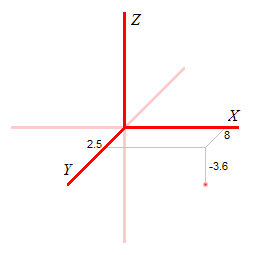
Παράδειγμα γεωμετρικής παράστασης διαφορετικών γεγονότων,
που συμβαίνουν στο σημείο (8, 2.5, -3.6) κάθε 1.3 δευτερόλεπτα.
Με τον τρόπο αυτό έχουμε προσθέσει μια τέταρτη διάσταση, το χρόνο, στον προηγούμενο τριδιάστατο χώρο, κατασκευάζοντας έτσι ένα χώρο τεσσάρων διαστάσεων, ή πιο σύντομα, έναν τετραδιάστατο χώρο. Τις τέσσερις συντεταγμένες των γεγονότων του τετραδιάστατου χώρου τις συμβολίζουμε έτσι: (x, y, z, t)· και την τέταρτη διάσταση τη λέμε άξονα Τ (από το αγγλικό time = χρόνος).
Βέβαια, για τον τετραδιάστατο αυτό χώρο δεν έχουμε εύκολη εποπτική αντίληψη. Η ανθρώπινη ικανότητα γεωμετρικής αντίληψης σταματάει στις τρεις διαστάσεις. Ενώ δηλαδή μπορούμε να φανταστούμε για όσο χρόνο θέλουμε (και φυσικά να δούμε με τα μάτια-μας) μια σφαίρα τριών διαστάσεων (π.χ. μια μπάλα ποδοσφαίρου, αλλά περιλαμβανομένου και του εσωτερικού-της), αντίθετα, για να δούμε μια σφαίρα τεσσάρων διαστάσεων θα πρέπει να την κάνουμε να εμφανίζεται σε εικόνα αυτής της ιστοσελίδας σταδιακά, ξεκινώντας από ένα μικρό σημείο, μεγαλώνοντας και φτάνοντας σε μια μέγιστη διάμετρο, και μετά μικραίνοντας και φτάνοντας πάλι σε σημείο, ώσπου να εξαφανιστεί εντελώς. Μάλιστα και ο τρόπος που η σφαίρα, ή μάλλον οι διαδοχικές σφαίρες, θα μεγαλώνουν και θα μικραίνουν πρέπει να είναι συγκεκριμένος, ώστε να πούμε οτι αυτό που βλέπουμε αποτελεί τετραδιάστατη σφαίρα, και όχι ελλειψοειδές (αβγό), ή κάτι άλλο. Μπορούμε επίσης να γράψουμε την αλγεβρική εξίσωση της τετραδιάστατης σφαίρας, γενικεύοντας με έναν απλούστατο τρόπο την αλγεβρική εξίσωση της τριδιάστατης σφαίρας, αλλά γεωμετρικά δεν έχουμε έναν απλό τρόπο ώστε να φανταστούμε ένα τέτοιο αντικείμενο, τουλάχιστον τόσο απλό όσο έχουμε για τα τριδιάστατα αντικείμενα. Πρόκειται για περιορισμό που τίθεται από την ανθρώπινη νοημοσύνη, από το “εργοστάσιο κατασκευής-μας” (που δεν είναι άλλο από τη βιολογική εξέλιξη). Και μάλιστα, η εξήγηση του ανθρώπινου αυτού περιορισμού, δηλαδή το “γιατί αντιλαμβανόμαστε μόνο μέχρι τρεις διαστάσεις, και όχι περισσότερες”, γίνεται κατανοητή μόνο μέσω της θεωρίας της σχετικότητας, όπως θα μάθουμε προς το τέλος του παρόντος μαθήματος.
Ευτυχώς όμως, για να προχωρήσουμε, δεν θα χρειαστεί να φανταζόμαστε τετραδιάστατα αντικείμενα. Άλλωστε, όπως θα δούμε αργότερα, η απλή προσθήκη μιας ακόμα διάστασης, όπως ο άξονας Τ, δεν μας οδηγεί ακριβώς στη θεωρία της σχετικότητας, αλλά στη λεγόμενη “Γαλιλαιική γεωμετρία” (ή “γεωμετρία του Γαλιλαίου”), που δεν είναι παρά η Ευκλείδεια στερεομετρία (γεωμετρία των στερεών σωμάτων, της οποίας κάποια στοιχεία μαθαίνουμε στο λύκειο), με την προσθήκη μιας ακόμα διάστασης. Για τη θεωρία της σχετικότητας θα χρειαστεί να κάνουμε κάτι στον τρόπο που μετράμε τα μήκη πάνω στην τέταρτη διάσταση, το οποίο διαφέρει από τον οικείο τρόπο μέτρησης μηκών στη Γαλιλαιική / Ευκλείδεια γεωμετρία. Αυτά όμως θα τα δούμε σε λίγο.
2.0.1.3 Γενίκευση σε μη γεωμετρικές διαστάσεις
Η γενίκευση που θα κάνουμε τώρα δεν είναι απαραίτητη για τη θεωρία της σχετικότητας, θα μας δώσει όμως μια πιο ολοκληρωμένη γνώση για τις έννοιες “διάσταση” και “χώρος”. Άλλωστε συναντούμε γενικεύσεις των εννοιών αυτών σε άλλους τομείς της φυσικής, όπως η κβαντική φυσική (όπου, σε κάποιες θεωρίες, μιλάμε για “χώρο 11 διαστάσεων”)· οπότε καλό είναι να δούμε το θέμα και στην πλήρη γενικότητά του. Θα συνδέσουμε, επίσης, τα όσα θα δούμε, με θέματα της θεωρίας της σχετικότητας.
Ας θεωρήσουμε την οθόνη του υπολογιστή στην οποία διαβάζουμε το παρόν κείμενο. Η οθόνη αυτή αποτελείται από εικονοστοιχεία, ή pixels για συντομία. (Πλησιάζοντας το μάτι στην οθόνη μπορούμε να δούμε τα pixels ένα-προς-ένα.) Βέβαια το κάθε pixel έχει κάποιο μέγεθος, δεν είναι χωρίς καθόλου μέγεθος όπως θεωρούμε οτι είναι τα σημεία. Αλλά θα υποθέσουμε εδώ, χάριν ευκολίας, οτι το κάθε pixel κατέχει μια θέση ενός σημείου στο χώρο, και επειδή η επιφάνεια της οθόνης είναι ένας διδιάστατος χώρος, αρκούν δύο συντεταγμένες για να περιγράψουν τη θέση του κάθε pixel στην οθόνη — όπως άλλωστε γνωρίζει πολύ καλά όποιος έχει προγραμματίσει “γραφικά” σε υπολογιστές. Έτσι, π.χ. το (200, 100) είναι ένα pixel που βρίσκεται 200 θέσεις από το αριστερό άκρο της οθόνης (ή του “παραθύρου” — δεν έχει σημασία), και 100 θέσεις από το άνω(*) άκρο της οθόνης (ή παραθύρου).
Ένα pixel όμως δεν χαρακτηρίζεται απλώς από μια θέση στην οθόνη· έχει και ένα χρώμα. Το χρώμα ενός pixel μπορεί να οριστεί με διάφορους τρόπους, δύο από τους οποίους βλέπουμε στο διάγραμμα παρακάτω, που είναι ένα “παράθυρο διαλόγου” για τον καθορισμό χρώματος, πολύ γνωστό σε χρήστες του λειτουργικού συστήματος Windows:
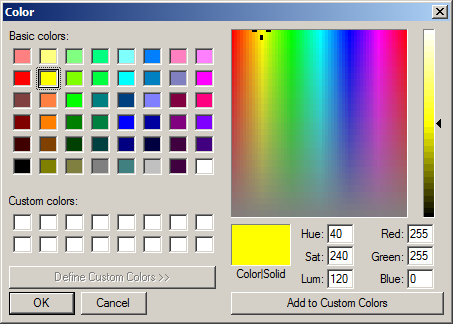
Στο παραπάνω παράθυρο διαλόγου βλέπουμε πώς καθορίζεται το καθαρό κίτρινο (“καναρινί”). Στην κάτω-δεξιά γωνία του διαλόγου βλέπουμε τις τιμές 255, 255, 0, που αντιστοιχούν στις “ποσότητες” κόκκινου (Red), πράσινου (Green), και μπλε (Blue), που έχει το χρώμα αυτό· δηλαδή το “καναρινί” έχει τις μέγιστες ποσότητες κόκκινου και πράσινου (255 — αυτή είναι η μέγιστη τιμή), και την ελάχιστη ποσότητα μπλε, δηλαδή 0 — καθόλου. Οι τρεις αυτές τιμές, (255, 255, 0), μπορούμε να πούμε οτι είναι οι συντεταγμένες του χρώματος αυτού σε έναν αφηρημένο “χώρο χρωμάτων”, τριών διαστάσεων, όπου η κάθε διάσταση δηλώνει την ποσότητα κόκκινου, πράσινου, και μπλε που έχει κάθε χρώμα, και παίρνει τιμές από 0 έως 255. Το κάθε χρώμα είναι ένα σημείο στο χώρο αυτόν, με τρεις συντεταγμένες. Π.χ. το καθαρό κόκκινο (της “πυροσβεστικής” — το βλέπουμε στη 2η σειρά, 1η στήλη, στον πίνακα των προκαθορισμένων χρωμάτων του διαλόγου) έχει συντεταγμένες (255, 0, 0)· το καθαρό πράσινο (3η σειρά, 3η στήλη) έχει συντεταγμένες (0, 255, 0)· και το καθαρό μπλε (4η σειρά, 5η στήλη) έχει συντεταγμένες (0, 0, 255). Ο ίδιος διάλογος μας δίνει και ένα δεύτερο σύστημα συντεταγμένων για τον ίδιο χώρο χρωμάτων, που βασίζεται σε τρία άλλα χαρακτηριστικά του κάθε χρώματος: την απόχρωση (ποιότητα) του χρώματος (“hue”), τον κορεσμό σε χρώμα (“saturation”) και τη φωτεινότητα (“luminosity”), όπου το κίτρινο βλέπουμε οτι έχει συντεταγμένες (40, 240, 120) στις διαστάσεις αυτές. Δεν θα επιμείνουμε όμως σ’ αυτό το άλλο σύστημα συντεταγμένων, γιατί η κατανόηση του πρώτου μας αρκεί. Απλά σημειώνουμε εδώ την εξής πολύ χρήσιμη παρατήρηση:
|
Ένας χώρος μπορεί να έχει
περισσότερα του ενός συστήματα συντεταγμένων. |
Στη θεωρία της σχετικότητας θα μιλήσουμε περί “αλλαγής του συστήματος συντεταγμένων”, επομένως ας προσέξουμε την παραπάνω παρατήρηση:
Στο σύστημα συντεταγμένων που έχει άξονες τα “κόκκινο, πράσινο, μπλε”, το “κίτρινο-καναρινί” έχει συντεταγμένες: (255, 255, 0).
Ενώ στο σύστημα συντεταγμένων με άξονες τα “απόχρωση, κορεσμός, φωτεινότητα”, το ίδιο χρωμα έχει συντεταγμένες: (40, 240, 120).
Όπως ήδη παρατηρήσαμε λοιπόν, ένα pixel της οθόνης έχει τόσο μια θέση (x, y) στην οθόνη όσο και ένα χρώμα (r, g, b), όπου r = red, g = green, και b = blue. Επομένως το pixel βρίσκεται σε έναν πενταδιάστατο χώρο, οι πλήρεις συντεταγμένες του οποίου γράφονται έτσι: (x, y, r, g, b). (Δεν έχει σημασία η σειρά με την οποία γράφουμε τις διαστάσεις· αυθαίρετα αποφασίσαμε τη σειρά αυτή· άπαξ και αποφασίσουμε όμως τη σειρά, πρέπει να τη διατηρούμε πάντοτε ίδια.)
Αν είχαμε δυσκολία να παραστήσουμε γεωμετρικά τον τετραδιάστατο χώρο των 3+1 διαστάσεων (τριών χωρικών και μιας χρονικής) νωρίτερα, τώρα είμαστε εντελώς ανήμποροι να παραστήσουμε γεωμετρικά τον πενταδιάστατο χώρο των pixels.
Άλλη χρήσιμη παρατήρηση είναι οτι ούτε η θέση ενός pixel, ούτε το χρώμα-του είναι αριθμοί που γίνονται οσοδήποτε μεγάλοι, όπως συνέβαινε στα πρώτα παραδείγματα που είδαμε στο παρόν κείμενο. Εδώ, οι θέσεις των pixels περιορίζονται από το πόσο μεγάλη είναι η “ανάλυση” της οθόνης, ενώ τα χρώματα στις διαστάσεις κόκκινο-πράσινο-μπλε κυμαίνονται από 0 έως 255.
Γενικά, οι τιμές που μπορεί να πάρει μια διάσταση μπορεί να είναι πολύ περιορισμένες. Στα χρώματα είναι 256 (από 0 έως 255), αλλά σε άλλες περιπτώσεις μπορεί να είναι μόνο δύο. Π.χ. θα μπορούσαμε να έχουμε την οθόνη του υπολογιστή, και ένα αντίγραφό της στη μνήμη του υπολογιστή, οπότε κάθε pixel να έχει και μια επιπλέον (έκτη) διάσταση, που να παίρνει δύο τιμές: “ναι”, είναι στη φυσική οθόνη που βλέπουμε· και “όχι”, είναι στην οθόνη–αντίγραφο. Βλέπουμε οτι δεν είναι καν απαραίτητο να είναι αριθμοί οι τιμές μιας διάστασης. Π.χ. στο τελευταίο αυτό παράδειγμα, οι τιμές της έκτης διάστασης είναι “ναι” ή “όχι”. Άλλο παράδειγμα είναι οι ημέρες της εβδομάδας, που έχουν σαν τιμές συγκεκριμένες λέξεις, όπως Κυριακή, Δευτέρα, Τρίτη,... κλπ.
Ακόμη μία ιδιότητα των διαστάσεων μπορούμε να παρατηρήσουμε στο σημείο αυτό. Είναι δυνατό να έχουμε διαστάσεις που είναι “ανακυκλωμένες”, δηλαδή να σχηματίζουν ένα “βρόχο” (αγγλ.: “loop”), όπου μετά από την τελευταία (μέγιστη ή ελάχιστη) τιμή της διάστασης, οι τιμές να ανακυκλώνονται από την “άλλη πλευρά” (ελάχιστη ή μέγιστη) της διάστασης. Το προηγούμενο παράδειγμα, των ημερών της εβδομάδας, αποτελεί μια τέτοια ανακυκλωμένη διάσταση, εφόσον δεν υπάρχει “πρώτη” ή “τελευταία” ημέρα, αλλά κάθε ημέρα συνεχίζεται με μια επόμενη και έχει μια προηγούμενη. Σε όσους έχουν παίξει ποτέ το παλιό κλασικό παιχνίδι Pacman, η ιδέα της ανακύκλωσης τους είναι οικεία με διαφορετικό τρόπο, που φαίνεται στην παρακάτω εικόνα:
Το κινούμενο “pacman” στην παραπάνω εικόνα έχει μισο-βγει από αριστερά από το διάδρομο στο μέσον, και ταυτόχρονα εμφανίζεται να μισο-μπαίνει από δεξιά, σε διάδρομο που μοιάζει να ανακυκλώνει την κατακόρυφη διάσταση, τουλάχιστον σε μια συντεταγμένη. Αν φανταστούμε να μπορεί να γίνει αυτή η ανακύκλωση σε όλες τις συντεταγμένες της κατακόρυφης διάστασης, τότε η “πίστα” αυτού του είδους pacman θα μοιάζει με την επιφάνεια κυλίνδρου, αφού θα μπορούσαμε τυλίγοντάς την και κολλώντας τις δύο κατακόρυφες πλευρές να σχηματίσουμε κύλινδρο. Ακόμα και η οριζόντια διάσταση θα μπορούσε να είναι ανακυκλωμένη, οπότε αντί για κύλινδρο, το γεωμετρικό σχήμα που θα σχηματιζόταν θα ήταν αυτό του “λουκουμά” (ή ντόνατ, αυτού με την τρύπα στη μέση), ή “τόρου” όπως λέγεται στη γεωμετρία (ή ακριβέστερα στην τοπολογία), και που φαίνεται στην παρακάτω εικόνα.
Η συζήτηση περί ανακυκλωμένων διαστάσεων έχει σημασία στη φυσική. Σε κάποιες θεωρίες κβαντικής φυσικής, το σύμπαν-μας, εκτός από τις οικείες-μας τέσσερις “μακρο-διαστάσεις” (τρεις του χώρου και μία του χρόνου), έχει και άλλες “μικρο-διαστάσεις”, που είναι ανακυκλωμένες. Αυτά τα θέματα όμως είναι εκτός του εύρους της θεωρίας της σχετικότητας.
2.0.2 Η έννοια του ίσιου και του καμπύλου χώρου και διάστασης
Ίσως ο αναγνώστης να πιστεύει οτι γνωρίζει πολύ καλά τί είναι μια “ευθεία γραμμή”. Από το δημοτικό σχολείο ακόμα μαθαίνουμε έναν πολύ χρήσιμο (για το παρόν θέμα-μας) ορισμό: «ευθεία γραμμή είναι η συντομότερη απόσταση μεταξύ δύο σημείων». Σωστά. Μόνο που το τί είναι “συντομότερη απόσταση” δεν συμβαδίζει πάντα με την εικόνα της ευθείας γραμμής που σχηματίζουμε στο νου-μας από την εμπειρία-μας με τον περιβάλλοντα χώρο.
Την εικόνα της ευθείας γραμμής μας τη δίνει — κι αυτό μερικές φορές μας δίνεται σαν βοηθητική γνώση από το σχολείο — μια ακτίνα φωτός. Μπορεί επίσης να δοθεί το παράδειγμα μιας τεντωμένης κλωστής, αλλά επειδή η κλωστή έχει ένα κάποιο πάχος (ενώ η ευθεία της γεωμετρίας έχει πάχος ακριβώς μηδέν), και κυρίως επειδή η κλωστή έχει κάποιο — έστω ελαχιστότατο — βάρος, και άρα επηρεάζεται από τη βαρύτητα, δηλαδή καμπυλώνεται από αυτήν — οσοδήποτε αμελητέα κι αν είναι αυτή η καμπύλωση — γιαυτό οι δάσκαλοι προτιμούν το παράδειγμα της ακτίνας φωτός σαν πρότυπο ευθείας. Η ακτίνα φωτός, υποτίθεται, δεν καμπυλώνεται από τη βαρύτητα.
Αυτό που θα μάθουμε προχωρώντας αργότερα στη γενική σχετικότητα είναι οτι και το φως καμπυλώνεται από τη βαρύτητα. Ο λόγος είναι πολύ απλός, και μπορεί να εξηγηθεί ακόμα και σ’ αυτό το πρώιμο στάδιο. Γνωρίζουμε πως η βαρύτητα είναι υπεύθυνη για την έλξη μεταξύ των σωμάτων που έχουν μάζα. Έτσι η Γη, έχοντας μεγάλη μάζα, έλκει την κλωστή προς το κέντρο-της (προς τη διεύθυνση που εμείς αντιλαμβανόμαστε σαν “προς τα κάτω”).(*) Τώρα, το ζήτημα είναι οτι και το φως έχει ένα “ισοδύναμο μάζας”. Δεν ισχύει οτι το φως έχει μάζα, γιατί το φως είναι καθαρή ενέργεια. Αλλά η ενέργεια έχει ένα ισοδύναμο σε μάζα, λόγω της γνωστής σχέσης E = m·c2, όπου E η ενέργεια, m η μάζα, και c η ταχύτητα του φωτός — τύπος που προέρχεται από τη σχετικότητα, και που τον γνωρίζουν, εξ όψεως τουλάχιστον, ακόμα και τα παιδιά. Έτσι, όπως έλκεται βαρυτικά η μάζα, έτσι έλκεται και η ενέργεια, αφού η ενέργεια έχει ένα ισοδύναμο μάζας. Επομένως έλκεται — άρα καμπυλώνεται — από τη Γη και η ακτίνα του φωτός, έστω κι αν την καμπύλωση αυτή είναι εξαιρετικά δύσκολο να τη μετρήσουμε (αδύνατο με τα σημερινά τεχνικά μέσα). Άρα ούτε η ακτίνα φωτός αποτελεί πρότυπο της έννοιας “ευθεία γραμμή”, όχι εδώ στη Γη τουλάχιστον. Αλλά κι αν μεταφερθούμε στο διάστημα, και πάλι είναι αδύνατο να αποφύγουμε τα βαρυτικά πεδία, καθώς αυτά υφίστανται σε ολόκληρο το Γαλαξία. Πώς μπορούμε λοιπόν να μιλάμε για ευθείες γραμμές όταν δεν έχουμε ούτε ένα πρότυπό τους στο φυσικό κόσμο για να πούμε οτι ευθεία είναι ότι μοιάζει με εκείνο το σχήμα;
Όπως θα δούμε, η ταυτοποίηση αυτού που οπτικά αντιλαμβανόμαστε σαν “ευθεία” με την έννοια “συντομότερη απόσταση” δεν είναι σωστή, γιατί η συντομότερη απόσταση δεν είναι πάντα αυτό που νομίζουμε. Το φως πράγματι ακολουθεί πάντα τη συντομότερη απόσταση. Όταν καμπυλώνεται (από τη βαρύτητα) αυτό το κάνει γιατί αυτή η διαδρομή που ακολουθεί είναι η συντομότερη απόσταση, ενώ η (οπτικά) ευθεία γραμμή στην περίπτωση εκείνη δεν είναι η συντομότερη απόσταση. (Αυτά θα γίνουν ξεκάθαρα αργότερα, στη γενική σχετικότητα.) Έτσι, για τη συντομότερη απόσταση θα χρειαστεί να χρησιμοποιήσουμε έναν άλλο όρο: τη γεωδεσική γραμμή, που θα την ξεχωρίσουμε από αυτό που οπτικά μας φαίνεται σαν ευθεία. (Ο τόρος, στην εικόνα της προηγούμενης υποενότητας, είναι ζωγραφισμένος με γεωδεσικές γραμμές στην επιφάνειά του.)
Ας προχωρήσουμε ένα βήμα παραπέρα στην προηγούμενη ιδέα. Είπαμε οτι το φως μπορεί να καμπυλωθεί από τη βαρύτητα, και το κάνει αυτό γιατί ακολουθεί τη συντομότερη διαδρομή. Όσο πιο ισχυρή είναι η βαρύτητα, τόσο πιο μεγάλη η καμπύλωση του φωτός. Ας φανταστούμε τώρα οτι έχουμε έναν πολύ ισχυρό “βαρυτικό μαγνήτη”. Πρόκειται δηλαδή για μια πολύ μεγάλη συσσώρευση μάζας σε ένα χώρο π.χ. όχι μεγαλύτερο από ένα πορτοκάλι. Υπόψη οτι αυτό δεν αποτελεί κάτι το αδύνατο, καθώς κάθε μαύρη τρύπα είναι ένας πολύ ισχυρός βαρυτικός μαγνήτης, από τον οποίο δεν ξεφεύγει ούτε το φως· μόνο που οι διαστημικές μαύρες τρύπες είναι πολύ μεγαλύτερες από πορτοκάλια. Εμείς θα θεωρήσουμε οτι ο βαρυτικός μαγνήτης-μας είναι όχι μαύρη τρύπα, αλλά κομμάτι ύλης από αστέρα νετρονίων, ή κάτι ανάλογο, που έχει τεράστια πυκνότητα και επομένως πολύ ισχυρή βαρυτική έλξη. Έστω οτι ο μαγνήτης αυτός μπορεί να καμπυλώσει το φως με τρόπο που να είναι μετρήσιμος, ακόμη και οπτικά εμφανής, με αποτέλεσμα οι συντεταγμένες πάνω στην καμπυλωμένη ακτίνα φωτός να φαίνονται έτσι όπως παρουσιάζονται στο ακόλουθο διάγραμμα:

Η σημαντική ιδέα που πρέπει να κατανοήσουμε τώρα είναι οτι η παρουσία του “βαρυτικού μαγνήτη” (πορτοκαλί κύκλος στην εικόνα) δεν καμπυλώνει απλά μια ακτίνα φωτός, αλλά ολόκληρο το χώρο κοντά-του! Η παρουσία δηλαδή της μεγάλης μάζας καμπυλώνει τον τριδιάστατο χώρο γύρω-της. Έτσι εξηγείται και η θέση του “μαγνήτη” ως προς την καμπύλη: στο διδιάστατο επίπεδο της παρούσας σελίδας, η γραμμή μοιάζει μάλλον να απωθείται από το μαγνήτη, παρά να έλκεται. Πρέπει όμως να φανταστούμε το σχήμα σε τρεις διαστάσεις: είναι σαν ο “μαγνήτης” να είναι η τρύπα στο σιφώνιο ενός νεροχύτη, και η καμπύλη γραμμή να είναι η πορεία που θα ακολουθούσε ένα σφαιρίδιο (π.χ. γυάλινος βώλος) που έρχεται με ορισμένη ταχύτητα περίπου προς τη διεύθυνση του σιφωνίου, αλλά όχι ακριβώς προς αυτό· η τροχιά του σφαιριδίου τότε θα καμφθεί, ακολουθώντας την καμπύλωση της επιφάνειας του νεροχύτη κοντά στο σιφώνιο. Αυτό είναι που αποτυπώνεται στην παραπάνω εικόνα. Ότι όμως περιγράφηκε σε δύο διαστάσεις για την επιφάνεια του νεροχύτη, πρέπει να το φανταστούμε σε τρεις διαστάσεις για την περιοχή του χώρου κοντά στο “βαρυτικό μαγνήτη”.
Εδώ πρέπει να σταθούμε μια στιγμή για να κατανοήσουμε την ιδέα: την καμπύλωση του τριδιάστατου χώρου, γιατί με κάτι τέτοιο δεν είμαστε εξοικειωμένοι από την εμπειρία-μας.
Είμαστε θαυμάσια εξοικειωμένοι με καμπύλους μονοδιάστατους χώρους, γιατί κάθε καμπύλη που ζωγραφίζουμε σ’ ένα τετράδιο (όπως και αυτή του προηγούμενου διαγράμματος) είναι ακριβώς αυτό: ένας καμπύλος μονοδιάστατος χώρος. (Έχει μία μόνο διάσταση γιατί στη γειτονιά κάθε σημείου-του έχει μόνο μήκος, και δεν έχει ούτε πλάτος ούτε ύψος.)
Εξίσου εξοικειωμένοι είμαστε και με καμπύλους διδιάστατους χώρους, γιατί κάθε κοίλη ή κυρτή επιφάνεια, όπως η επιφάνεια μιας μπάλας (σφαίρας), ή ενός αβγού (ελλειψοειδούς), ή ενός τόρου (βλέπε εικόνα), κλπ., είναι χώρος καμπύλος και διδιάστατος. (Έχει δύο διαστάσεις γιατί στη γειτονιά κάθε σημείου-του έχει μόνο μήκος και πλάτος, αλλά όχι ύψος.)
Αλλά με καμπύλους τριδιάστατους χώρους δεν είμαστε καθόλου εξοικειωμένοι. Άλλωστε, γνωρίζουμε μόνο έναν τριδιάστατο χώρο: αυτόν το χώρο μέσα στον οποίο ζούμε και κινούμαστε.(*) Αυτός ο οικείος-μας χώρος μας φαίνεται “ίσιος”, “ευθύς”, “επίπεδος”. Ας σημειώσουμε και το οτι δεν έχουμε κατάλληλη λέξη. Το “ευθύς” το χρησιμοποιούμε για γραμμές (μία διάσταση)· το “επίπεδος” το χρησιμοποιούμε για επιφάνειες (δύο διαστάσεις)· αλλά για τις τρεις διαστάσεις δεν έχουμε κατάλληλο επίθετο, ακριβώς γιατί γνωρίζουμε ένα μόνο τριδιάστατο χώρο, και αυτός μας φαίνεται... “ίσιος”. (Γιατί “ίσιος”; Διότι κινούμενοι μέσα σ’ αυτόν το χώρο ελεύθερα, χωρίς να μας σπρώχνει κάποιος, δεν αισθανόμαστε καμμιά “φυγόκεντρη δύναμη” να δρα επάνω-μας, οπότε κινούμαστε σε ευθεία γραμμή. Ή τουλάχιστον έτσι μας φαίνεται.)
Στο σημείο αυτό λοιπόν, πρέπει να κατανοήσουμε οτι και ο οικείος-μας τριδιάστατος χώρος είναι δυνατό να καμπυλωθεί· και μάλιστα καμπυλώνεται παντού όπου υπάρχουν μάζες, υλικά σώματα δηλαδή. Μόνο που η καμπύλωση συνήθως είναι τόσο απειροελάχιστη που δεν μπορούμε να τη μετρήσουμε ούτε με τα ακριβέστερα όργανα της φυσικής. Χρειάζονται τεράστιες (για τα ανθρώπινα μέτρα) συγκεντρώσεις μάζας για να γίνει αισθητή η καμπύλωση του τριδιάστατου χώρου, και αυτό συμβαίνει στη γειτονιά των αστέρων, όπως ο Ήλιος, και ακόμα περισσότερο ειδικών αστέρων με εξαιρετική πυκνότητα, όπως οι αστέρες νετρονίων. (Και βέβαια ακόμα πιο πολύ στην περιοχή γύρω από τις μαύρες τρύπες.) Το αν μπορούμε ή όχι να μετρήσουμε την καμπύλωση όμως, είναι καθαρά θέμα τεχνολογίας. Δεν πρέπει να μας διαφεύγει οτι θεωρητικά ο χώρος καμπυλώνεται ακόμα και γύρω από έναν κόκκο σκόνης.
Συνοψίζοντας, βλέπουμε οτι επανακαθορίσαμε κάποιες έννοιες με τρόπο κάπως διαφορετικό από τον οικείο:
![]() Τις έννοιες “ίσιο”
και “καμπύλο”, τις οποίες γενικεύσαμε και στον τριδιάστατο χώρο.
Γνωρίζουμε οτι ίσιος μονοδιάστατος χώρος είναι η οικεία-μας ευθεία, αυτό
που “οπτικά” φαίνεται σαν ίσια γραμμή· ενώ καμπύλος μονοδιάστατος χώρος είναι
οποιαδήποτε γραμμή που δεν είναι ευθεία ούτε έχει τμήματα ευθειών.
Γνωρίζουμε επίσης οτι ίσιος
διδιάστατος χώρος είναι ένα επίπεδο, ενώ καμπύλος διδιάστατος χώρος
είναι οποιαδήποτε επιφάνεια που δεν είναι επίπεδο, ούτε έχει τμήματα
επιπέδων. Τώρα όμως είδαμε οτι ίσιος τριδιάστατος χώρος θα ήταν ο χώρος στον οποίον
κινούμαστε αν έλλειπαν τα βαρυτικά πεδία· στην πραγματικότητα είναι
καμπύλος (καμπυλώνεται από τα βαρυτικά πεδία), αλλά τόσο λίγο που εμείς τον
αντιλαμβανόμαστε σαν ίσιο.
Τις έννοιες “ίσιο”
και “καμπύλο”, τις οποίες γενικεύσαμε και στον τριδιάστατο χώρο.
Γνωρίζουμε οτι ίσιος μονοδιάστατος χώρος είναι η οικεία-μας ευθεία, αυτό
που “οπτικά” φαίνεται σαν ίσια γραμμή· ενώ καμπύλος μονοδιάστατος χώρος είναι
οποιαδήποτε γραμμή που δεν είναι ευθεία ούτε έχει τμήματα ευθειών.
Γνωρίζουμε επίσης οτι ίσιος
διδιάστατος χώρος είναι ένα επίπεδο, ενώ καμπύλος διδιάστατος χώρος
είναι οποιαδήποτε επιφάνεια που δεν είναι επίπεδο, ούτε έχει τμήματα
επιπέδων. Τώρα όμως είδαμε οτι ίσιος τριδιάστατος χώρος θα ήταν ο χώρος στον οποίον
κινούμαστε αν έλλειπαν τα βαρυτικά πεδία· στην πραγματικότητα είναι
καμπύλος (καμπυλώνεται από τα βαρυτικά πεδία), αλλά τόσο λίγο που εμείς τον
αντιλαμβανόμαστε σαν ίσιο.
Σε έναν ίσιο χώρο, οι διαστάσεις είναι κι αυτές συνήθως ίσιες· ενώ σε έναν καμπύλο χώρο, οι διαστάσεις είναι κι αυτές συνήθως καμπύλες, ακολουθώντας την καμπυλότητα του χώρου.
![]() Και
την έννοια “συντομότερη απόσταση”, που τη διαχωρίσαμε από την έννοια
“ευθεία”. Είπαμε οτι “ευθεία” παραμένει αυτό που οπτικά μας φαίνεται σαν
ευθεία (και ας σημειώσουμε οτι το “οπτικά ευθεία” ορίζεται με αυστηρά
μαθηματικό τρόπο: πρόκειται για τις λεγόμενες “γραμμικές εξισώσεις μιας
παραμέτρου”)· ενώ η συντομότερη απόσταση, όταν ο χώρος είναι καμπύλος,
δεν είναι ευθεία αλλά καμπύλη, που λέγεται γεωδεσική, και που το
είδος-της εξαρτάται από το είδος της καμπύλωσης του χώρου. Όταν ο χώρος είναι “ίσιος”,
τότε οι γεωδεσικές είναι όντως ευθείες. Και αυτός είναι ο λόγος που οι
ακτίνες φωτός μας φαίνονται ευθείες: επειδή, ενώ ο χώρος γύρω-μας είναι
απειροελάχιστα καμπύλος, εμάς μας φαίνεται ακριβώς ίσιος· έτσι
οι γεωδεσικές-του (που διαγράφονται από τις ακτίνες φωτός) μας φαίνονται
ακριβώς ευθείες (αλλά δεν είναι).
Και
την έννοια “συντομότερη απόσταση”, που τη διαχωρίσαμε από την έννοια
“ευθεία”. Είπαμε οτι “ευθεία” παραμένει αυτό που οπτικά μας φαίνεται σαν
ευθεία (και ας σημειώσουμε οτι το “οπτικά ευθεία” ορίζεται με αυστηρά
μαθηματικό τρόπο: πρόκειται για τις λεγόμενες “γραμμικές εξισώσεις μιας
παραμέτρου”)· ενώ η συντομότερη απόσταση, όταν ο χώρος είναι καμπύλος,
δεν είναι ευθεία αλλά καμπύλη, που λέγεται γεωδεσική, και που το
είδος-της εξαρτάται από το είδος της καμπύλωσης του χώρου. Όταν ο χώρος είναι “ίσιος”,
τότε οι γεωδεσικές είναι όντως ευθείες. Και αυτός είναι ο λόγος που οι
ακτίνες φωτός μας φαίνονται ευθείες: επειδή, ενώ ο χώρος γύρω-μας είναι
απειροελάχιστα καμπύλος, εμάς μας φαίνεται ακριβώς ίσιος· έτσι
οι γεωδεσικές-του (που διαγράφονται από τις ακτίνες φωτός) μας φαίνονται
ακριβώς ευθείες (αλλά δεν είναι).
Μία τελευταία έννοια μένει να ξεκαθαρίσουμε στο παρόν σημείο. Όταν λέμε, για παράδειγμα, οτι: «Έστω οτι ο χώρος είναι η διδιάστατη επιφάνεια ενός τόρου», εννοούμε οτι υποθέτουμε πως μόνο η επιφάνεια του τόρου είναι ο διδιάστατος χώρος όπου μπορεί να υπάρξει και να κινηθεί οτιδήποτε. (Εξυπακούεται επίσης οτι αυτό το “οτιδήποτε” είναι διδιάστατο.) Εφόσον λέμε οτι αυτός είναι “ο χώρος”, εννοούμε οτι δεν μπορεί να υπάρξει οτιδήποτε εκτός αυτού του χώρου, όπως π.χ. στο εσωτερικό του τόρου, ή στο εξωτερικό-του, γιατί — δοσμένης της υπόθεσης οτι αυτός (η επιφάνεια) είναι όλος κι όλος ο χώρος — δεν υπάρχει το “εκτός” αυτού του χώρου. Έτσι, στην υποθετική περίπτωση που μια ακτίνα φωτός πρέπει να κινηθεί στο διδιάστατο χώρο ενός τόρου, θα ακολουθήσει μια από τις γεωδεσικές γραμμές της επιφάνειάς του (βλ. διάγραμμα σε προηγούμενη υποενότητα), και όχι ευθεία γραμμή.
Κάτι ανάλογο μπορούμε να φανταστούμε για τον οικείο-μας τριδιάστατο χώρο· ή καλύτερα, τον τετραδιάστατο χωροχρόνο, όπως θα μάθουμε στα περί γενικής σχετικότητας: αν ο οικείος-μας χωροχρόνος είναι όλος κι όλος ο “χώρος” του σύμπαντος, δεν υπάρχει το “εκτός” αυτού του χώρου, δεν υφίσταται το “έξω από το σύμπαν”. Φυσικά, μπορεί η υπόθεση οτι ο οικείος-μας χωροχρόνος είναι όλο κι όλο που υπάρχει να είναι λάθος. Μπορεί να υπάρχει και άλλη (5η) μακρο-διάσταση, άγνωστη μέχρι τώρα, ώστε ο τετραδιάστατος χωροχρόνος (το “σύμπαν”) να υφίσταται εντός ενός άλλου, πενταδιάστατου χώρου, κλπ. Αυτά όμως είναι υποθέσεις χωρίς βάση στην παρατήρηση, που τις αναφέρουμε απλώς γιατί μας βοηθούν να κατανοήσουμε καλύτερα τις έννοιες “χώρος”, “διάσταση”, κλπ.
2.0.3 Η έννοια της μέτρησης μήκους και της μετρικής
Η Ε Ν Ο Τ Η Τ Α Α Υ Τ Η Θ Α Σ Υ Μ Π Λ Η Ρ Ω Θ Ε Ι Σ Τ Ο Μ Ε Λ Λ Ο Ν
Σ Υ Ν Ε Χ Ι Ζ Ε Τ Α Ι . . .
Σημειώσεις (με κλικ στο (^) μεταφέρεστε στο αντίστοιχο σημείο του κειμένου):
(^) Βλ., π.χ.: Relativity: the Special and the General Theory, από τον Albert Einstein, εκδόσεις Crown Trade Paperbacks, 15η έκδοση (1961), μετάφραση του Robert W. Lawson.
(^) Τα ονόματά τους στην ελληνική έχει επικρατήσει να προφέρονται “Μίκελσον” και “Μόρλεϊ”. Εδώ τα αποδίδουμε λίγο πιο πιστά στον τρόπο με τον οποίο τα προφέρουν οι Αμερικανοί.
(^) Όλοι μπορεί να έχουμε παρατηρήσει φαινόμενο μη συμβολής. Συμβαίνει π.χ. σε μια κουρτίνα με διπλό ύφασμα και πολύ ψιλή υφή, όπου βλέπουμε “κύματα” να σχηματίζονται. Τα “κύματα” αλλάζουν θέση καθώς κινείται η κουρτίνα. Ένα τέτοιο είδος κυμάτων περίμεναν να παρατηρήσουν οι Michelson και Morley.
(^) Ασφαλώς υπάρχουν άλλα ονόματα, φιλοσόφων και μαθηματικών κυρίως, που αναφέρονται όταν κάνει κανείς μια αναδρομή στο πώς αναδύθηκε ιστορικά η θεωρία της σχετικότητας· όπως ο Αυστριακός φιλόσοφος Ernst Mach (Ερνστ Μαχ), του 19ου αιώνα, οι ιδέες του οποίου επηρέασαν το νεαρό Αϊνστάιν· ο Γάλλος μαθηματικός, φυσικός, και φιλόσοφος της επιστήμης Henri Poincaré (Ανρί Πουανκαρέ), που “πλησίασε” τη σχετικότητα λίγο πιο πριν από τον Αϊνστάιν, χωρίς όμως να τη διατυπώσει ξεκάθαρα· ο Γερμανός μαθηματικός Hermann Minkowski (Χέρμαν Μινκόβσκι), καθηγητής του Αϊνστάιν, που (αργότερα, αφού ο Αϊνστάιν είχε δημοσιεύσει τα περί σχετικότητας) διατύπωσε τη “γεωμετρία Μινκόβσκι”, μέσω της οποίας η ειδική σχετικότητα απεικονίζεται γεωμετρικά — πράγμα που θα δούμε στη συνέχεια. Κανείς όμως από αυτούς δεν έπαιξε θεμελιακό, καθοδηγητικό, και ουσιαστικό ρόλο, όπως ο Αϊνστάιν.
(^) Πάντως αν ο Β μπορεί να δει έξω από το διαστημόπλοιό του, υπάρχουν παρατηρήσεις που μπορεί να κάνει για να καταλάβει οτι ο δικός-του χρόνος είναι διεσταλμένος. Μπορεί να παρατηρήσει, λόγω του φαινομένου Doppler, οτι τα αστέρια τα οποία αυτός πλησιάζει έχουν το φάσμα-τους περισσότερο μετατοπισμένο προς το ιώδες απ’ ότι θα έπρεπε, άρα τον πλησιάζουν με μεγάλη ταχύτητα, την οποία μπορεί να υπολογίσει και να βρει ίση με v. Αυτά όμως ξεφεύγουν από το το θέμα-μας.
(^) Όταν π.χ. κοιτάμε προς το γαλαξία της Ανδρομέδας, τον βλέπουμε όπως ήταν 2,5 εκατομμύρια χρόνια πριν (γιατί τόσο κάνει το φως-του να φτάσει ως εμάς). Εμείς τον κοιτάμε τώρα, αλλά τον βλέπουμε όπως ήταν στο παρελθόν. Ο παρατηρητής (αν υπάρχει) στο γαλαξία της Ανδρομέδας, στο δικό-του “τώρα”, βλέπει εμάς όπως ήμασταν 2,5 εκατομμύρια χρόνια πριν. (Άρα, παρεμπιπτόντως, δεν βλέπει το δικό-μας είδος ανθρώπου, αλλά τους αυστραλοπίθηκους — θεωρητικά όλα αυτά, ή: “πειράματα σκέψης”.) Το “τώρα” λοιπόν, είναι μεν σχετικό, αλλά και το σύμπαν έχει εξελιχθεί συνολικά, κατά τρόπο που το κάνει πολύ διαφορετικό από το “τότε” του χρόνου λίγο μετά από τη Μεγάλη Έκρηξη. Το σύμπαν είναι απόλυτα πιο διαφορετικό από το τότε. Άρα και ο χρόνος έχει “παρέλθει” συνολικά στο σύμπαν, κατά έναν απόλυτο τρόπο. Όλα αυτά είναι εκτός του εύρους της ειδικής σχετικότητας.
(^) Ο αστερισμός του Κενταύρου είναι ορατός από το νότιο ημισφαίριο. Ο Εγγύτατος, στον αστερισμό αυτό, δεν φαίνεται με το μάτι, φαίνονται όμως οι λαμπρότεροι δύο αστέρες Ρίγκιλ Κενταύρου Α και Β, σαν ένας αστέρας πρώτου μεγέθους. Ο Εγγύτατος είναι βαρυτικά “δεμένος” με τους δύο αυτούς αστέρες. Έτσι, οι αστέρες αυτοί αποτελούν ένα τριπλό σύστημα, που εμείς βλέπουμε με το μάτι σαν ένα μόνο λαμπρό αστέρι. Μόνο πολύ ισχυρά τηλεσκόπια μπορούν να ξεχωρίσουν το σύστημα στα συστατικά-του αστέρια.
(^) Ή «προς το κυανό». Η μετατόπιση των χρωμάτων προ το μπλε ή το κόκκινο δεν σχετίζεται με τη θεωρία της σχετικότητας, αλλά με το φαινόμενο Doppler.
(^) “Τριδιάστατος”, και όχι *“τρισδιάστατος”· όπως επίσης “διδιάστατος” και όχι *“δισδιάστατος”. Το πρόθεμα τρι- σημαίνει “αυτό που έχει τρεις συνιστώσες”, όπως: “τριφασικό ρεύμα” (και όχι *“τρισφασικό ρεύμα”)· ενώ το πρόθεμα τρισ- σημαίνει “τρεις φορές”, όπως: “τρισμέγιστος” (“τρεις φορές μεγάλος”, και όχι: *“τριμέγιστος”). Επίσης στη συνέχεια θα μιλάμε για τον “τετραδιάστατο” χώρο (και βέβαια όχι για τον *“τετρακισδιάστατο”).
(^) Στον προγραμματισμό, συνήθως, ο άξονας Y προχωράει προς μεγαλύτερα νούμερα (συντεταγμένες) από πάνω προς τα κάτω· οπότε η αρχή του συστήματος συντεταγμένων βρίσκεται στην πάνω-αριστερή γωνία της οθόνης, ή του παραθύρου.
(^) Επίσης, και η κλωστή έλκει τη Γη με την ίδια δύναμη· αλλά λόγω της τεράστιας διαφοράς μάζας μεταξύ-τους, η κλωστή κινείται με προφανή τρόπο προς τη Γη, ενώ η κίνηση της Γης προς την κλωστή δεν μπορεί να παρατηρηθεί ούτε με όργανα της πιο γόνιμης επιστημονικής φαντασίας.
(^) Δεν μπορούμε να φανταστούμε να συνυπάρχουν δύο τριδιάστατοι χώροι στο περιβάλλον-μας, γιατί η “απλοϊκή φυσική” και η γεωμετρία με τις οποίες έρχεται εφοδιασμένος ο εγκέφαλός μας από τη γέννηση ακόμα (χάρη στη βιολογική εξέλιξη) μας λένε οτι ο ένας τριδιάστατος χώρος, αυτός τον οποίο αντιλαμβανόμαστε γύρω-μας, καλύπτει “τα πάντα” προεκτεινόμενος μέχρι το άπειρο· επομένως πώς είναι δυνατό να υπάρξει και άλλος τριδιάστατος χώρος; Αν υπήρχε, θα “έμπαινε μέσα” στον οικείο-μας τριδιάστατο χώρο, και οι δύο χώροι θα αλληλοκάλυπταν πλήρως ο ένας τον άλλον (εφόσον και ο δεύτερος χώρος θα προεκτεινόταν έως το άπειρο)· άρα, καθώς θα αλληλοκαλύπτονταν 100%, θα ήσαν ένας και ο αυτός χώρος, όχι δύο. Αυτά μας λέει η “απλοϊκή φυσική του εργοστασίου παραγωγής-μας”.
Πίσω στη γενική σελίδα του Διαδικτυακού Επιστημονικού Πανεπιστημίου