ΔΙΔΑΣΚΑΛΕΙΟ ΕΠΙΣΤΗΜΟΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
ΤΑ ΔΕΔΟΜΕΝΑ ΠΡΟΗΓΟΥΝΤΑΙ· ΟΙ ΘΕΩΡΙΕΣ ΕΠΟΝΤΑΙ
Περί τίνος πρόκειται
Το Δ.Ε.Π. είναι ένας εικονικός χώρος (δηλαδή δεν έχει φυσική, αλλά μόνο διαδικτυακή υπόσταση) όπου γίνεται διακίνηση ιδεών με στόχο τη διάδοση της επιστημονικής γνώσης περί του φυσικού κόσμου (κατ’ αποκλειστικότητα), αλλά και της επιστημονικής παιδείας (τί είναι η επιστήμη, πώς λειτουργεί) προς όσους ενδιαφέρονται να αποκτήσουν τη γνώση και την παιδεία αυτή.
Το Δ.Ε.Π. δεν παρέχει κανένα πτυχίο, προς αναγνώριση ή μη. Στόχος δεν είναι η απόκτηση ενός “χαρτιού”, αλλά η απόκτηση γνώσης.
Ποιο σκοπό εξυπηρετεί
Υπάρχουν πολλοί Έλληνες με ενδιαφέροντα που ξεπερνούν την καθημερινότητα και αφορούν στην επιστήμη, τα οποία δεν μπορούν να ικανοποιήσουν λόγω του οτι στην Ελλάδα η τριτοβάθμια εκπαίδευση έχει εντελώς χρησιμοθηρικό χαρακτήρα και προορίζεται για τους απόφοιτους Λυκείου. Το Δ.Ε.Π. δίνει τη δυνατότητα σε όσους ενδιαφέρονται έχοντας σαν στόχο τη γνώση (χωρίς να αναμένουν από αυτήν άμεσα οικονομικά οφέλη) να μάθουν για το τί είναι ο κόσμος που μας περιβάλλει, από τί αποτελείται, πώς λειτουργεί, πώς εξελίσσεται, και προς τα πού οδεύει. Ο μόνος ηλικιακός περιορισμός στο Δ.Ε.Π. είναι οτι πρέπει να έχετε τελειώσει το Λύκειο. Αν ενδιαφέρεστε για τα βαθύτερα κίνητρα που οδήγησαν στη σύσταση του Δ.Ε.Π., διαβάστε αυτήν την παράγραφο.
Πώς λειτουργεί
Υπάρχει ο διδάσκων, και ο διδασκόμενος.* Ο διδάσκων “συναντά” το διδασκόμενο στο διαδίκτυο, σε συνομιλία που γίνεται πρόσωπο-με-πρόσωπο* (με χρήση Skype) και δουλεύουν μαζί επί του θέματος που έχει επιλέξει ο διδασκόμενος. Ο διδάσκων παραδίδει όση θεωρητική γνώση είναι απαραίτητη κατά την άποψή του, και ο διδασκόμενος συζητά τα όσα μέχρι στιγμής έμαθε, και παρουσιάζει τα θέματα πάνω στα οποία δούλεψε. Γίνεται συνεχής ανταλλαγή ιδεών μεταξύ διδάσκοντος και διδασκομένου, στην οποία ο μεν πρώτος έχει καθοδηγητικό ρόλο, ο δε δεύτερος ενεργό και όχι παθητικό ρόλο — στο βαθμό που του το επιτρέπει το υπόβαθρό του. Εκτός από το ηλεκτρονικό γραπτό υλικό που παρέχει ο διδάσκων στο διδασκόμενο υπό μορφή σημειώσεων, χρησιμοποιείται επίσης το Διαδίκτυο σαν πηγή πληροφοριών. Επίσης διδάσκεται η ασφαλής άντληση επιστημονικών πληροφοριών από αυτό.
Η συχνότητα των συναντήσεων καθορίζεται κυρίως από τη διαθεσιμότητα διδασκομένου και διδάσκοντα. Η μόνη προϋπόθεση είναι οι συναντήσεις να μην είναι τόσο σπάνιες ώστε ο διδασκόμενος να ξεχνά όσα εντωμεταξύ έμαθε, ούτε τόσο συχνές ώστε από τη μια μεριά να μη μπορεί ο διδάσκων να ανταποκριθεί στο φόρτο εργασίας, και από την άλλη ο διδασκόμενος να μην προλαβαίνει να αφομοιώσει τη γνώση που απέκτησε. Η μέχρι σήμερα εμπειρία δείχνει οτι συναντήσεις μιας ώρας ανά εβδομάδα είναι ικανοποιητικές καί για τα δύο μέρη, αλλά αυτό βέβαια είναι κάτι που εξαρτάται από την περίπτωση.
Πόσο στοιχίζει
Το Δ.Ε.Π. έχει συσταθεί και υπάρχει σε εθελοντική βάση. Για το λόγο αυτό οι συναντήσεις γίνονται δωρεάν, εφόσον όμως υπάρχουν διδάσκοντες που είναι διατεθειμένοι να διδάξουν δωρεάν αυτό που επιθυμεί ο διδασκόμενος.
Το “αντάλλαγμα” για τα μαθήματα στο Δ.Ε.Π. είναι συνήθως όχι οικονομικό, αλλά “σε είδος”. Ένας διδάσκων μπορεί να ζητήσει οικονομικό αντάλλαγμα από τον διδασκόμενο εφόσον έρθει σε συγκεκριμένη συμφωνία μαζί-του, όπου το “μπορεί” έχει την έννοια του “δεν απαγορεύεται” — αλλά και δεν ενθαρρύνεται. Όταν το αντάλλαγμα είναι σε είδος, τότε εξαρτάται από τις δυνατότητες, τα προσόντα, και τα ενδιαφέροντα του διδασκομένου. Το αντάλλαγμα αυτό μπορεί να είναι ένα από τα εξής:
-
Μετάφραση κάποιων παραγράφων ή λέξεων από ή προς ξένη γλώσσα.
-
Βοήθεια σε ερευνητική εργασία του διδάσκοντος.
-
Εργασία σχετιζόμενη με την αρχαία ελληνική γλώσσα.
-
κάτι άλλο — οτιδήποτε εξαρτώμενο από το εκπαιδευτικό υπόβαθρο του διδασκομένου, και τα ενδιαφέροντα του διδάσκοντος.
Κάποια από τα μικρο-ανταλλάγματα αυτά συνεισφέρουν και στην περαιτέρω ανάπτυξη του Δ.Ε.Π. Συνεπώς το Δ.Ε.Π. οικοδομείται εν μέρει και από τους ίδιους τους συμμετέχοντες σ’ αυτό.
Αρχή του Δ.Ε.Π. είναι οτι ο διδασκόμενος πρέπει να εισπράττει ελαφρώς περισσότερα απ’ όσα προσφέρει. Όσο για τους διδάσκοντες, η φιλοσοφία του Δ.Ε.Π. είναι οτι το οικονομικό όφελος δεν πρέπει να αποτελεί πρωταρχικό κίνητρο για το διδάσκοντα· αντίθετα, πρωταρχικό κίνητρο πρέπει να είναι η διάδοση της γνώσης και της επιστημονικής σκέψης, ενώ εκείνο για το διδασκόμενο οφείλει να είναι η απόκτηση και η αφομοίωσή της. (Βλ. περί κινήτρων σύστασης του Δ.Ε.Π.) Παράλληλα, γίνεται προσπάθεια ώστε η ιδέα του “προσπαθώ να προσφέρω περισσότερα απ’ όσα εισπράττω” να μεταδίδεται έμμεσα και στο διδασκόμενο ώστε να γίνει κτήμα-του.
Ποιο το κέρδος για σας
Μπορεί ν’ αναρωτιέστε τί έχετε να κερδίσετε από την παρακολούθηση μαθημάτων. Είναι δυνατόν ποτέ να έχετε οικονομικό όφελος;
Λέγεται οτι κάποιος που είχε μόλις αρχίσει να μαθαίνει γεωμετρία ρώτησε τον Ευκλείδη: «Και τί έχω να κερδίσω εγώ από αυτά τα θεωρήματα που μαθαίνω;» Τότε ο Ευκλείδης στράφηκε σ’ ένα δούλο που στεκόταν εκεί κοντά και του είπε: «Παιδί, δώσε σ’ αυτόν τον άνθρωπο τρεις δραχμές, αφού θέλει να έχει κάποιο κέρδος από τη γεωμετρία!»
Παρά την αφοπλιστική όμως απάντηση του Ευκλείδη, και παρόλο που, όπως τονίστηκε παραπάνω, η φιλοσοφία του Δ.Ε.Π. είναι πως σ’ αυτό αποτείνονται όσοι έχουν σαν στόχο τη γνώση και όχι το κέρδος, είναι πράγματι δυνατό να έχετε όφελος στο μέλλον, αλλά με πολύ έμμεσο τρόπο. Ο λόγος είναι οτι η γνώση βοηθά τον άνθρωπο να παίρνει ορθές αποφάσεις. Το είδος της γνώσης που προσφέρει το Δ.Ε.Π. — όπως εξηγείται στην παράγραφο αυτή — θα σας βοηθήσει να οργανώσετε πιο μεθοδικά τον τρόπο που ζείτε και να παίρνετε αποφάσεις περισσότερο ορθολογικές παρά παρορμητικές, εκεί βέβαια όπου ο ορθολογισμός είναι απαραίτητος ή χρήσιμος. Πιο γενικά, η γνώση είναι ένα εφόδιο που κάνει τον άνθρωπο να αισθάνεται πιο ολοκληρωμένος και πιο σίγουρος για τον εαυτό-του και για το μέλλον-του· και αυτό ασφαλώς επιφέρει με έμμεσο τρόπο πολλαπλά οφέλη.
Προσφερόμενα μαθήματα
Τα μαθήματα χωρίζονται σε επιστημονικά πεδία, κατά τον παραδοσιακό τρόπο. Φυσικά, υπάρχουν κάποια προαπαιτούμενα για πολλά από τα μαθήματα. Δεν μπορείτε π.χ. να ξεκινήσετε να μαθαίνετε περί κοσμολογίας χωρίς να γνωρίζετε ούτε περί θεωρίας της σχετικότητας, ούτε περί μη Ευκλείδειων γεωμετριών. Τα προαπαιτούμενα σημειώνονται παρακάτω σε δύο διαβαθμίσεις: ΥΠ, που σημαίνει “Υποχρεωτικό Προαπαιτούμενο”, και ΠΠ, που σημαίνει “Προτεινόμενο Προαπαιτούμενο”. Εντούτοις είναι δυνατό να είναι προαπαιτούμενο όχι ολόκληρο ένα μάθημα, αλλά μόνο ένα μέρος αυτού. Ο διδάσκων στην πρώτη συνάντηση εξετάζει το βάθος και το εύρος των προαπαιτούμενων γνώσεων του διδασκομένου, και είτε ξεκινά με ανασκόπησή τους, είτε συνιστά τη μελέτη άλλου μαθήματος που παρέχει τη γνώση των προαπαιτούμενων. Υπόψη οτι υπάρχει ένα μάθημα, το Ε1, που είναι προαπαιτούμενο όλων.
Το Δ.Ε.Π. παρέχει γνώσεις στα παρακάτω
επιστημονικά πεδία και υποπεδία. Ο κάθε κύκλος μαθημάτων αντιστοιχεί
συνήθως σε ένα υποπεδίο. Κάνοντας κλικ στο υποπεδίο (όπου υπάρχει
σύνδεσμος) βλέπετε αναλυτικά τα περιεχόμενα του μαθήματος. Κάνοντας κλικ
όπου υπάρχει το εικονίδιο αυτό
![]() μεταφέρεστε σε αναλυτικές σημειώσεις του μαθήματος. Με το εικονίδιο αυτό
μεταφέρεστε σε αναλυτικές σημειώσεις του μαθήματος. Με το εικονίδιο αυτό
![]() μεταφέρεστε σε ιστοσελίδα που περιέχει λογισμικό κατάλληλο για το
μάθημα. Τέλος, με το εικονίδιο
αυτό
μεταφέρεστε σε ιστοσελίδα που περιέχει λογισμικό κατάλληλο για το
μάθημα. Τέλος, με το εικονίδιο
αυτό
![]() (όταν
εμφανίζεται μετά από τον τίτλο του μαθήματος) μεταφέρεστε σε
ιστοσελίδα όπου μπορείτε να ελέγξετε τις γνώσεις-σας, και αν πρόκειται
για προαπαιτούμενο, να “περάσετε” έτσι την απαίτηση του προαπαιτούμενου,
σε συνεννόηση βέβαια με το διδάσκοντα.
(όταν
εμφανίζεται μετά από τον τίτλο του μαθήματος) μεταφέρεστε σε
ιστοσελίδα όπου μπορείτε να ελέγξετε τις γνώσεις-σας, και αν πρόκειται
για προαπαιτούμενο, να “περάσετε” έτσι την απαίτηση του προαπαιτούμενου,
σε συνεννόηση βέβαια με το διδάσκοντα.
 Αστρονομία
Αστρονομία
 Βιολογία
Βιολογία
-
Β2
 Ταξινόμηση Ειδών
(ΠΠ: Β1)
Ταξινόμηση Ειδών
(ΠΠ: Β1) -
Β3 Κύτταρο – Γονίδια (ΠΠ: Β1)
-
Β4 Εξέλιξη Ειδών (ΥΠ: Β1· ΠΠ: Β2, Β3)
-
Β5 Εξέλιξη Ανθρώπου & Κοινωνιών (ΥΠ: Β1· ΠΠ: Β2, Β3, Β4)
 Γλωσσολογία
Γλωσσολογία
-
Γ1
 Θεμελιώδεις Αρχές
(είναι ΥΠ όλων των Γ)
Θεμελιώδεις Αρχές
(είναι ΥΠ όλων των Γ) -
Γ3 Μορφολογία
-
Γ4
 Συντακτικό
Συντακτικό -
Γ7 Εφαρμογή: Ιδιότητες της Αρχαίας Ελληνικής (ΠΠ: Γ2, Γ3, Γ4)
-
Γ8 Εφαρμογή: Ιδιότητες της Αγγλικής (ΠΠ: Γ2, Γ3)
 Επιστημονικές Βάσεις
Επιστημονικές Βάσεις
-
Ε1
 Επιστημονική Μέθοδος & Παραδοχές
Επιστημονική Μέθοδος & Παραδοχές
 (είναι
ΥΠ
πάντων εκτός Ε2)
(είναι
ΥΠ
πάντων εκτός Ε2)
 Κοσμολογία
Κοσμολογία
-
Κ1 Εξέλιξη Σύμπαντος (ΥΠ: Μ3, Φ2, Φ3· ΠΠ: Α2)
 Μαθηματικά
Μαθηματικά
-
Μ1
 Αποδεικτική Μέθοδος (είναι
ΥΠ όλων των Μ εκτός των Μ10 και Μ11)
Αποδεικτική Μέθοδος (είναι
ΥΠ όλων των Μ εκτός των Μ10 και Μ11) -
Μ2 Λογική
-
Μ11 Αριθμητική Ανάλυση (ΥΠ: Μ4, Υ2· ΠΠ: Μ5)
 Νοολογία
Νοολογία
-
Ν1
 Εισαγωγή στη Νοολογία (είναι ΥΠ όλων
των Ν)
Εισαγωγή στη Νοολογία (είναι ΥΠ όλων
των Ν) -
Ν3 Εγκέφαλος – Νευρώνες (ΠΠ: Β4)
-
Ν4
 Σχέση Νου –
Εγκεφάλου (ΥΠ: Ν3·
ΠΠ: Ν2)
Σχέση Νου –
Εγκεφάλου (ΥΠ: Ν3·
ΠΠ: Ν2) -
Ν5 Αρχιτεκτονική Νου κατά Hofstadter (ΥΠ: Ν2)
 Υπολογιστές
Υπολογιστές
-
Υ1 Θεμελιώδεις Έννοιες (είναι ΥΠ όλων των Υ)
-
Υ3 Δομές Δεδομένων (ΥΠ: Υ2)
-
Υ4 Είδη Γλωσσών Προγραμματισμού (ΥΠ: Υ2)
-
Υ5
 Αυτόματα – Τυπικές Γλώσσες –
Υπολογισιμότητα (ΥΠ: M1, Μ2, Μ7, Υ2·
ΠΠ: Υ3)
Αυτόματα – Τυπικές Γλώσσες –
Υπολογισιμότητα (ΥΠ: M1, Μ2, Μ7, Υ2·
ΠΠ: Υ3) -
Υ6
 Κυτταρικά Αυτόματα – Τεχνητή Ζωή
(ΥΠ: Υ2)
Κυτταρικά Αυτόματα – Τεχνητή Ζωή
(ΥΠ: Υ2) -
Υ7 Τεχνητή Νοημοσύνη (ΥΠ: Υ2· ΠΠ: Μ2)
-
Υ8
 Εφαρμογή: Ανάπτυξη Συστήματος
Αυτόματων Αποδείξεων (ΥΠ: Μ2, Υ2·
ΠΠ: Μ3, Υ3, Υ4, Υ7)
Εφαρμογή: Ανάπτυξη Συστήματος
Αυτόματων Αποδείξεων (ΥΠ: Μ2, Υ2·
ΠΠ: Μ3, Υ3, Υ4, Υ7)
 Φυσική
Φυσική
-
Φ1
 Θεμελιώδεις Αρχές
και Εξέλιξη Φυσικής (είναι ΥΠ όλων των Φ)
Θεμελιώδεις Αρχές
και Εξέλιξη Φυσικής (είναι ΥΠ όλων των Φ) -
Φ2
 Ειδική Σχετικότητα
και Στοιχεία Γενικής Σχετικότητας
(ΠΠ: Μ3)
Ειδική Σχετικότητα
και Στοιχεία Γενικής Σχετικότητας
(ΠΠ: Μ3)
Ποια είναι τα βαθύτερα κίνητρα πίσω από τη σύσταση του Δ.Ε.Π.
Πολλοί Έλληνες αρκετά συχνά παραπονούνται για τη χαοτική κατάσταση και ανοργανωσιά που επικρατεί στην Ελλάδα, ουσιαστικά σε όλες τις εκφάνσεις του βίου — δημόσιου και ιδιωτικού — και σε όλα τα επίπεδα: από τους επικεφαλής της πολιτικής ζωής, μέχρι αυτούς που μοχθούν για ένα μεροκάματο. Σχεδόν κανείς δεν φαίνεται να γνωρίζει πώς να κάνει αυτό που κάνει, οργανωμένα και συστηματικά. Όσοι έχουν ζήσει στο εξωτερικό έχουν δει τη διαφορετική οργάνωση που υπάρχει σε χώρες της Δυτικής και Κεντρικής Ευρώπης, στην Αυστραλία, και στις Η.Π.Α. — χώρες με οργάνωση σαφώς ανώτερη από την εγχώρια — όπως και το χάος και την αναρχία που επικρατεί σε χώρες ανατολικά και ιδίως νότια της Ελλάδας. Γιατί συμβαίνει αυτό; Είναι απλά ζήτημα χρημάτων; Γιατί όμως υπάρχουν τα χρήματα σε κάποια μέρη και όχι σε άλλα; Γιατί κάποιοι λαοί κατάφεραν ν’ αναπτυχθούν και να οργανωθούν καλύτερα από άλλους; Η απάντηση στα ερωτήματα αυτά είναι σύνθετη (βλ. μάθημα Β5: Εξέλιξη Ανθρώπου & Κοινωνιών, του Δ.Ε.Π.), αλλά το ερώτημα που πρέπει να μας απασχολεί ιδιαίτερα όλους είναι: δεν αξίζουμε εμείς οι Έλληνες μια ζωή καλύτερα οργανωμένη, με λιγότερο χάος, με πιο πολλή σιγουριά για το μέλλον, με γνώση του προς τα πού βαδίζουμε, με επαγγελματισμό σ’ αυτό με το οποίο ασχολούμαστε; Τί έχουν οι Αμερικανοί και οι Δυτικοευρωπαίοι που δεν το έχουμε εμείς, αλλά που θα μπορούσαμε να το αποκτήσουμε;
Ένα απ’ αυτά που έχουν είναι η
διαφορά της νοοτροπίας![]() · μια νοοτροπία που απέκτησαν κατά τους
προηγούμενους αιώνες, κυρίως σαν αποτέλεσμα του
Διαφωτισμού, ενός κινήματος
με βαθύτατες αρχαιοελληνικές ρίζες, όπως γίνεται
κατανοητό ιδίως στο μάθημα
Ε2 του Δ.Ε.Π. Όσο αναπτυσσόταν ο Διαφωτισμός
στην Ευρώπη εμείς στην Ελλάδα ήμασταν στα βουνά, σε ρόλους αρματωλών
και κλεφτών. Ο Διαφωτισμός πέρασε “ξώφαλτσα” από μας, χωρίς να μας
αγγίξει. Το βασικό στοιχείο που ενστάλαξε ο Διαφωτισμός στο νου των
κατοίκων της Δύσης του 17ου, 18ου,
και 19ου αιώνα ήταν ο ορθολογισμός,
δηλαδή η εμπιστοσύνη στη λογική σκέψη για τη λήψη αποφάσεων,
και κατά συνέπεια η εμπιστοσύνη στην επιστήμη,
που είναι ο καρπός της ορθολογικής σκέψης. Σαν
αποτέλεσμα της ορθολογικής σκέψης έρχονται άλλες αρετές σε μια κοινωνία,
όπως η αξιοκρατία· η πραγματική και ανεξάρτητη δικαιοσύνη·
η εκλογή αντιπροσώπων με βάση το ακέραιο του χαρακτήρα και τις
πολιτικές ικανότητές τους, και όχι με βάση την τηλεοπτική δημοτικότητά
τους, ή την αφοσίωσή τους στο κόμμα· κ.ά. Στην Ελλάδα έχουμε τεράστιο
έλλειμμα ορθολογισμού, άρα και έλλειμμα οργάνωσης. Όλα τα υπόλοιπα
ελλείμματα που τυχαίνει να έχουμε (π.χ., το οικονομικό έλλειμμα, ή αυτό
της δημοκρατίας, ή της αξιοκρατίας, ή της έλλειψης εργασιακής προοπτικής
των νέων, κλπ.), προέρχονται από το βασικό έλλειμμα της ορθολογικής
σκέψης
· μια νοοτροπία που απέκτησαν κατά τους
προηγούμενους αιώνες, κυρίως σαν αποτέλεσμα του
Διαφωτισμού, ενός κινήματος
με βαθύτατες αρχαιοελληνικές ρίζες, όπως γίνεται
κατανοητό ιδίως στο μάθημα
Ε2 του Δ.Ε.Π. Όσο αναπτυσσόταν ο Διαφωτισμός
στην Ευρώπη εμείς στην Ελλάδα ήμασταν στα βουνά, σε ρόλους αρματωλών
και κλεφτών. Ο Διαφωτισμός πέρασε “ξώφαλτσα” από μας, χωρίς να μας
αγγίξει. Το βασικό στοιχείο που ενστάλαξε ο Διαφωτισμός στο νου των
κατοίκων της Δύσης του 17ου, 18ου,
και 19ου αιώνα ήταν ο ορθολογισμός,
δηλαδή η εμπιστοσύνη στη λογική σκέψη για τη λήψη αποφάσεων,
και κατά συνέπεια η εμπιστοσύνη στην επιστήμη,
που είναι ο καρπός της ορθολογικής σκέψης. Σαν
αποτέλεσμα της ορθολογικής σκέψης έρχονται άλλες αρετές σε μια κοινωνία,
όπως η αξιοκρατία· η πραγματική και ανεξάρτητη δικαιοσύνη·
η εκλογή αντιπροσώπων με βάση το ακέραιο του χαρακτήρα και τις
πολιτικές ικανότητές τους, και όχι με βάση την τηλεοπτική δημοτικότητά
τους, ή την αφοσίωσή τους στο κόμμα· κ.ά. Στην Ελλάδα έχουμε τεράστιο
έλλειμμα ορθολογισμού, άρα και έλλειμμα οργάνωσης. Όλα τα υπόλοιπα
ελλείμματα που τυχαίνει να έχουμε (π.χ., το οικονομικό έλλειμμα, ή αυτό
της δημοκρατίας, ή της αξιοκρατίας, ή της έλλειψης εργασιακής προοπτικής
των νέων, κλπ.), προέρχονται από το βασικό έλλειμμα της ορθολογικής
σκέψης![]() ·
ένα έλλειμμα που έχει σαν αποτέλεσμα τη λήψη λανθασμένων αποφάσεων από
όλους και για όλα, σε πάμπολλες στιγμές της ζωής που ζούμε.
Στους δύσκολους καιρούς που περνά η Ελλάδα,
οι περισσότεροι Έλληνες είναι ανίκανοι να διαμορφώσουν αντικειμενική
άποψη για το πού βρισκόμαστε και προς τα πού βαδίζουμε, με αποτέλεσμα να
διατυπώνουν κραυγές*
αντί για σκέψεις, παρορμητικά αντί ορθολογικά,
συναισθηματικά αντί ψυχρά και αντικειμενικά, προσπαθώντας να αντιληφθούν
το μέλλον μέσω ιδεοληψιών του παρελθόντος. Τίποτα από αυτά δεν
προοιωνίζεται κάτι το καλό για τον τόπο.
·
ένα έλλειμμα που έχει σαν αποτέλεσμα τη λήψη λανθασμένων αποφάσεων από
όλους και για όλα, σε πάμπολλες στιγμές της ζωής που ζούμε.
Στους δύσκολους καιρούς που περνά η Ελλάδα,
οι περισσότεροι Έλληνες είναι ανίκανοι να διαμορφώσουν αντικειμενική
άποψη για το πού βρισκόμαστε και προς τα πού βαδίζουμε, με αποτέλεσμα να
διατυπώνουν κραυγές*
αντί για σκέψεις, παρορμητικά αντί ορθολογικά,
συναισθηματικά αντί ψυχρά και αντικειμενικά, προσπαθώντας να αντιληφθούν
το μέλλον μέσω ιδεοληψιών του παρελθόντος. Τίποτα από αυτά δεν
προοιωνίζεται κάτι το καλό για τον τόπο.
Αυτό το έλλειμμα ορθολογισμού στην
Ελλάδα προσπαθεί να καλύψει το Δ.Ε.Π. Δυστυχώς δεν μπορούν να δοθούν
άμεσες και δραστικές λύσεις στο “ελληνικό πρόβλημα”. Δεν είναι δυνατό το
Δ.Ε.Π. — ή όποια άλλη παρόμοια προσπάθεια — να αλλάξει μέσα σε μερικά
χρόνια νοοτροπίες αιώνων. Τον ορθολογισμό δεν μπορεί να
τον προμηθευτεί κανείς στο σούπερ μάρκετ. Πρέπει να τον αποκτήσει με κόπο,
και ο μόνος σίγουρος τρόπος είναι με το να εξοικειωθεί με την
ορθολογική επιστημονική σκέψη, μέσω εργασίας σε κάποιο επιστημονικό πεδίο. Αυτό
είναι το “όραμα” του Δ.Ε.Π.: πως με την καλύτερη κατανόηση και χρήση
της ορθολογικής σκέψης — σε βάθος χρόνου βέβαια — θα έρθει και η
καλυτέρευση της οργάνωσης της ζωής στην Ελλάδα, και θα βελτιωθούν οι
περισσότερες στρεβλές καταστάσεις που σήμερα διαπιστώνουμε
πως μας
ταλαιπωρούν. Η ιδέα αυτή μπορεί να είναι σωστή, μπορεί και
λάθος![]() · όμως αυτό για σας δεν έχει καμία
σημασία. Η παράγραφος αυτή εξηγεί ποια είναι τα κίνητρα της
σύστασης του Δ.Ε.Π. Εσάς αυτό που πρέπει να σας απασχολεί —
ως ορθολογικά σκεπτόμενους — είναι το
αποτέλεσμα, που είναι οτι υπάρχει αυτός ο φορέας, το Δ.Ε.Π., που
προσφέρεται να σας δώσει εκείνη τη γνώση που ελπίζουμε πως
επιθυμούσατε ανέκαθεν να αποκτήσετε.
· όμως αυτό για σας δεν έχει καμία
σημασία. Η παράγραφος αυτή εξηγεί ποια είναι τα κίνητρα της
σύστασης του Δ.Ε.Π. Εσάς αυτό που πρέπει να σας απασχολεί —
ως ορθολογικά σκεπτόμενους — είναι το
αποτέλεσμα, που είναι οτι υπάρχει αυτός ο φορέας, το Δ.Ε.Π., που
προσφέρεται να σας δώσει εκείνη τη γνώση που ελπίζουμε πως
επιθυμούσατε ανέκαθεν να αποκτήσετε.
Ποιοι είμαστε: διδακτικό προσωπικό
Μόνιμος διδάσκων είναι ο ιδρυτής του Δ.Ε.Π., και συγγραφέας της παρούσας σελίδας. Αυτός λειτουργεί και ως συντονιστής των υπόλοιπων διδασκόντων, οι οποίοι συστήνονται στους διδασκομένους ανά περίπτωση μαθήματος και διαθεσιμότητάς τους κατά τη συγκεκριμένη χρονική στιγμή. Ήτοι, οι υπόλοιποι διδάσκοντες εμφανίζονται όταν υπάρχει διδασκόμενος που δηλώνει ενδιαφέρον σε κάποιο μάθημα το οποίο ο διδάσκων έχει δηλώσει πως μπορεί να διδάξει.
Πώς να δηλώσετε ενδιαφέρον για συμμετοχή
 Ως διδασκόμενοι:
Ως διδασκόμενοι:
Στείλτε email στη διεύθυνση dep.science@gmail.com με θέμα «ΔΙΔΑΣΚΟΜΕΝΟΣ», και εξηγείστε με όσα λόγια θέλετε ποιοι είστε και τί επιθυμείτε να μάθετε από τον κύκλο μαθημάτων που προσφέρονται· αν το θεωρείτε χρήσιμο περιγράψτε επίσης και το λόγο για τον οποίο επιθυμείτε τη μάθηση. Θα ακολουθήσει συνεννόηση μέσω της οποίας θα διαπιστώσουμε κατά πόσο μπορούμε να σας βοηθήσουμε να αποκτήσετε γνώση του πεδίου της προτίμησής σας.
Παρακαλούμε πολύ, στα μηνύματά σας χρησιμοποιείτε ελληνικούς χαρακτήρες. Μη σπαταλάτε άδικα χρόνο με μηνύματα pu ine gramena se greeklish, τα οποία αγνοούνται από το Δ.Ε.Π. (Το λόγο θα τον καταλάβετε με τη συμπλήρωση ικανού αριθμού μαθημάτων.) — Ευχαριστούμε για την κατανόηση.
 Ως διδάσκοντες:
Ως διδάσκοντες:
Μπορεί να είστε γνώστες σε βάθος κάποιου επιστημονικού θέματος (ή θεμάτων), που είτε περιλαμβάνεται ήδη στον κύκλο μαθημάτων του Δ.Ε.Π. είτε όχι. Μπορεί να επιθυμείτε και σεις να μεταδώσετε τις γνώσεις που έχετε. Αν συμφωνείτε με τη φιλοσοφία του Δ.Ε.Π., στείλτε email στη διεύθυνση dep.science@gmail.com με θέμα «ΔΙΔΑΣΚΩΝ», και εξηγείστε τις λεπτομέρειες περί του τί προτίθεστε να διδάξετε. Πριν από οποιαδήποτε συμφωνία θα υπάρξει οπωσδήποτε αξιολόγηση της ποιότητας, τόσο των γνώσεών σας, όσο και της διδακτικής ικανότητάς σας. Δείτε αμέσως παρακάτω: «Παραλειπόμενοι τομείς: τί δεν διδάσκεται στο Δ.Ε.Π.» Το οποιοδήποτε οικονομικό όφελος (έστω των μηδαμινών “διδάκτρων” του Δ.Ε.Π.) πηγαίνει εξ’ ολοκλήρου (100%) σ’ εσάς.
Παραλειπόμενοι τομείς: τί δεν διδάσκεται στο Δ.Ε.Π.
![]() Η ιατρική επιστήμη· πιστεύουμε οτι η ιατρική είναι ένας
τελείως εξειδικευμένος, ανθρωποκεντρικός τομέας, δηλαδή
ασχολείται με τη φυσιολογία του ανθρώπινου σώματος,
που είναι σημαντικό θέμα για μας μεν, ασήμαντο
μέρος της φύσης δε. Επίσης, για να γίνει
σωστή χρήση ιατρικών γνώσεων απαιτούνται πάρα πολλά χρόνια σχετικής και εξειδικευμένης εκπαίδευσης, ενώ οι επιφανειακές
γνώσεις μπορούν να αποβούν μοιραίες για την υγεία των ανθρώπων. Συνεπώς
η ιατρική καλύτερα να αφήνεται στη δικαιοδοσία των πραγματικών γιατρών.
Εντούτοις, μπορεί σαν γιατρός να είστε σε θέση να διδάξετε κάποια θέματα
βιολογίας, βιοχημείας, ή
χημείας. Επικοινωνείστε στο dep.science@gmail.com
για περαιτέρω συνεννόηση.
Η ιατρική επιστήμη· πιστεύουμε οτι η ιατρική είναι ένας
τελείως εξειδικευμένος, ανθρωποκεντρικός τομέας, δηλαδή
ασχολείται με τη φυσιολογία του ανθρώπινου σώματος,
που είναι σημαντικό θέμα για μας μεν, ασήμαντο
μέρος της φύσης δε. Επίσης, για να γίνει
σωστή χρήση ιατρικών γνώσεων απαιτούνται πάρα πολλά χρόνια σχετικής και εξειδικευμένης εκπαίδευσης, ενώ οι επιφανειακές
γνώσεις μπορούν να αποβούν μοιραίες για την υγεία των ανθρώπων. Συνεπώς
η ιατρική καλύτερα να αφήνεται στη δικαιοδοσία των πραγματικών γιατρών.
Εντούτοις, μπορεί σαν γιατρός να είστε σε θέση να διδάξετε κάποια θέματα
βιολογίας, βιοχημείας, ή
χημείας. Επικοινωνείστε στο dep.science@gmail.com
για περαιτέρω συνεννόηση.
![]() Οι ειδικότητες μηχανικών· παραδείγματος χάρη, αν είστε
πολιτικός μηχανικός, χημικός μηχανικός, ηλεκτρολόγος μηχανικός,
μηχανολόγος μηχανικός, αρχιτέκτονας, ναυπηγός, κλπ., δεν μπορείτε να
διδάξετε την καθαυτό ειδικότητά σας μέσω του Δ.Ε.Π. Ο λόγος είναι οτι η
ειδικότητά σας αφορά σε πρακτική χρήση επιστημονικών γνώσεων, και
όχι σε απόκτηση της θεμελιώδους
εκείνης επιστημονικής γνώσης που βοηθά στην κατανόηση του φυσικού
κόσμου. Σημειώστε οτι ένας από τους στόχους του Δ.Ε.Π. είναι να βοηθήσει
τον διδασκόμενο να κατανοήσει το φυσικό κόσμο, και η μηχανική των
διαφόρων τομέων δεν έχει αυτόν το σκοπό. Εξαίρεση αποτελεί η λεγόμενη
“επιστήμη υπολογιστών” (που είναι ουσιαστικά μια μηχανική αλλά με
λογισμικό, όχι με υλικό μέσο), γιατί η γνώση της χρήσης υπολογιστών
επιτρέπει την εκτέλεση “πειραμάτων” (εικονικών έστω) μέσω των οποίων
είτε επαληθεύονται είτε
απορρίπτονται επιστημονικές υποθέσεις. Εντούτοις, μπορεί σαν μηχανικός
να είστε σε θέση να διδάξετε επιστήμες που βρίσκονται στο υπόβαθρο των
γνώσεών σας — π.χ., φυσική, χημεία, μαθηματικά, κλπ. Επικοινωνείστε στο
dep.science@gmail.com για περαιτέρω
συνεννόηση.
Οι ειδικότητες μηχανικών· παραδείγματος χάρη, αν είστε
πολιτικός μηχανικός, χημικός μηχανικός, ηλεκτρολόγος μηχανικός,
μηχανολόγος μηχανικός, αρχιτέκτονας, ναυπηγός, κλπ., δεν μπορείτε να
διδάξετε την καθαυτό ειδικότητά σας μέσω του Δ.Ε.Π. Ο λόγος είναι οτι η
ειδικότητά σας αφορά σε πρακτική χρήση επιστημονικών γνώσεων, και
όχι σε απόκτηση της θεμελιώδους
εκείνης επιστημονικής γνώσης που βοηθά στην κατανόηση του φυσικού
κόσμου. Σημειώστε οτι ένας από τους στόχους του Δ.Ε.Π. είναι να βοηθήσει
τον διδασκόμενο να κατανοήσει το φυσικό κόσμο, και η μηχανική των
διαφόρων τομέων δεν έχει αυτόν το σκοπό. Εξαίρεση αποτελεί η λεγόμενη
“επιστήμη υπολογιστών” (που είναι ουσιαστικά μια μηχανική αλλά με
λογισμικό, όχι με υλικό μέσο), γιατί η γνώση της χρήσης υπολογιστών
επιτρέπει την εκτέλεση “πειραμάτων” (εικονικών έστω) μέσω των οποίων
είτε επαληθεύονται είτε
απορρίπτονται επιστημονικές υποθέσεις. Εντούτοις, μπορεί σαν μηχανικός
να είστε σε θέση να διδάξετε επιστήμες που βρίσκονται στο υπόβαθρο των
γνώσεών σας — π.χ., φυσική, χημεία, μαθηματικά, κλπ. Επικοινωνείστε στο
dep.science@gmail.com για περαιτέρω
συνεννόηση.
![]() Οποιοσδήποτε μη επιστημονικός τομέας· για το ποιοι τομείς
γνώσης είναι επιστημονικοί ή μη, δείτε το μάθημα «Επιστημονική Μέθοδος &
Παραδοχές» (Ε1).
Οποιοσδήποτε μη επιστημονικός τομέας· για το ποιοι τομείς
γνώσης είναι επιστημονικοί ή μη, δείτε το μάθημα «Επιστημονική Μέθοδος &
Παραδοχές» (Ε1).
Περιοχές έρευνας στο Δ.Ε.Π.
Το Δ.Ε.Π. δεν υπάρχει μόνο για να “μεταλαμπαδεύει” τη γνώση, αλλά φιλοδοξεί να την παράγει κιόλας, μέσω έρευνας. Το σε ποια πεδία της επιστήμης γίνεται έρευνα εξαρτάται βέβαια από τα ερευνητικά ενδιαφέροντα των εκάστοτε διδασκόντων. Σύμφωνα πάντα με τη φιλοσοφία του Δ.Ε.Π., ως ερευνητής δεν επιζητείτε το οικονομικό όφελος, αλλά την ικανοποίηση των ερευνητικών αναζητήσεών σας — με άλλα λόγια, η έρευνα στο Δ.Ε.Π. είναι αυτοσκοπός. Βεβαίως, κανείς δεν σας εμποδίζει να προχωρήσετε σε δημοσιεύσεις εφόσον παραγάγετε αποτελέσματα (αντίθετα, ενθαρρύνεστε να δημοσιεύετε τα αποτελέσματά σας)· οπότε μέσω των δημοσιεύσεων είναι δυνατό να υπάρξει και όφελος οικονομικής φύσης, έμμεσα φυσικά. Το Δ.Ε.Π., σαν διαδικτυακή οντότητα, δεν είναι σε θέση να σας παρέχει εργαστήρια και υλικοτεχνικά μέσα, στα οποία υποτίθεται πως ήδη έχετε πρόσβαση. Αυτό που παρέχει το Δ.Ε.Π. είναι η καθοδήγηση εκ μέρους των διδασκόντων (που ονομάζονται “επιβλέποντες” εδώ, στον ερευνητικό τομέα), μέσω των γνώσεων και της πείρας που διαθέτουν στα πεδία που ανήκουν στα ενδιαφέροντά τους. Προς το παρόν, τα παρακάτω πεδία είναι ανοιχτά σε αναζήτηση ενδιαφερομένων ερευνητών και συν-ερευνητών:
![]() Αυτοματοποίηση εκμάθησης φυσικής γλώσσας. ΥΠ: Γ2, Γ3, Υ2·
ΠΠ: Υ3, Ν2. Περιγραφή:
σκοπός είναι η ανάπτυξη λογισμικού συστήματος που
μαθαίνει πολλαπλά χαρακτηριστικά φυσικών γλωσσών (οποιωνδήποτε,
αλλά κάποιες συγκεκριμένες χρησιμοποιούνται σαν παραδείγματα, π.χ.,
ελληνική, αγγλική) εξετάζοντας μεγάλα γραπτά κείμενα. Τα χαρακτηριστικά
της γλώσσας που μαθαίνονται περιλαμβάνουν τη φωνολογία (φωνοτακτικούς
κανόνες), την ορθογραφία (ορθοτακτικούς κανόνες), τη μορφολογία (ανάλυση,
και σύνδεση
μορφημάτων με νοήματα), και το
συντακτικό (συντακτική ανάλυση, συντακτικούς κανόνες). Απώτερος
στόχος η αυτόματη μετάφραση μεταξύ γλωσσών. Επιθυμητή η γνώση
C++, ή Java.
Αυτοματοποίηση εκμάθησης φυσικής γλώσσας. ΥΠ: Γ2, Γ3, Υ2·
ΠΠ: Υ3, Ν2. Περιγραφή:
σκοπός είναι η ανάπτυξη λογισμικού συστήματος που
μαθαίνει πολλαπλά χαρακτηριστικά φυσικών γλωσσών (οποιωνδήποτε,
αλλά κάποιες συγκεκριμένες χρησιμοποιούνται σαν παραδείγματα, π.χ.,
ελληνική, αγγλική) εξετάζοντας μεγάλα γραπτά κείμενα. Τα χαρακτηριστικά
της γλώσσας που μαθαίνονται περιλαμβάνουν τη φωνολογία (φωνοτακτικούς
κανόνες), την ορθογραφία (ορθοτακτικούς κανόνες), τη μορφολογία (ανάλυση,
και σύνδεση
μορφημάτων με νοήματα), και το
συντακτικό (συντακτική ανάλυση, συντακτικούς κανόνες). Απώτερος
στόχος η αυτόματη μετάφραση μεταξύ γλωσσών. Επιθυμητή η γνώση
C++, ή Java.
![]() Επεξεργασία και “κατανόηση” διδιάστατης εικόνας λίγων χρωμάτων. ΥΠ: Υ3,
Ν2. Περιγραφή:
σκοπός είναι η ανάπτυξη λογισμικού συστήματος που
επεξεργάζεται εικόνα “λίγων χρωμάτων” (δηλαδή όχι φωτογραφία αλλά εικόνα
με λίγες και ομοιόμορφα χρωματισμένες περιοχές),
και παράγει μια εσωτερική παράσταση που αντιστοιχεί στην “κατανόηση” της
εικόνας. Το σύστημα μπορεί να αποθηκεύσει την κατανόηση, να την
ανακαλέσει αργότερα, και να παραγάγει μια άλλη εικόνα χρησιμοποιώντας την
κατανόηση — εικόνα που βέβαια είναι μόνο περίπου ίδια με την
αρχική. Στόχος είναι η προσεγγιστική κατανόηση και δυνατότητα
αποθήκευσης & ανάκλησης βάσει περιεχομένου τέτοιων εικόνων (που συνήθως
απαντώνται σαν gifs). Απώτερος στόχος: επέκταση
της λειτουργίας αυτής σε κανονικές φωτογραφίες. Επιθυμητή η γνώση
C++, ή Java.
Επεξεργασία και “κατανόηση” διδιάστατης εικόνας λίγων χρωμάτων. ΥΠ: Υ3,
Ν2. Περιγραφή:
σκοπός είναι η ανάπτυξη λογισμικού συστήματος που
επεξεργάζεται εικόνα “λίγων χρωμάτων” (δηλαδή όχι φωτογραφία αλλά εικόνα
με λίγες και ομοιόμορφα χρωματισμένες περιοχές),
και παράγει μια εσωτερική παράσταση που αντιστοιχεί στην “κατανόηση” της
εικόνας. Το σύστημα μπορεί να αποθηκεύσει την κατανόηση, να την
ανακαλέσει αργότερα, και να παραγάγει μια άλλη εικόνα χρησιμοποιώντας την
κατανόηση — εικόνα που βέβαια είναι μόνο περίπου ίδια με την
αρχική. Στόχος είναι η προσεγγιστική κατανόηση και δυνατότητα
αποθήκευσης & ανάκλησης βάσει περιεχομένου τέτοιων εικόνων (που συνήθως
απαντώνται σαν gifs). Απώτερος στόχος: επέκταση
της λειτουργίας αυτής σε κανονικές φωτογραφίες. Επιθυμητή η γνώση
C++, ή Java.
![]() Οπτική αναγνώριση γραμματοσειρών με εκμάθηση. ΥΠ: Υ3. Περιγραφή:
σκοπός είναι η ανάπτυξη λογισμικού συστήματος το οποίο
μαθαίνει να αναγνωρίζει οπτικά γραμματοσειρές οποιασδήποτε αλφαβητικής
γλώσσας. Για κάθε γραμματοσειρά το σύστημα υπόκειται σε ένα αρχικό στάδιο
εκπαίδευσης. Μπορεί να διαβάσει κείμενο σε οποιαδήποτε κλίση
(ακόμα και ανάποδα), αναγνωρίζει την περιεχόμενη γλώσσα (εφόσον έχει ήδη
μάθει αρκετά για τη γλώσσα αυτή), και χρησιμοποιεί τη γνώση των λέξεων
που έχει αποκτήσει προκειμένου να αποσαφηνίσει γράμματα που δεν είναι
τυπωμένα καθαρά. Στόχος είναι η αυτόματη ανάγνωση παλαιών τυπωμένων
ελληνικών κειμένων (περιλαμβανομένου και του πολυτονικού). Επιθυμητή η γνώση C++, ή Java.
Οπτική αναγνώριση γραμματοσειρών με εκμάθηση. ΥΠ: Υ3. Περιγραφή:
σκοπός είναι η ανάπτυξη λογισμικού συστήματος το οποίο
μαθαίνει να αναγνωρίζει οπτικά γραμματοσειρές οποιασδήποτε αλφαβητικής
γλώσσας. Για κάθε γραμματοσειρά το σύστημα υπόκειται σε ένα αρχικό στάδιο
εκπαίδευσης. Μπορεί να διαβάσει κείμενο σε οποιαδήποτε κλίση
(ακόμα και ανάποδα), αναγνωρίζει την περιεχόμενη γλώσσα (εφόσον έχει ήδη
μάθει αρκετά για τη γλώσσα αυτή), και χρησιμοποιεί τη γνώση των λέξεων
που έχει αποκτήσει προκειμένου να αποσαφηνίσει γράμματα που δεν είναι
τυπωμένα καθαρά. Στόχος είναι η αυτόματη ανάγνωση παλαιών τυπωμένων
ελληνικών κειμένων (περιλαμβανομένου και του πολυτονικού). Επιθυμητή η γνώση C++, ή Java.
Οι ενδιαφερόμενοι ερευνητές παρακαλούνται να επικοινωνήσουν στο dep.science@gmail.com για περισσότερες πληροφορίες.
Αν θέλετε να λειτουργήσετε ως επιβλέπων που έχει να προτείνει άλλα ερευνητικά θέματα, παρακαλούμε επικοινωνήστε επίσης στην ανωτέρω διεύθυνση, σημειώνοντας όμως πως θα πρέπει να λειτουργείτε και ως εν δυνάμει διδάσκων σε τουλάχιστον ένα μάθημα του Δ.Ε.Π., είτε κάποιου από αυτά που ήδη προσφέρονται, είτε άλλου που θα προτείνετε εσείς (με αναλυτική περιγραφή περιεχομένων).
Περιεχόμενα μαθημάτων, αναλυτικά
Σημείωση: με κλικ όπου υπάρχει σύνδεσμος στον τίτλο
με το εικονίδιο
![]() μεταφέρεστε στις
αναλυτικές σημειώσεις του μαθήματος.
μεταφέρεστε στις
αναλυτικές σημειώσεις του μαθήματος.
Α1. Πλανήτες – Πλανητικά
Συστήματα: Δημιουργία και εξέλιξη πλανητικών συστημάτων — Τί είναι
πλανήτης και σε τί διαφέρει από έναν αστέρα — Νόμοι
του Kepler — Οι τέσσερις “γήινοι” πλανήτες — Δημιουργία Σελήνης —
Ιδιαιτερότητα της Σελήνης για τη βιόσφαιρα της Γης — Οι τέσσερις
“γίγαντες” πλανήτες — Η σημασία των Δία & Κρόνου για τη βιόσφαιρα της
Γης — Το μέλλον του Ήλιου, της Γης, και του ηλιακού συστήματος —
Αστεροειδείς — Μετέωρα, βροχές διαττόντων, και μετεωρίτες — Σώματα σε
τροχιά μετά τον Ποσειδώνα – πλανητοειδή –
πλουτοειδή — Κομήτες και το νέφος του Oort — Απόσταση του
κοντινότερου αστέρα — Πλανήτες εκτός ηλιακού συστήματος.
Α2.
Αστέρες – Αστρικά Συστήματα:
![]()
![]() (κλικ εδώ για αναλυτικές σημειώσεις): Τί είναι ένας
αστέρας — Δημιουργία αστέρων – εξέλιξη – θάνατος — Σχέση θερμοκρασίας –
χρώματος — Μεγέθη αστέρων και κατανομή μεγεθών — Τυπικές αποστάσεις
μεταξύ αστέρων — Αστέρες της γειτονιάς του Ήλιου — Πολλαπλά συστήματα —
Ανοιχτά σμήνη — Σφαιρωτά σμήνη — Πλανητικά νεφελώματα — Αστέρες
νετρονίων — Υπερκαινοφανείς — Μαύρες τρύπες — Νεφελώματα — Θέση του
Ήλιου στο Γαλαξία — Τί είναι ο γαλαξίας — Είδη γαλαξιών — Γειτονικοί
γαλαξίες — Δομή του παρατηρήσιμου τμήματος του σύμπαντος.
(κλικ εδώ για αναλυτικές σημειώσεις): Τί είναι ένας
αστέρας — Δημιουργία αστέρων – εξέλιξη – θάνατος — Σχέση θερμοκρασίας –
χρώματος — Μεγέθη αστέρων και κατανομή μεγεθών — Τυπικές αποστάσεις
μεταξύ αστέρων — Αστέρες της γειτονιάς του Ήλιου — Πολλαπλά συστήματα —
Ανοιχτά σμήνη — Σφαιρωτά σμήνη — Πλανητικά νεφελώματα — Αστέρες
νετρονίων — Υπερκαινοφανείς — Μαύρες τρύπες — Νεφελώματα — Θέση του
Ήλιου στο Γαλαξία — Τί είναι ο γαλαξίας — Είδη γαλαξιών — Γειτονικοί
γαλαξίες — Δομή του παρατηρήσιμου τμήματος του σύμπαντος.
Βιολογία: Η βιολογία στο Δ.Ε.Π. ελάχιστη σχέση έχει με το βαρετό μάθημα που συναντά κανείς στο Γυμνάσιο–Λύκειο. Πρόκειται για έναν ζωντανό τομέα της επιστήμης, παρόλο που ασχολείται και με πράγματα που συνέβησαν εκατομμύρια χρόνια πριν. Είναι αδύνατο να κατανοήσουμε σε βάθος το γιατί οι ζωντανοί οργανισμοί παρουσιάζονται με τη μορφή που έχουν σήμερα αν δεν εξετάσουμε το με τί έμοιαζαν στο μακρυνό παρελθόν. Πέρα όμως από τη γνώση περί ζωντανών οργανισμών, μέσω της βιολογίας μπορούμε να απαντήσουμε έναν αριθμό ερωτημάτων που σπάνια τα σκεφτόμαστε σαν ερωτήματα, και που αφορούν εμάς τους ανθρώπους. Παραδείγματος χάρη: Γιατί γερνάμε και πεθαίνουμε; Γιατί απ’ όλα τα πλάσματα μόνο τα μωρά των ανθρώπων γεννιούνται αβοήθητα, ανίκανα ακόμη και να γυρίσουν στο πλάι ή να σηκώσουν το κεφάλι, και παραμένουν ανίκανα να περπατήσουν για ένα χρόνο περίπου; Γιατί μόνο οι άνθρωποι (οι γυναίκες) πονούν κατά τον τοκετό; Γιατί είμαστε “γυμνοί”, χωρίς τρίχες στο σώμα, αντίθετα με σχεδόν όλα τα άλλα θηλαστικά; Γιατί οι γυναίκες έχουν τόσο μεγάλο στήθος ακόμα και όταν δεν θηλάζουν (και πάλι, αντίθετα με σχεδόν όλα τα άλλα θηλαστικά); Γιατί μας αρέσουν τα γλυκά και απεχθανόμαστε τα πικρά; Πότε και σε ποιο σημείο του πλανήτη πρωτοεμφανίστηκε το ανθρώπινο είδος, και με τί μοιάζαμε τότε; Γιατί υπάρχουν φυλές, όπως η μαύρη, η λευκή, κλπ; Γιατί κάποιες κοινωνίες (οι “Δυτικές”) προόδευσαν τόσο πολύ τεχνολογικά και κυριάρχησαν πάνω σε όλες τις υπόλοιπες; Όλα αυτά, όπως και μια πληθώρα άλλων ερωτημάτων, δεν αντιμετωπίζονται στη βιολογία του Γυμνασίου–Λυκείου γιατί εκεί εξετάζεται επιφανειακά μόνο το τώρα, ενώ στα σχετικά μαθήματα του Δ.Ε.Π. μαθαίνει κανείς για το τότε και το τώρα σαν μια ολότητα, που έτσι γίνεται επιδεκτική νοήματος.
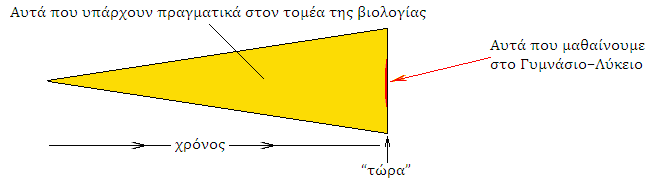
Το παραπάνω διάγραμμα επιχειρεί να εξηγήσει σχηματικά τη διαφορά μεταξύ γυμνασιακής βιολογίας και βιολογίας όπως αντιμετωπίζεται στο Δ.Ε.Π.
Β1.
Παλαιοντολογία
![]()
![]() (κλικ εδώ για αναλυτικές σημειώσεις):
Στόχος, εύρος, και προαπαιτούμενα του μαθήματος — Η απίστευτα
μεγάλη ιστορία της ζωής στη Γη — Γεωλογική διαίρεση του χρόνου σε
Μεγααιώνες — Πριν από τη ζωή: Αδαίος ή Καταρχαιοζωικός Μεγααιώνας –
Δημιουργία Γης και Σελήνης – συνθήκες για εμφάνιση ζωής – τεκτονικές
πλάκες και σημασία της τεκτονικής δραστηριότητας για τη βιόσφαιρα
— Αρχαιοζωικός Μεγααιώνας – διαίρεση σε Αιώνες – σχηματισμός ηπείρων,
μορφολογία ωκεανών και ξηράς ανά τους αιώνες – τί είναι ζωή – γήινη ή
εξωγήινη προέλευση – η αυγή της ζωής – τα πιο αρχαία απομεινάρια ζωής
στη Γη· στρωματόλιθοι – γενικές ιδιότητες και δομή βακτηρίων — Πώς προσδιορίζουμε ηλικίες – πετρώματα και απολιθώματα, πώς
βρίσκεται η ηλικία-τους — Κυανοβακτήρια και η οικοδόμηση του οξυγόνου —
Προτεροζωικός Μεγααιώνας — Εμφάνιση ευκαρυωτικών
κυττάρων – συνθήκες — Συμβίωση και ενδοσυμβίωση — “Ανακάλυψη” του σεξ —
Πολυκύτταροι οργανισμοί — Ζώα Εδιακαρανικής περιόδου — Εξέλιξη των
σκελετών — Η “έκρηξη” της Κάμβριας περιόδου — Αρθρόποδα — Τα πρώτα
σπονδυλωτά — Κατάκτηση της ξηράς από τα πρώτα τετράποδα ψάρια — Πρώτα
αμφίβια — Ερπετά — Δεινόσαυροι — Εξέλιξη της πτητικής ικανότητας και
πρώτα πτηνά — Προέλευση των θηλαστικών — Εξέλιξη φυτών — Γιατί τα
λουλούδια είναι όμορφα — Εξαφάνιση δεινοσαύρων — Καινοζωικός αιώνας και
θηλαστικά — Μαρσιποφόρα, διαχωρισμός Αυστραλίας από Ανταρκτική, και
ένωση των δύο Αμερικών — Εξέλιξη πρωτευόντων — Πρώτα ανθρωποειδή —
Εμφάνιση του γένους Homo — Νεάντερταλ, Κρο Μανιόν, και η
νεότερη εποχή των παγετώνων.
(κλικ εδώ για αναλυτικές σημειώσεις):
Στόχος, εύρος, και προαπαιτούμενα του μαθήματος — Η απίστευτα
μεγάλη ιστορία της ζωής στη Γη — Γεωλογική διαίρεση του χρόνου σε
Μεγααιώνες — Πριν από τη ζωή: Αδαίος ή Καταρχαιοζωικός Μεγααιώνας –
Δημιουργία Γης και Σελήνης – συνθήκες για εμφάνιση ζωής – τεκτονικές
πλάκες και σημασία της τεκτονικής δραστηριότητας για τη βιόσφαιρα
— Αρχαιοζωικός Μεγααιώνας – διαίρεση σε Αιώνες – σχηματισμός ηπείρων,
μορφολογία ωκεανών και ξηράς ανά τους αιώνες – τί είναι ζωή – γήινη ή
εξωγήινη προέλευση – η αυγή της ζωής – τα πιο αρχαία απομεινάρια ζωής
στη Γη· στρωματόλιθοι – γενικές ιδιότητες και δομή βακτηρίων — Πώς προσδιορίζουμε ηλικίες – πετρώματα και απολιθώματα, πώς
βρίσκεται η ηλικία-τους — Κυανοβακτήρια και η οικοδόμηση του οξυγόνου —
Προτεροζωικός Μεγααιώνας — Εμφάνιση ευκαρυωτικών
κυττάρων – συνθήκες — Συμβίωση και ενδοσυμβίωση — “Ανακάλυψη” του σεξ —
Πολυκύτταροι οργανισμοί — Ζώα Εδιακαρανικής περιόδου — Εξέλιξη των
σκελετών — Η “έκρηξη” της Κάμβριας περιόδου — Αρθρόποδα — Τα πρώτα
σπονδυλωτά — Κατάκτηση της ξηράς από τα πρώτα τετράποδα ψάρια — Πρώτα
αμφίβια — Ερπετά — Δεινόσαυροι — Εξέλιξη της πτητικής ικανότητας και
πρώτα πτηνά — Προέλευση των θηλαστικών — Εξέλιξη φυτών — Γιατί τα
λουλούδια είναι όμορφα — Εξαφάνιση δεινοσαύρων — Καινοζωικός αιώνας και
θηλαστικά — Μαρσιποφόρα, διαχωρισμός Αυστραλίας από Ανταρκτική, και
ένωση των δύο Αμερικών — Εξέλιξη πρωτευόντων — Πρώτα ανθρωποειδή —
Εμφάνιση του γένους Homo — Νεάντερταλ, Κρο Μανιόν, και η
νεότερη εποχή των παγετώνων.
Β2. Ταξινόμηση Ειδών: Γιατί γίνεται η ταξινόμηση των ειδών — Διαφορά ταξινομικού και φυλογενετικού δέντρου — Κατηγορίες ταξινόμησης — Τα πέντε βασίλεια — Βακτήρια και Αρχαιοβακτήρια — Πρώτιστα – αμοιβάδες, διάτομα — Μύκητες και παρασιτισμός — Φυτά και η εξέλιξή τους — Φύλα ζώων — Σπόγγοι — Κνιδάρια – κοράλλια, μέδουσες — Κτενοφόρα — Πλατυέλμινθες — Νηματώδη — Γεωσκώληκες — Μαλάκια — Αρθρόποδα – οστρακόδερμα, σκορπιοί, αράχνες, έντομα — Εχινοδέρματα – αχινοί, αστερίες — Χορδωτά – κεφαλοχορδωτά, ουροχορδωτά, και σπονδυλωτά — Άγναθα και γναθοστόματα — Χονδρίχθυες – καρχαρίες, σαλάχια, χίμαιρες — Οστεΐχθυες – λοβοπτερυγωτά και ακτινοπτερυγωτά ψάρια — Αμφίβια — Ερπετά – κροκοδείλια, χελώνες, σαύρες & φίδια, σφηνόδων — Πτηνά – ανασκόπηση διαφόρων τάξεων — Θηλαστικά – μονοτρήματα, μαρσιποφόρα, ευθήρια — Ανασκόπηση διαφόρων τάξεων θηλαστικών με πλακούντα — Πρωτεύοντα – κερκοπίθηκοι – πίθηκοι Νέου Κόσμου – ανθρωπίδαι – ανθρωπίναι – Γενικά χαρακτηριστικά του ταξινομικού δέντρου: γιατί είναι έτσι; είναι αυθαίρετο ή επιβάλλεται από τη φύση;
Β3. Κύτταρο – Γονίδια: Κυτταρικές μεμβράνες – διαπερατότητα, ώσμωση — Προκαρυωτικά και ευκαρυωρικά κύτταρα – διαφορές — Πυρήνας – DNA — Ριβοσώματα — Ενδοπλασμικό δίκτυο — Μηχανές Γκόλτζι — Λυσοσώματα — Μιτοχόνδρια – ATP — Κυτταροσκελετός — Αντιδράσεις οξειδοαναγωγής — Φωτοσύνθεση – χλωροπλάστες — Γλυκόλυση — Αναπνοή — Δομή του DNA — Αναπαραγωγή (αντιγραφή) του DNA – μεταλλάξεις, επιδιορθώσεις — Z-DNA και B-DNA — Δομή ευκαρυωτικών χρωμοσωμάτων — Οργάνωση του γονιδιώματος — RNA — Ο γενετικός κώδικας – σύνθεση πρωτεϊνών, αγγελιοφόρο RNA — Ο κυτταρικός κύκλος – μίτωση, κυτταροκίνηση, μείωση — Γενετική του Mendel — Φαινοτυπική έκφραση των μεταλλάξεων — Καθορισμός φύλου.
Β4. Εξέλιξη Ειδών: Πώς συντελείται η εξέλιξη – τα θεμελιώδη αξιώματα — Προδαρβινική εξελικτική σκέψη – Αναξαγόρας, Γένεσις 1, Lamarck — Πρώτη διατύπωση από Darwin, 1859, και Wallace — Μετέπειτα λανθασμένες παραδοχές – “έμφυτη τάση” ειδών προς σταδιακή και συνεχή εξέλιξη — Νεότερες παραδοχές – “διακοπτόμενη ισορροπία” — Η έννοια της “εσοχής” (niche) και της περιβαλλοντικής πίεσης — Συμβίωση – μιτοχόνδρια και ευκαρυωτικά κύτταρα – εντερικά βακτήρια — Η έννοια της “προσαρμοστικής διασποράς” (adaptive radiation) — Το “εγωιστικό γονίδιο” του Dawkins και η εξήγηση της αλληλοβοήθειας και της αυτοθυσίας (αλτρουϊσμού) — Τί είναι αυτό που εξελίσσεται, το είδος ή το γονίδιο; — Η “μάχη” μεταξύ μαρσιποφόρων και θηλαστικών με πλακούντα — Μικροπεριβάλλοντα και η έννοια του “όσο πιο μεγάλο τόσο πιο ευάλωτο” — Όργανα που είναι εξελικτικά κατάλοιπα — Είδη-“απομεινάρια” της εξελικτικής διαδικασίας — Οντογένεση και συμπεράσματα από τη μελέτη-της — Εξέλιξη του ανθρώπου (περιληπτικά) — Τί είναι ο “δημιουργισμός” (creationism) — Εξήγηση άλλων αναπάντητων ερωτημάτων μέσω της εξέλιξης.
Β5. Εξέλιξη Ανθρώπου & Κοινωνιών: Ιστορικές απόψεις — Πώς γίνεται η χρονολόγηση των απολιθωμάτων — Η σχέση Ανθρώπου–Χιμπαντζή και το “μοριακό ρολόι” του DNA — Προγονικά είδη πιθήκων — Ανθρωπίναι — Απαρχή όρθιας στάσης — Αυστραλοπίθηκοι – “Lucy” — Άνθρωπος ο Όρθιος – πρώτη έξοδος από την Αφρική — Η επιστήμη της ταφής — Τεχνολογία εργαλείων — Οι Νεάντερταλ — Άνθρωπος ο Σοφός – προέλευση — Γιατί έχουμε μαλλιά στο κεφάλι αλλά όχι στο σώμα, και άλλα ερωτήματα που αφορούν τον άνθρωπο — Δεύτερη ή τρίτη έξοδος από την Αφρική — Το “Μεγάλο Βήμα Εμπρός” – γλώσσα, τέχνη, εργαλεία — Πώς δημιουργήθηκαν οι φυλές – Νέγροι, Ασιάτες Άπω Ανατολής, Αυστραλοί Αβορίγινες, Ινδιάνοι, Καυκάσιοι — Κυνηγοί–Συλλέκτες — Αγροκαλλιέργεια – γιατί αναπτύχθηκε σε ορισμένους τόπους — Συνέπειες αγροτικής ζωής – προέλευση κοινωνικών τάξεων — Εξόρυξη μετάλλων – τεχνολογία — Γιατί έγινε η παγκόσμια εξάπλωση και κυριαρχία των Ευρωπαϊκών κοινωνιών — “Πρόοδος” = διαρκής πάλη του ανθρώπου ενάντια στο 2ο νόμο της θερμοδυναμικής.
Γλωσσολογία: Γλωσσολογία είναι η επιστήμη που ασχολείται με τη
γλώσσα· όχι όμως με μία συγκεκριμένη, αλλά με την
ανθρώπινη γλώσσα στη γενικότητά της. Έτσι, μέσω της γλωσσολογίας
μαθαίνει κανείς για ιδιότητες που έχουν όλες οι γλώσσες του
κόσμου, ή κάποιες γλώσσες, κλπ. Εδώ θα μάθετε ποιοι είναι οι ήχοι
(φωνήεντα και σύμφωνα) που μπορούν να παράγουν όλοι οι άνθρωποι στην
οικουμένη· ακόμα και το ποιοι είναι οι ήχοι της νέας ελληνικής, πράγμα
που σχεδόν όλοι οι γηγενείς ομιλητές της ελληνικής αγνοούν· ποιες είναι
οι μορφολογικές δομές και ποιες οι συντακτικές δομές της γλώσσας· και
άλλα πολλά. Αν είστε
φιλόλογος, θα μάθετε πράγματα (ιδίως στο μάθημα Γ1) που θα σας δώσουν
μια τελείως διαφορετική οπτική για το αντικείμενό σας· θα δείτε την
ελληνική (αλλά και κάθε άλλη γλώσσα) “με άλλο μάτι”.
Γ1. Θεμελιώδεις Αρχές Γλωσσολογίας
![]()
![]() (κλικ εδώ για αναλυτικές σημειώσεις): Τί
το ιδιαίτερο έχει η ανθρώπινη ομιλία σε σχέση με την επικοινωνία των
ζώων — Τί είναι γλώσσα – η σύγχυση της γλώσσας με τη γραφή — Γλώσσα
είναι αυτό που ομιλείται από τους “γηγενείς ομιλητές”
– υπεροχή της περιγραφής έναντι
της συνταγής στη γλώσσα – καθαρεύουσα έναντι δημοτικής – γιατί τα Ρουμελιώτικα (π.χ.) είναι τόσο
σωστά όσο και τα “Αθηναϊκά” ελληνικά – δεν υπάρχει “λάθος γλώσσα”
μιας ολόκληρης ομάδας γηγενών ομιλητών — Διαφορά γηγενούς από μη γηγενή
ομιλητή – Η υπόθεση του έμφυτου της
γλώσσας – γενική (ή καθολική) γλώσσα, και η θεωρία
παραμέτρων του Τσόμσκι – κρίσιμη
περίοδος ή “παράθυρο” απόκτησης γλώσσας – πίτζιν και κρεολές γλώσσες – οπτικές γλώσσες — Δομή της γλώσσας –
φωνητική, φωνολογία, μορφολογία, συντακτικό, σημαντικό,
πραγματικό — Οι γλώσσες εξελίσσονται – σύντομη
ανασκόπηση της εξέλιξης της ελληνικής – προέλευση της
ελληνικής — Διάλεκτος,
ιδίωμα,
ιδιόλεκτος, κοινόλεκτος – πότε μιλάμε για διαφορετικές διαλέκτους και πότε για
διαφορετικές γλώσσες – ο ρόλος της πολιτικής
στον ορισμό γλώσσας και διαλέκτου
—
Σχέση
γλώσσας και νόησης – υποσυνείδητο και συνειδητό – οι γλωσσικοί
νόμοι είναι (συνήθως) υπεράνω της βούλησης των ανθρώπων.
(κλικ εδώ για αναλυτικές σημειώσεις): Τί
το ιδιαίτερο έχει η ανθρώπινη ομιλία σε σχέση με την επικοινωνία των
ζώων — Τί είναι γλώσσα – η σύγχυση της γλώσσας με τη γραφή — Γλώσσα
είναι αυτό που ομιλείται από τους “γηγενείς ομιλητές”
– υπεροχή της περιγραφής έναντι
της συνταγής στη γλώσσα – καθαρεύουσα έναντι δημοτικής – γιατί τα Ρουμελιώτικα (π.χ.) είναι τόσο
σωστά όσο και τα “Αθηναϊκά” ελληνικά – δεν υπάρχει “λάθος γλώσσα”
μιας ολόκληρης ομάδας γηγενών ομιλητών — Διαφορά γηγενούς από μη γηγενή
ομιλητή – Η υπόθεση του έμφυτου της
γλώσσας – γενική (ή καθολική) γλώσσα, και η θεωρία
παραμέτρων του Τσόμσκι – κρίσιμη
περίοδος ή “παράθυρο” απόκτησης γλώσσας – πίτζιν και κρεολές γλώσσες – οπτικές γλώσσες — Δομή της γλώσσας –
φωνητική, φωνολογία, μορφολογία, συντακτικό, σημαντικό,
πραγματικό — Οι γλώσσες εξελίσσονται – σύντομη
ανασκόπηση της εξέλιξης της ελληνικής – προέλευση της
ελληνικής — Διάλεκτος,
ιδίωμα,
ιδιόλεκτος, κοινόλεκτος – πότε μιλάμε για διαφορετικές διαλέκτους και πότε για
διαφορετικές γλώσσες – ο ρόλος της πολιτικής
στον ορισμό γλώσσας και διαλέκτου
—
Σχέση
γλώσσας και νόησης – υποσυνείδητο και συνειδητό – οι γλωσσικοί
νόμοι είναι (συνήθως) υπεράνω της βούλησης των ανθρώπων.
Γ2. Φωνητική – Φωνολογία
![]()
![]() (κλικ εδώ για αναλυτικές σημειώσεις):
Φωνητική — Οι ήχοι της
γλώσσας, και η παράστασή τους με σύμβολα — Φωνήεντα – τα
ελληνικά φωνήεντα “φωνάζουν δυνατά”, αλλά είναι πέντε, όχι “επτά” – ο
“φωνολογικός χώρος” των φωνηέντων όλου του κόσμου — Διάρκεια — Δίφθογγοι
– τί είναι δίφθογγοι (όχι αυτό που μαθαίνουμε στο Δημοτικό), και πού
υπάρχουν στην ελληνική, πού σε άλλες γλώσσες — Σύμφωνα – ο “φωνολογικός
χώρος” των συμφώνων όλου του κόσμου — Τονισμός και τονικότητα – τονικές γλώσσες —
Φωνολογία — Διαφορά φωνητικής από
φωνολογία – παραδείγματα: πάθη συμφώνων στα όρια των λέξεων –
ουρανικοποίηση: τα “αόρατα” ελληνικά σύμφωνα —Αλλόφωνα – ο γηγενής ομιλητής δεν “ακούει” τα αλλόφωνα,
ο μη γηγενής δεν “ακούει” τη διαφορά – ελάχιστα ζεύγη — Τί είναι η
συλλαβή και ποια δομή έχει – η έννοια της
“ηχηρότητας” – πώς δομούνται οι συλλαβές στην ελληνική, και πώς σε
άλλες γλώσσες — Μοτίβα τονισμού ελληνικών και
αγγλικών λέξεων.
(κλικ εδώ για αναλυτικές σημειώσεις):
Φωνητική — Οι ήχοι της
γλώσσας, και η παράστασή τους με σύμβολα — Φωνήεντα – τα
ελληνικά φωνήεντα “φωνάζουν δυνατά”, αλλά είναι πέντε, όχι “επτά” – ο
“φωνολογικός χώρος” των φωνηέντων όλου του κόσμου — Διάρκεια — Δίφθογγοι
– τί είναι δίφθογγοι (όχι αυτό που μαθαίνουμε στο Δημοτικό), και πού
υπάρχουν στην ελληνική, πού σε άλλες γλώσσες — Σύμφωνα – ο “φωνολογικός
χώρος” των συμφώνων όλου του κόσμου — Τονισμός και τονικότητα – τονικές γλώσσες —
Φωνολογία — Διαφορά φωνητικής από
φωνολογία – παραδείγματα: πάθη συμφώνων στα όρια των λέξεων –
ουρανικοποίηση: τα “αόρατα” ελληνικά σύμφωνα —Αλλόφωνα – ο γηγενής ομιλητής δεν “ακούει” τα αλλόφωνα,
ο μη γηγενής δεν “ακούει” τη διαφορά – ελάχιστα ζεύγη — Τί είναι η
συλλαβή και ποια δομή έχει – η έννοια της
“ηχηρότητας” – πώς δομούνται οι συλλαβές στην ελληνική, και πώς σε
άλλες γλώσσες — Μοτίβα τονισμού ελληνικών και
αγγλικών λέξεων.
Γ3. Μορφολογία – Τί είναι τα μορφήματα — Κατηγορίες – ελεύθερα και δεσμευμένα – λεξικά και γραμματικά – δεσμευμένα παραγωγικά και δεσμευμένα κλιτικά — Αλλόμορφα — Η ιεραρχική δομή των λέξεων — Διαδικασίες σύνθεσης λέξεων — Μορφολογική ανάλυση — Μορφολογικοί τύποι γλωσσών – αναλυτικές, συνθετικές, πολυσυνθετικές, κλπ. —
Γ4.
Συντακτικό
![]()
![]() (κλικ εδώ για αναλυτικές σημειώσεις):
Παραγωγικότητα λέξεων και προτάσεων – Γραμμικότητα – Ιεραρχική δόμηση
– Κριτήρια συστατικότητας – Ιδιότητες συστατικών — Αμφισημία —
Λεκτικές κατηγορίες και υποκατηγορίες – ουσιαστικά – ρήματα –
επίθετα – επιρρήματα – νοηματικές και λειτουργικές
λέξεις — Σχέση μεταξύ μορφολογίας και συντακτικού — Φραστικές κατηγορίες — Δενδροειδή διαγράμματα — Κανόνες
φραστικής δόμησης — Αναδρομή — Μετασχηματισμοί — Θεωρία X-bar.
(κλικ εδώ για αναλυτικές σημειώσεις):
Παραγωγικότητα λέξεων και προτάσεων – Γραμμικότητα – Ιεραρχική δόμηση
– Κριτήρια συστατικότητας – Ιδιότητες συστατικών — Αμφισημία —
Λεκτικές κατηγορίες και υποκατηγορίες – ουσιαστικά – ρήματα –
επίθετα – επιρρήματα – νοηματικές και λειτουργικές
λέξεις — Σχέση μεταξύ μορφολογίας και συντακτικού — Φραστικές κατηγορίες — Δενδροειδή διαγράμματα — Κανόνες
φραστικής δόμησης — Αναδρομή — Μετασχηματισμοί — Θεωρία X-bar.
Γ5. Σημασιολογικό &
Πραγματολογικό: Σημασιολογική ανάλυση — Θεωρίες νοήματος — Νόημα
απομονωμένων λέξεων και νόημα συνδυασμών λέξεων. Πραγματολογική ανάλυση.
Γ6. Εξέλιξη Γλωσσών: Γιατί εξελίσσονται οι
γλώσσες — Πώς εξελίσσονται οι γλώσσες – φωνητικά, φωνολογικά,
μορφολογικά, γραμματικά, συντακτικά, σημαντικά — Ποιοι είναι οι
“δράστες” της εξέλιξης — Δάνεια και γεωγραφική συγγένεια — Η συγκριτική
μέθοδος — Το δέντρο της εξέλιξης — Οι κυριώτερες υπεροικογένειες γλωσσών
– ινδοευρωπαϊκή, ουραλική, αλταϊκή, αφροασιατική, αμερινδιανική,
αυστραλοαβοριγινή, καυκασιανή, δραβιδική, νιγηρο–κορδοφανιανή,
σινοθιβετιανή, κ.ά. — Οι ινδοευρωπαϊκές οικογένειες – ελληνική, λατινική,
κελτική, γερμανική, βαλτο-σλαβική, αρμενική, ινδο-ιρανική, χιτιτική,
τοχαρική — Μη ινδοευρωπαϊκές γλώσσες της Ευρώπης.
Γ7. Εφαρμογή: Ιδιότητες της Αρχαίας Ελληνικής: Ενδείξεις (παρατηρήσεις) για την εξέλιξη της ελληνικής γλώσσας — Ο κανόνας των αλφαβήτων — Η δασεία και τα δασέα γράμματα — Ο τονισμός και ενδείξεις για τονική γλώσσα – οξεία, βαρεία, περισπωμένη — Εξέταση ενδείξεων για τα σύμφωνα, ένα προς ένα — Εξέταση ενδείξεων για τα φωνήεντα, ένα προς ένα – ανασκόπηση φωνολογικού χώρου φωνηέντων — Οι δίφθογγοι της αρχαίας ελληνικής — Ανασκόπηση μορφολογίας — Ανασκόπηση συντακτικού — Αλλαγές στο νόημα και στο γένος των λέξεων — Μοτίβα εξέλιξης προς τη νέα ελληνική διαμέσου των αιώνων.
Γ8. Εφαρμογή: Ιδιότητες της Αγγλικής Γλώσσας: Το μάθημα εξετάζει γλωσσολογικές ιδιότητες της αγγλικής γλώσσας άγνωστες στην πλειοψηφία των καθηγητών που διδάσκουν τη γλώσσα αυτή (είτε Ελλήνων, είτε γηγενών ομιλητών της αγγλικής). Το μάθημα απευθύνεται κυρίως στους καθηγητές της αγγλικής, αλλά και σε όσους επιθυμούν μια βαθύτερη γνώση κάποιων ιδιοτήτων αυτής της γλώσσας.
Ε1. Επιστημονική Μέθοδος & Παραδοχές
![]()
![]() (κλικ εδώ για αναλυτικές σημειώσεις) (σύντομο
μάθημα, προαπαιτούμενο όλων): Με τί ασχολείται η επιστήμη —
Επιστημονική μέθοδος – παρατήρηση, πείραμα, συλλογή δεδομένων, θεωρία,
δημοσίευση, κριτική — Τί αποτελεί παρατήρηση & δεδομένο — Επαληθευσιμότητα από
ανεξάρτητο & αντικειμενικό παρατηρητή — Πλήθος παρατηρητών — Θεωρίες – προβλέψεις, διαψευσιμότητα – κύρος
παρατηρητών – ad hominem
επιθέσεις —
Έλεγχος ισχυρισμών μέσω αναφοράς σε πηγές —
Γιατί ο επιστήμονας είναι σκεπτικιστής — Η
θεμελιώδης παραδοχή: “Οτιδήποτε επιδρά στο φυσικό
κόσμο υπόκειται σε επιστημονική έρευνα” —
Επιστημονική “πίστη”
στη λιτότητα της φύσης – ξυράφι του Ockham
– πού οφείλεται —
Επιστημονική “πίστη” στην
κατανοησιμότητα της φύσης — Ασκήσεις –
παρατηρήσεις εξωγήινων, παρατηρήσεις θαυμάτων, παρατηρήσεις οραμάτων,
παρατηρήσεις πρόσκρουσης κομήτη στο Δία, θεωρία της εξέλιξης.
(κλικ εδώ για αναλυτικές σημειώσεις) (σύντομο
μάθημα, προαπαιτούμενο όλων): Με τί ασχολείται η επιστήμη —
Επιστημονική μέθοδος – παρατήρηση, πείραμα, συλλογή δεδομένων, θεωρία,
δημοσίευση, κριτική — Τί αποτελεί παρατήρηση & δεδομένο — Επαληθευσιμότητα από
ανεξάρτητο & αντικειμενικό παρατηρητή — Πλήθος παρατηρητών — Θεωρίες – προβλέψεις, διαψευσιμότητα – κύρος
παρατηρητών – ad hominem
επιθέσεις —
Έλεγχος ισχυρισμών μέσω αναφοράς σε πηγές —
Γιατί ο επιστήμονας είναι σκεπτικιστής — Η
θεμελιώδης παραδοχή: “Οτιδήποτε επιδρά στο φυσικό
κόσμο υπόκειται σε επιστημονική έρευνα” —
Επιστημονική “πίστη”
στη λιτότητα της φύσης – ξυράφι του Ockham
– πού οφείλεται —
Επιστημονική “πίστη” στην
κατανοησιμότητα της φύσης — Ασκήσεις –
παρατηρήσεις εξωγήινων, παρατηρήσεις θαυμάτων, παρατηρήσεις οραμάτων,
παρατηρήσεις πρόσκρουσης κομήτη στο Δία, θεωρία της εξέλιξης.
Ε2.
Ιστορία & Εξέλιξη
της Επιστήμης ![]()
![]() (κλικ εδώ για αναλυτικές σημειώσεις): Προεπιστήμονες (“φυσικοί φιλόσοφοι”) της αρχαίας
Ελλάδας – ποια η διαφορά με
όλη την προηγούμενη αρχαία σκέψη – Θαλής, Αναξίμανδρος, Αναξιμένης, Πυθαγόρας, Ηράκλειτος,
Εμπεδοκλής, Δημόκριτος,
Πλάτων, Αριστοτέλης, Αρίσταρχος ο
Σάμιος — Αρχαίοι Έλληνες
μαθηματικοί και εφευρέτες – Αρχιμήδης,
Ερατοσθένης — Σημασία της Ευκλείδειας γεωμετρίας
στο συνολικό οικοδόμημα της επιστήμης — Αλχημιστές του Μεσαίωνα –
πού έκαναν λάθος — Κοπέρνικος – ηλιοκεντρικό αντί γεωκεντρικό σύστημα,
ξυράφι του Ockham — Η αυγή της επιστημονικής σκέψης – Γαλιλαίος —
René Descartes – Καρτεσιανές συντεταγμένες — Αρχή μαθηματικής ανάλυσης –
Newton, Leibniz — Κλασική φυσική – Newton — Μικροσκόπιο – van Leeuwenhoek, Hooke — Νεότερη ατομική θεωρία – Dalton —
Πρόοδος μαθηματικών και μη
ευκλείδειες γεωμετρίες – Gauss — Ηλεκτρομαγνητική θεωρία – Faraday,
Maxwell — Θεωρία της εξέλιξης των ειδών – Darwin, Wallace — Περιοδικός πίνακας – Mendeleev —
Ανακάλυψη ακτίνων Χ – Röntgen
— Θεωρία της
σχετικότητας – Einstein — Η αυγή της θεωρίας των κβάντα – Planck, Einstein — Έρευνες για τη ραδιενέργεια – Curie — Έρευνες
για τη σύσταση του ατόμου – Rutherford — Ατομικό μοντέλο του Bohr — Ανάπτυξη κβαντικής φυσικής
– Bohr, Pauli, Heisenberg, Schrödinger, Dirac, Bohm —
Ανακάλυψη της “φυγής των γαλαξιών” από τον Hubble — Όρια λογικής –
Gödel — Θεμέλια υπολογιστών – Turing, von Neumann —
Πυρηνική ενέργεια – τί είναι η ατομική βόμβα, και
τί η βόμβα υδρογόνου — Ανακάλυψη δομής DNA
– Crick, Watson — Έξοδος στο διάστημα — Ανάπτυξη νέων τηλεσκοπίων &
άλλων αστρονομικών οργάνων — Συζήτηση: υπάρχει τίποτε σταθερό στην
επιστήμη ή όλα κάποτε καταρρίπτονται;
(κλικ εδώ για αναλυτικές σημειώσεις): Προεπιστήμονες (“φυσικοί φιλόσοφοι”) της αρχαίας
Ελλάδας – ποια η διαφορά με
όλη την προηγούμενη αρχαία σκέψη – Θαλής, Αναξίμανδρος, Αναξιμένης, Πυθαγόρας, Ηράκλειτος,
Εμπεδοκλής, Δημόκριτος,
Πλάτων, Αριστοτέλης, Αρίσταρχος ο
Σάμιος — Αρχαίοι Έλληνες
μαθηματικοί και εφευρέτες – Αρχιμήδης,
Ερατοσθένης — Σημασία της Ευκλείδειας γεωμετρίας
στο συνολικό οικοδόμημα της επιστήμης — Αλχημιστές του Μεσαίωνα –
πού έκαναν λάθος — Κοπέρνικος – ηλιοκεντρικό αντί γεωκεντρικό σύστημα,
ξυράφι του Ockham — Η αυγή της επιστημονικής σκέψης – Γαλιλαίος —
René Descartes – Καρτεσιανές συντεταγμένες — Αρχή μαθηματικής ανάλυσης –
Newton, Leibniz — Κλασική φυσική – Newton — Μικροσκόπιο – van Leeuwenhoek, Hooke — Νεότερη ατομική θεωρία – Dalton —
Πρόοδος μαθηματικών και μη
ευκλείδειες γεωμετρίες – Gauss — Ηλεκτρομαγνητική θεωρία – Faraday,
Maxwell — Θεωρία της εξέλιξης των ειδών – Darwin, Wallace — Περιοδικός πίνακας – Mendeleev —
Ανακάλυψη ακτίνων Χ – Röntgen
— Θεωρία της
σχετικότητας – Einstein — Η αυγή της θεωρίας των κβάντα – Planck, Einstein — Έρευνες για τη ραδιενέργεια – Curie — Έρευνες
για τη σύσταση του ατόμου – Rutherford — Ατομικό μοντέλο του Bohr — Ανάπτυξη κβαντικής φυσικής
– Bohr, Pauli, Heisenberg, Schrödinger, Dirac, Bohm —
Ανακάλυψη της “φυγής των γαλαξιών” από τον Hubble — Όρια λογικής –
Gödel — Θεμέλια υπολογιστών – Turing, von Neumann —
Πυρηνική ενέργεια – τί είναι η ατομική βόμβα, και
τί η βόμβα υδρογόνου — Ανακάλυψη δομής DNA
– Crick, Watson — Έξοδος στο διάστημα — Ανάπτυξη νέων τηλεσκοπίων &
άλλων αστρονομικών οργάνων — Συζήτηση: υπάρχει τίποτε σταθερό στην
επιστήμη ή όλα κάποτε καταρρίπτονται;
Κ1. Εξέλιξη Σύμπαντος: Γενίκευση της έννοιας “χώρος” — Τί είναι ο χώρος τεσσάρων διαστάσεων —Τί είναι ένας καμπύλος χώρος — Πού είναι το κέντρο του σύμπαντος; – γιατί ο τριδιάστατος χώρος δεν έχει κέντρο — Μπορεί να υπάρχει “έξω” από το σύμπαν; — Γεωδεσιακές και φωτόνια — Τί είναι η “Μεγάλη Έκκρηξη” – η “φυγή” των γαλαξιών – φαινόμενο Doppler – η ανακάλυψη του Edwin Hubble – κοσμική ακτινοβολία μικροκυμάτων — Γιατί η ταχύτητα του φωτός δεν αποτελεί τροχοπέδη της διαστολής του χωροχρόνου — Παρατηρήσιμος ορίζοντας – μπορούν να υπάρχουν άλλα σύμπαντα; — Τί είδους “κέντρο” μπορεί να έχει ένα τετραδιάστατο χωροχρονικό συνεχές; — Σύσταση του σύμπαντος ανά χρονική περίοδο – εκθετική επιτάχυνση (ή επιβράδυνση) της σπουδαιότητας των γεγονότων — Νεότερες ανακαλύψεις σχετικά με το μέλλον του σύμπαντος – επιταχυνόμενη διαστολή.
Μ1. Αποδεικτική Μέθοδος
![]()
![]() (κλικ εδώ για αναλυτικές σημειώσεις) (υποχρεωτικό
προαπαιτούμενο όλων των μαθηματικών, και προτεινόμενο
προαπαιτούμενο όλων): Τί είναι μια απόδειξη — Ο θεμελιώδης λογικός
κανόνας modus ponens — ο κανόνας modus tollens — Απαγωγή σε άτοπο — Τα
παραλειπόμενα “προφανή” σημεία των αποδείξεων — Δομή απόδειξης –
κατευθυνόμενα ακυκλικά γραφήματα — Παραδείγματα: από την Ευκλείδεια
γεωμετρία – από τη στοιχειώδη θεωρία συνόλων – από την αριθμητική (αξιώματα
Peano) – από τη λογική (λογικοί τύποι, ταυτολογίες).
(κλικ εδώ για αναλυτικές σημειώσεις) (υποχρεωτικό
προαπαιτούμενο όλων των μαθηματικών, και προτεινόμενο
προαπαιτούμενο όλων): Τί είναι μια απόδειξη — Ο θεμελιώδης λογικός
κανόνας modus ponens — ο κανόνας modus tollens — Απαγωγή σε άτοπο — Τα
παραλειπόμενα “προφανή” σημεία των αποδείξεων — Δομή απόδειξης –
κατευθυνόμενα ακυκλικά γραφήματα — Παραδείγματα: από την Ευκλείδεια
γεωμετρία – από τη στοιχειώδη θεωρία συνόλων – από την αριθμητική (αξιώματα
Peano) – από τη λογική (λογικοί τύποι, ταυτολογίες).
Μ2. Λογική: Λογικές μεταβλητές, λογικοί τελεστές,
πίνακες αλήθειας — Εξαρτήσεις τελεστών από άλλους – ισοδυναμίες —
Προτασιακός λογισμός – ερμηνεία τύπων – κανονικές μορφές —
Κατηγορηματικός λογισμός — Πρωτοβάθμια λογική – αλφάβητα, όροι, τύποι —
Επαγωγή — Ελεύθερες μεταβλητές και προτάσεις — Δομές και ερμηνείες — Οι
σχέσεις ικανοποίησης και συνεπαγωγής — Αντικατάσταση όρων — Θεώρημα
πληρότητας — Το “εύρος” της πρωτοβάθμιας λογικής — Δευτεροβάθμια λογική
— Περιορισμοί της λογικής μεθόδου – απαριθμησιμότητα και αποφασισιμότητα
— Το θεώρημα μη-πληρότητας του Gödel — Προαιρετικό:
Αυτόματη απόδειξη θεωρημάτων —
Άλλες λογικές, διάφορες της “κλασικής”.
Μ3. Γεωμετρίες (Ευκλείδεια – Μη Ευκλείδειες):
Τα «Στοιχεία» του Ευκλείδη και τα 5 αιτήματα — Αξιώματα και κοινές
έννοιες — Θεωρήματα και παραδείγματα αποδείξεων —
Τα παραλειπόμενα
“προφανή” σημεία των αποδείξεων, και αυτά που παρέλειψε ο Ευκλείδης —
Προσπάθειες να αποδειχθεί το 5ο αίτημα του Ευκλείδη (ιστορική αναδρομή)
— Ανακάλυψη μη Ευκλείδειων γεωμετριών – Bolyai, Gauss, Lobachevsky,
Riemann – συνέπειες για τη θεωρία της σχετικότητας — Εξέταση σφαιρικής
και υπερβολικής γεωμετρίας — Η έννοια της μετρικής του χώρου —
Προαιρετικό: Αναλυτική γεωμετρία — Προαιρετικό: Γεωμετρία του τριγώνου.
Μ4. Απειροστικός Λογισμός: Συναρτήσεις —
Πολυωνυμικές, εκθετικές, λογαριθμικές, τριγωνομετρικές, και αντίστροφες
τριγ. συναρτήσεις — Όρια — Παράγωγος – αναδρομικός κανόνας – θεώρημα
μέσης τιμής — Συνεχείς συναρτήσεις — Δεύτερη παράγωγος –
μέγιστα-ελάχιστα, σημεία καμπής, ασύμπτωτοι, κανόνας L’Hôpital,
σχηματισμός γραφήματος — Πολικές συντεταγμένες — Ολοκληρώματα – αόριστα
και ορισμένα – επιφάνεια υπό καμπύλη — Ολοκλήρωση με αντικατάσταση και
ολοκλήρωση κατά μέρη — Πολλαπλά ολοκληρώματα – εφαρμογές: όγκος, μάζα,
επιφάνεια — Γραμμικά ολοκληρώματα – παραμετρική παράσταση καμπύλης –
εφαρμογές: έργο, μήκος καμπύλης — Επιφανειακά ολοκληρώματα – παραμετρική
παράσταση επιφάνειας.
Μ5. Γραμμική Άλγεβρα: Διανύσματα και πίνακες — Γραμμικά συστήματα ως πίνακες – μέθοδος απαλοιφής του Gauss – αδύνατη λύση, άπειρες λύσεις – βάση και διάσταση — Άλγεβρα πινάκων – πρόσθεση, πολλαπλασιασμός, ανάστροφος πίνακα, αντίστροφος τετραγωνικού πίνακα — Διακρίνουσες – υπολογισμός, γινόμενο — Ανεξαρτησία διανυσμάτων — Κανόνας του Cramer — Γραμμικοί χώροι — Εσωτερικό και εξωτερικό γινόμενο — Ευκλείδειοι χώροι — Νόρμες — Ορθογωνιότητα σε Ευκλείδειους χώρους — Στροφή συνάρτησης σε Ευκλείδειο χώρο — Ιδιοτιμές και ιδιοδιανύσματα – πολλαπλότητα — Χαρακτηριστικό πολυώνυμο — Ίχνος πίνακα — Πυρήνας πίνακα — Όμοιοι πίνακες — Συμμετρικοί και Ερμητιανοί τελεστές — Ορθοκανονικά ιδιοδιανύσματα για Ερμητιανούς τελεστές — Διαγωνιοποίηση Ερμητιανών πινάκων — Τετραγωνικές μορφές – εφαρμογή στην αναλυτική γεωμετρία.
Μ6. Μιγαδικοί Αριθμοί: Ορισμός και κίνητρο ύπαρξης μιγαδικών — Πράξεις — Συζυγής μιγαδικός — Γεωμετρική παράσταση — Μέτρο και όρισμα — Ρίζες της μονάδας — Μιγαδικοί εκθέτες — Η εντυπωσιακότερη μαθηματική σχέση που υπήρξε ποτέ (eiπ = –1) — Συναρτήσεις μιγαδικών μεταβλητών — Παραγώγιση και ολοκλήρωση μιγαδικών συναρτήσεων.
Μ7. Θεωρία Συνόλων: Σύνολα και
πράξεις συνόλων — Σχέσεις, συναρτήσεις, και διατάξεις — Φυσικοί αριθμοί
— Πεπερασμένα, μετρήσιμα, και μη μετρήσιμα σύνολα — Διατακτικοί αριθμοί
και πληθάριθμοι — Ακέραιοι και ρητοί αριθμοί – απόδειξη μετρησιμότητας —
Άρρητοι και πραγματικοί αριθμοί – απόδειξη μη μετρησιμότητας — —
Υπερβατικοί αριθμοί – τί είναι η ρίζα του 2; τί ο π και ο e; —
Υπερσύνολα και υποσύνολα πραγματικών αριθμών – δυναμοσύνολο συνόλου –
μιγαδικοί αριθμοί — Ο πληθάριθμος του συνεχούς — Αριθμοί Άλεφ.
Μ8. Θεωρία Αριθμών: Οι θετικοί ακέραιοι —
το σύνολο Ζ των ακεραίων — Διαιρετότητα και διαιρέτες — Ελάχιστο
κοινό πολλαπλάσιο, μέγιστος κοινός διαιρέτης και ο Ευκλείδειος
αλγόριθμος — Πρώτοι αριθμοί – Ευκλείδεια απόδειξη άπειρου πλήθους —
Ανάλυση σε πρώτους παράγοντες – το θεμελιώδες θεώρημα της αριθμητικής —
Αριθμοί πρώτοι προς αλλήλους — Η συνάρτηση φ του Euler — Ισοτιμίες –
πράξεις ισοτιμιών — Συστήματα καταλοίπων mod m — Θεώρημα του Euler –
τάξη του a mod m — Γραμμικές ισοτιμίες — Οι ρητοί αριθμοί — Αλγεβρικές
δομές – ημιομάδα, ομάδα, δακτύλιος, ακέραια περιοχή, σώμα — Ο δακτύλιος
των κλάσεων ισοτιμίας mod m — Αλγεβρικές ισοτιμίες και αρχικές ρίζες —
Τετραγωνικά κατάλοιπα — Διοφαντικές εξισώσεις — Τελευταίο θεώρημα του
Fermat.
Μ9. Εισαγωγή στην Τοπολογία: Τί είναι τα πολύεδρα – ανασκόπηση — Ο τύπος του Euler – στερεά με οπές — Απόδειξη οτι υπάρχουν ακριβώς πέντε Πλατωνικά πολύεδρα — Fullerenes – γεωδεσιακοί θόλοι — Οι προσπάθειες των Descartes και Legendre – γεωδεσιακά τρίγωνα – θεώρημα των Harriot-Girard – γεωδεσιακά πολύγωνα — Γράφοι – οι γέφυρες του Königsberg – διαδρομές Euler — Επιπεδοποιημένα πολύεδρα και η απόδειξη του Cauchy — Γράφοι – επίπεδοι, πλήρεις, διμερείς – διακριτό εμβαδόν — Θεώρημα των τεσσάρων χρωμάτων – μεταφορά σε πρόβλημα γράφων – αποδείξεις μέσω υπολογιστών — Ορισμός πολυέδρων Euler — Επιφάνειες – εξωτερική και εσωτερική διάσταση – κλειστές και συμπαγείς επιφάνειες – συγκολλήσεις επιφανειών και τοπολογικοί ισομορφισμοί – η λωρίδα του Möbius – μη προσανατολίσιμες επιφάνειες – η φιάλη του Klein – το προβολικό επίπεδο και το σταυρωτό καπέλλο – γένος επιφάνειας — Τοπολογικοί ομοιομορφισμοί και αναλλοίωτες ιδιότητες – ταξινόμηση επιφανειών — Κόμβοι – επιφάνειες Seifert – γένος κόμβου – πρώτοι μεταξύ κόμβων – άλλες αναλλοίωτες ιδιότητες κόμβων — Διανυσματικά πεδία – κρίσιμα σημεία και δείκτες – θεώρημα Poincaré-Hopf — Σχέση μεταξύ τοπολογίας και γεωμετρίας – καμπυλότητα Gauss – τοπικό και καθολικό θεώρημα Gauss-Bonnet — Γενίκευση σε ν-διαστάσεις.
Μ10. Πιθανότητες – Στατιστική: Τί είναι η πιθανότητα — Πειράματα τύχης — Ανεξάρτητα και εξαρτημένα γεγονότα — Δεσμευμένη πιθανότητα — Γινόμενο και άθροισμα πιθανοτήτων – συμπλήρωμα πιθανότητας — Κανόνας του Bayes — Κατανομές πιθανοτήτων – συνεχείς και διακριτές — Μέση τιμή και διασπορά — Μαθηματική ελπίδα — Διωνυμική κατανομή — Ομοιόμορφη κατανομή — Κανονική κατανομή — Κατανομή t του Student — Κατανομή χ2 — Κατανομή F — Δειγματοληψία – ιστογράμματα — Δειγματοληπτική κατανομή μέσης τιμής, λόγου, και διαφοράς μέσων τιμών — Εκτιμητική — Εκτίμηση μέσης τιμής πληθυσμού με γνωστή διασπορά — Έλεγχος υποθέσεων — Έλεγχος υπόθεσης για μέση τιμή πληθυσμού με γνωστή διασπορά — Σφάλματα τύπου Ι και τύπου ΙΙ — Έλεγχος υπόθεσης για μέση τιμή πληθυσμού με άγνωστη διασπορά — Εκτίμηση διασποράς — Εκτίμηση λόγου — Εκτίμηση διαφοράς μέσων τιμών – μέθοδος αντίστοιχων ζευγών — Εκτίμηση λόγου διασπορών — Εκτίμηση διαφοράς δύο λόγων — Ανάλυση διασποράς (ANOVA) — Έλεγχος χ2 — Μη παραμετρικές στατιστικές μέθοδοι — Γραμμική παλινδρόμηση και συσχέτιση – συντελεστής συσχέτισης — Πολλαπλή παλινδρόμηση.
Μ11. Αριθμητική Ανάλυση: Λύση γενικών αλγεβρικών (μη γραμμικών) εξισώσεων – μέθοδος τέμνουσας – μέθοδος Newton-Raphson μέσω παραγώγου – ρίζες πολυωνύμων — Λύση γραμμικών συστημάτων – απαλοιφή Gauss-Jordan – αποσύνθεση LU – αντίστροφος πίνακα – διακρίνουσα πίνακα – τριδιαγώνια συστήματα εξισώσεων – αραιά γραμμικά συστήματα — Ολοκλήρωση συναρτήσεων – μέθοδος τραπεζίου – μέθοδος Simpson – γενικευμένα ολοκληρώματα – μέθοδος Gauss – πολυδιάστατα ολοκληρώματα — Τυχαίοι αριθμοί – μέθοδοι modulo N και προβλήματα – ομοιόμορφη κατανομή – κανονική κατανομή – κρυπτογραφία – μέθοδοι Monte Carlo — Παρεμβολή (interpolation) και παρέκταση (extrapolation) συναρτήσεων – πολυώνυμα – ρητές συναρτήσεις – παρεμβολή κυβικών splines – δύο ή περισσότερες διαστάσεις — Υπολογισμός συναρτήσεων – σειρές και σύγκλιση – συνεχιζόμενα κλάσματα – πολυώνυμα και ρητές συναρτήσεις – αναδρομικές σχέσεις – δευτεροβάθμιες & τριτοβάθμιες εξισώσεις – προσέγγιση κατά Chebyshev — Ειδικές συναρτήσεις – συνάρτηση γάμμα, βήτα, παραγοντική, διωνυμικοί τελεστές — Ταξινόμηση – κατευθείαν εισαγωγή, bubblesort, heapsort, quicksort — Ελαχιστοποίηση και Μεγιστοποίηση συναρτήσεων – γραμμικός προγραμματισμός και μέθοδος simplex — Ιδιοτιμές και ιδιοδιανύσματα – τριδιαγώνιοι πίνακες – Ερμιτιανοί πίνακες — Μετασχηματισμοί Fourier – σε διακριτά δεδομένα – γρήγοροι μετασχηματισμοί Fourier — Μοντέλα δεδομένων – μέθοδος ελάχιστων τετραγώνων – γραμμική προσέγγιση δεδομένων – ελάχιστα τετράγωνα σε ν διαστάσεις – μη γραμμικές μέθοδοι — Λύση συνήθων διαφορικών εξισώσεων – μέθοδος Runge-Kutta.
Ν1. Εισαγωγή στη Νοολογία ![]()
![]() (κλικ εδώ για αναλυτικές σημειώσεις):
Με τί ασχολείται η νοολογία – γιατί ονομάζεται έτσι – οι πέντε κύριοι τομείς
γνώσεις που περιλαμβάνει η νοολογία, αλλά και άλλοι σχετιζόμενοι.
(κλικ εδώ για αναλυτικές σημειώσεις):
Με τί ασχολείται η νοολογία – γιατί ονομάζεται έτσι – οι πέντε κύριοι τομείς
γνώσεις που περιλαμβάνει η νοολογία, αλλά και άλλοι σχετιζόμενοι.
Ν2. Νους – Έννοιες ![]()
![]() (κλικ εδώ για αναλυτικές σημειώσεις):
Στόχος του μαθήματος και η κεντρική υπόθεση της
νοολογίας — Η έννοια της έννοιας:
θεωρίες
για τη φύση των εννοιών – Πλάτων, και η κλασική θεωρία – Αριστοτέλης,
και η αναλυτική θεωρία – κριτική της κλασικής
θεωρίας περί ορισμών – θεωρία
προτύπου, και το μοντέλο πυρήνα-υπολοίπου –
κριτική των θεωριών προτύπου και πυρήνα-υπολοίπου – θεωρία παραδειγμάτων
— Πρώτος νόμος: Κατηγοριοποίηση –
η έννοια της
απόστασης των εννοιών – διαστάσεις – ομοιότητα –
το “Μοντέλο Γενικευμένου Περιβάλλοντος”
(GCM) –
προέλευση του πρώτου νόμου –
ένα φιλοσοφικό ερώτημα — Δεύτερος νόμος: Ταυτοποίηση πυρήνα –
ο θεμελιώδης ρόλος
της αναλογίας στην ανθρώπινη νόηση —
Τρίτος νόμος: Συμπλήρωση μοτίβου –
ο ρόλος της πρόβλεψης στη νόηση —
Τέταρτος νόμος: Ξυράφι του Ockham – ελαχιστοποίηση δομών —
Πέμπτος νόμος: Ποσοτική αντίληψη —
Έκτος νόμος: Δημιουργία συσχετισμών μέσω παράθεσης — Γιατί ξεχνάμε —
Συζήτηση: Μπορεί να υπάρξει άυλος νους;
(κλικ εδώ για αναλυτικές σημειώσεις):
Στόχος του μαθήματος και η κεντρική υπόθεση της
νοολογίας — Η έννοια της έννοιας:
θεωρίες
για τη φύση των εννοιών – Πλάτων, και η κλασική θεωρία – Αριστοτέλης,
και η αναλυτική θεωρία – κριτική της κλασικής
θεωρίας περί ορισμών – θεωρία
προτύπου, και το μοντέλο πυρήνα-υπολοίπου –
κριτική των θεωριών προτύπου και πυρήνα-υπολοίπου – θεωρία παραδειγμάτων
— Πρώτος νόμος: Κατηγοριοποίηση –
η έννοια της
απόστασης των εννοιών – διαστάσεις – ομοιότητα –
το “Μοντέλο Γενικευμένου Περιβάλλοντος”
(GCM) –
προέλευση του πρώτου νόμου –
ένα φιλοσοφικό ερώτημα — Δεύτερος νόμος: Ταυτοποίηση πυρήνα –
ο θεμελιώδης ρόλος
της αναλογίας στην ανθρώπινη νόηση —
Τρίτος νόμος: Συμπλήρωση μοτίβου –
ο ρόλος της πρόβλεψης στη νόηση —
Τέταρτος νόμος: Ξυράφι του Ockham – ελαχιστοποίηση δομών —
Πέμπτος νόμος: Ποσοτική αντίληψη —
Έκτος νόμος: Δημιουργία συσχετισμών μέσω παράθεσης — Γιατί ξεχνάμε —
Συζήτηση: Μπορεί να υπάρξει άυλος νους;
Ν3. Εγκέφαλος – Νευρώνες: Τί είναι οι νευρώνες — Μεμβράνες και δυναμικά — Η σύναψη – διάδοση σήματος στη σύναψη — Νευροδιαβιβαστές — Πού είναι η μνήμη; — Χημικά κυκλώματα — Πεπτίδια και ορμόνες — Ναρκωτικά, καφεΐνη, νικοτίνη, και οινόπνευμα – τί αποτέλεσμα έχουν σε επίπεδο νευρώνων — Συνδέσεις του υποθαλάμου — Ο οπτικός φλοιός και το μάτι — Ο ακουστικός φλοιός και το αυτί — Ο κινητικός φλοιός — Ο αισθητικός φλοιός — Κέντρα όσφρησης — Κέντρα επεξεργασίας της γλώσσας — Κέντρα συναισθημάτων – το κέντρο του “Θεού”; — Κέντρα αίσθησης χώρου και ορίων του σώματος – διαλογισμός — Κέντρα ορθολογικής σκέψης — Κέντρα που καθορίζουν χαρακτηριστικά της προσωπικότητας – η παράξενη περίπτωση του Phineas Gage — Η σύνδεση των δύο ημισφαιρίων, και τί συμβαίνει όταν διαχωρίζονται.
Ν4. Σχέση Νου –
Εγκεφάλου ![]()
![]() (κλικ εδώ για αναλυτικές σημειώσεις): Σύντομη ανασκόπηση προαπαιτούμενης γνώσης από το μάθημα
Ν1 – νευρώνες – συνάψεις – μνήμη, μάθηση – λοβοί και άλλα μέρη εγκεφάλου —
Σχιζοφρένεια, νόσος Πάρκινσον, και κατάθλιψη — Εξάρτηση και αλλοίωση της σκέψης από χημικές ουσίες:
μορφίνη και οπιοειδή – συστήματα πόνου και ευχαρίστησης – η επίδραση της
καφεΐνης, νικοτίνης, αλκοόλ, και διαφόρων ναρκωτικών ουσιών – εθισμός,
εξάρτηση, ανοχή, στέρηση — Παραισθήσεις – σύνδρομο Σαρλ Μπονέ –
σκοτώματα και το τυφλό σημείο – πώς βλέπουμε – ακουστικές και μουσικές
παραισθήσεις – παραισθήσεις λόγω καταπόνησης του οργανισμού — Αγνωσίες – αχρωματοψία
(αγνωσία χρώματος) – ακινητοψία (αγνωσία κίνησης) – προσωπαγνωσία –
σύνδρομο Κάπγκρας – δυσαριθμησία και αναριθμησία – αγνωσία χωρικής
πλοήγησης και χρονικής διάρκειας — Γλωσσικές ανωμαλίες – δυσλεξία — Ο
ρόλος του ιππόκαμπου στη μνήμη μακράς διαρκείας — Το μάθημα αυτό περιλαμβάνει επιλεγμένα αναγνώσματα από τα
βιβλία: (1) «Φαντάσματα
στον εγκέφαλο» (2005) των
V. S. Ramachandran & Sandra Blakeslee,
(2) «Descartes’
Error» (2006) του
Antonio Damasio, (3) «The
Language Instinct» (1994) του
Steven Pinker, (4) «How
the Mind Works» (1997) επίσης του Steven
Pinker, και (5)
Μουσικοφιλία (2011) του Oliver Sacks.
(κλικ εδώ για αναλυτικές σημειώσεις): Σύντομη ανασκόπηση προαπαιτούμενης γνώσης από το μάθημα
Ν1 – νευρώνες – συνάψεις – μνήμη, μάθηση – λοβοί και άλλα μέρη εγκεφάλου —
Σχιζοφρένεια, νόσος Πάρκινσον, και κατάθλιψη — Εξάρτηση και αλλοίωση της σκέψης από χημικές ουσίες:
μορφίνη και οπιοειδή – συστήματα πόνου και ευχαρίστησης – η επίδραση της
καφεΐνης, νικοτίνης, αλκοόλ, και διαφόρων ναρκωτικών ουσιών – εθισμός,
εξάρτηση, ανοχή, στέρηση — Παραισθήσεις – σύνδρομο Σαρλ Μπονέ –
σκοτώματα και το τυφλό σημείο – πώς βλέπουμε – ακουστικές και μουσικές
παραισθήσεις – παραισθήσεις λόγω καταπόνησης του οργανισμού — Αγνωσίες – αχρωματοψία
(αγνωσία χρώματος) – ακινητοψία (αγνωσία κίνησης) – προσωπαγνωσία –
σύνδρομο Κάπγκρας – δυσαριθμησία και αναριθμησία – αγνωσία χωρικής
πλοήγησης και χρονικής διάρκειας — Γλωσσικές ανωμαλίες – δυσλεξία — Ο
ρόλος του ιππόκαμπου στη μνήμη μακράς διαρκείας — Το μάθημα αυτό περιλαμβάνει επιλεγμένα αναγνώσματα από τα
βιβλία: (1) «Φαντάσματα
στον εγκέφαλο» (2005) των
V. S. Ramachandran & Sandra Blakeslee,
(2) «Descartes’
Error» (2006) του
Antonio Damasio, (3) «The
Language Instinct» (1994) του
Steven Pinker, (4) «How
the Mind Works» (1997) επίσης του Steven
Pinker, και (5)
Μουσικοφιλία (2011) του Oliver Sacks.
Ν5. Αρχιτεκτονική Νου κατά Hofstadter: Προέλευση των εννοιών: άνθρωπος και όραση – βάση των αφηρημένων εννοιών στην όραση – η όραση των ζώων – η ανθρώπινη όραση – ο οπτικός φλοιός του εγκεφάλου – νευρώνες απλοί, σύνθετοι, και πολυσύνθετοι – δίδαγμα: το “όλον” αναλύεται σε μεγάλο αριθμό στοιχειωδών μερών — Πώς μπορούν να χτίζονται οι έννοιες από στοιχειώδη μέρη – η αρχή της διασύνδεσης – μάθηση Hebb — Αρχιτεκτονική του νου σύμφωνα με την ερευνητική ομάδα του Hofstadter — Μνήμη εργασίας – οι σκέψεις “χτίζονται” στη μνήμη εργασίας – κωδικάρια (“codelets”) και ο κωδικοσυρμός (“coderack”) – παράλληλη σάρωση – “θερμοκρασία” δομών — Μνήμη μακράς διαρκείας – το “γλιστροδίκτυο” (“slipnet”) – η έννοια του “γλιστρήματος” (“slippage”) εννοιών — Αναλογίες και ο ρόλος που παίζουν στην ανθρώπινη νόηση.
Υ1.
Θεμελιώδεις Έννοιες Υπολογιστών: Διαφορά αναλογικής και ψηφιακής
πληροφορίας — Τί είναι το bit – σύνδεση με λογική – λογικές πράξεις:
και, ή, όχι – πίνακες αλήθειας — Τί είναι το byte και τί το word —
Αλγόριθμοι και προγράμματα – παράδειγμα αλγορίθμου – γλώσσα μηχανής –
γλώσσα assembler – γλώσσες προγραμματισμού — Πού αποθηκεύονται τα
προγράμματα — Hardware και αρχιτεκτονική von Neumann – πόσα πραγματικά
διαφορετικά είδη υπολογιστών υπάρχουν; — Μέρη υπολογιστή: κεντρικός
επεξεργαστής, κύρια μνήμη, περιφερειακή μνήμη, οθόνη, περιφερειακές
συσκευές — Λογισμικό (software) — Πώς ξεκινάει ένας υπολογιστής — Τί
είναι το λειτουργικό σύστημα – παραδείγματα: Windows, Mac OS, Unix &
Linux — Τί είναι τα προγράμματα εφαρμογών — Πόσα πραγματικά διαφορετικά
είδη προγραμμάτων υπάρχουν; – μηχανές Turing.
Υ2. Προγραμματισμός ![]()
![]() (κλικ
εδώ για αναλυτικές σημειώσεις): Διαχωρισμός μάθησης
χειρισμού προγραμματιστικού περιβάλλοντος από προγραμματισμό καθαυτό —
Οι τρεις θεμελιώδεις δομές προγραμματισμού – ακολουθία εντολών – λογικός
έλεγχος – επανάληψη ή ανακύκλωση — Προγράμματα γραφικών, ασκήσεις στα
προηγούμενα — Προγράμματα αριμητικής: αριθμός διαιρετός διά 7 ή όχι – λίστα
διαιρετών αριθμού – αριθμός πρώτος ή όχι — Εισαγωγή δεδομένων με χρήση
απλών (έτοιμων) παραθύρων εισαγωγής – αριθμοί πρώτοι προς αλλήλους — Η
έννοια της μεθόδου και της συνάρτησης — Η έννοια της παραμέτρου — Ο
κανόνας της προσπάθειας προς γενίκευση — Απλές δομές δεδομένων – πίνακες
– εγγραφές — Απλά προγράμματα γραφικών –
διαχωρισμός γενικού προγραμματισμού από εξειδικευμένες βιβλιοθήκες
γραφικών — Αντικείμενα που περικλείουν μεθόδους — Τί είναι το
αντικείμενο και τί η τάξη στην οποία ανήκει — Δημιουργία και καταστροφή
αντικειμένων — Ανασκόπηση στοιχείων
διαλόγων εισαγωγής δεδομένων, και πώς χρησιμοποιούνται — Επιλογή ενός
μεγαλύτερου προγραμματιστικού έργου ανάλογα με τα ιδιαίτερα ενδιαφέροντα
του διδασκομένου, και βοήθεια προς υλοποίησή του.
(κλικ
εδώ για αναλυτικές σημειώσεις): Διαχωρισμός μάθησης
χειρισμού προγραμματιστικού περιβάλλοντος από προγραμματισμό καθαυτό —
Οι τρεις θεμελιώδεις δομές προγραμματισμού – ακολουθία εντολών – λογικός
έλεγχος – επανάληψη ή ανακύκλωση — Προγράμματα γραφικών, ασκήσεις στα
προηγούμενα — Προγράμματα αριμητικής: αριθμός διαιρετός διά 7 ή όχι – λίστα
διαιρετών αριθμού – αριθμός πρώτος ή όχι — Εισαγωγή δεδομένων με χρήση
απλών (έτοιμων) παραθύρων εισαγωγής – αριθμοί πρώτοι προς αλλήλους — Η
έννοια της μεθόδου και της συνάρτησης — Η έννοια της παραμέτρου — Ο
κανόνας της προσπάθειας προς γενίκευση — Απλές δομές δεδομένων – πίνακες
– εγγραφές — Απλά προγράμματα γραφικών –
διαχωρισμός γενικού προγραμματισμού από εξειδικευμένες βιβλιοθήκες
γραφικών — Αντικείμενα που περικλείουν μεθόδους — Τί είναι το
αντικείμενο και τί η τάξη στην οποία ανήκει — Δημιουργία και καταστροφή
αντικειμένων — Ανασκόπηση στοιχείων
διαλόγων εισαγωγής δεδομένων, και πώς χρησιμοποιούνται — Επιλογή ενός
μεγαλύτερου προγραμματιστικού έργου ανάλογα με τα ιδιαίτερα ενδιαφέροντα
του διδασκομένου, και βοήθεια προς υλοποίησή του.
Υ3. Δομές
Δεδομένων: Πληροφορία για την οποία αρκεί μία λέξη (word) για
αποθήκευση — Συμβολοσειρές (strings) — Πίνακες – μονοδιάστατοι, διδιάστατοι,
πολυδιάστατοι — Ακολουθιακές δυναμικές δομές – στοίβες – ουρές – λίστες
απλής και διπλής σύνδεσης — Άσκηση: αλγόριθμος ταξινόμησης μέσω
απευθείας εισαγωγής — Επανεξέταση πινάκων, τώρα ως δυναμικών δομών —
Σύνολα – μέσω bitstrings και μέσω λιστών (ή πινάκων) — Δέντρα – δυαδικά
– η έννοια της αναδρομής – πολλαπλής διακλάδωσης – εισαγωγή κλάδου,
επίσκεψη & μεταβολή, διαγραφή κλάδου — Ασκήσεις αναδρομής – παραγοντικό,
ακολουθία Fibonacci, πλήθος στοιχείων δέντρου, ταξινόμηση με δυαδικό
δέντρο — Επανεξέταση στοιβών, ουρών, και λιστών, τώρα ως αναδρομικών
δομών — Γραφήματα – μέσω πινάκων, μέσω δυναμικών δομών — Γραφήματα
κατευθυνόμενα και μη – ακυκλικά και μη – με ετικέττες στις ακμές – η πιο
γενική δομή δεδομένων.
Υ4. Είδη Γλωσσών Προγραμματισμού: Γενική
κατηγοριοποίηση γλωσσών: διαδικαστικές, συναρτησιακές, λογικές – άλλα
είδη: διαγραμμάτων ροής, νευρωνικών δικτύων — Επάρκεια της εντολής
if-goto — Τυπικές διαδικαστικές γλώσσες: FORTRAN, Pascal, C — Δομές
δεδομένων που παρείχαν, και τί εισήγαγε η κάθε μία — Προγραμματισμός με
αντικείμενα – C++, Java — Προγραμματισμός ιστοσελίδων – html, Java
applets, Javascript — Συναρτησιακές γλώσσες – Lisp – η έννοια της
αναδρομής – σημαντικός αριθμός παραδειγμάτων για εξοικείωση — Λογικές
γλώσσες – Prolog – η έννοια της αντικατάστασης και της ενοποίησης —
Προσεγγιστικός υπολογισμός με Τεχνητά Νευρωνικά Δίκτυα – πλεονεκτήματα
και μειονεκτήματα.
Υ5. Αυτόματα –
Τυπικές Γλώσσες – Υπολογισιμότητα ![]()
![]() (κλικ
εδώ για αναλυτικές σημειώσεις): Σύμβολα, αλφάβητα, συμβολοσειρές, και
γλώσσες – Γράφοι και δέντρα – Αποδείξεις μέσω επαγωγής — Τί είναι ένα προκαθορίσιμο πεπερασμένο αυτόματο — Μη
προκαθορίσιμα πεπερασμένα αυτόματα — Κανονικές
εκφράσεις και κανονικά σύνολα — το “λήμμα διόγκωσης” (pumping lemma) για
κανονικά σύνολα — Ιδιότητες κλειστότητας κανονικών συνόλων — Αλγόριθμοι
καθορισμού για κανονικά σύνολα — Γραμματικές Χωρίς Συμφραζόμενα (Γ.Χ.Σ.)
— Δέντρα παραγωγής Γ.Χ.Σ. — Απλοποιήσεις γραμματικών — Κανονικές μορφές
Chomsky και Greibach — Ύπαρξη ενδογενώς διφορούμενων Γ.Χ.Σ. — Το λήμμα
διόγκωσης για Γ.Χ.Σ. — Ιδιότητες κλειστότητας των Γ.Χ.Σ. — Αλγόριθμοι
καθορισμού για Γ.Χ.Σ. — Αυτόματα στοίβας, και σχέση με τις Γ.Χ.Σ. —
Μηχανές Turing (Μ.Τ.) — Υπολογίσιμες γλώσσες και συναρτήσεις —
Παραλλαγές Μ.Τ. – μηχανές τυχαίας πρόσβασης — Η υπόθεση των
Church-Turing — Αναποφασισιμότητα — Ιδιότητες των αναδρομικών και των
αναδρομικά απαριθμήσιμων γλωσσών — Καθολικές Μηχανές Turing – μοντέλα
υπολογιστών — Εισαγωγή στη θεωρία αναδρομικών συναρτήσεων — Η ιεραρχία
Chomsky – κανονικές γραμματικές, γραμματικές με συμφραζόμενα (Γ.Μ.Σ.),
απεριόριστες γραμματικές — Γραμμικά περατωμένα αυτόματα και σχέση με
Γ.Μ.Σ και κοινούς υπολογιστές.
(κλικ
εδώ για αναλυτικές σημειώσεις): Σύμβολα, αλφάβητα, συμβολοσειρές, και
γλώσσες – Γράφοι και δέντρα – Αποδείξεις μέσω επαγωγής — Τί είναι ένα προκαθορίσιμο πεπερασμένο αυτόματο — Μη
προκαθορίσιμα πεπερασμένα αυτόματα — Κανονικές
εκφράσεις και κανονικά σύνολα — το “λήμμα διόγκωσης” (pumping lemma) για
κανονικά σύνολα — Ιδιότητες κλειστότητας κανονικών συνόλων — Αλγόριθμοι
καθορισμού για κανονικά σύνολα — Γραμματικές Χωρίς Συμφραζόμενα (Γ.Χ.Σ.)
— Δέντρα παραγωγής Γ.Χ.Σ. — Απλοποιήσεις γραμματικών — Κανονικές μορφές
Chomsky και Greibach — Ύπαρξη ενδογενώς διφορούμενων Γ.Χ.Σ. — Το λήμμα
διόγκωσης για Γ.Χ.Σ. — Ιδιότητες κλειστότητας των Γ.Χ.Σ. — Αλγόριθμοι
καθορισμού για Γ.Χ.Σ. — Αυτόματα στοίβας, και σχέση με τις Γ.Χ.Σ. —
Μηχανές Turing (Μ.Τ.) — Υπολογίσιμες γλώσσες και συναρτήσεις —
Παραλλαγές Μ.Τ. – μηχανές τυχαίας πρόσβασης — Η υπόθεση των
Church-Turing — Αναποφασισιμότητα — Ιδιότητες των αναδρομικών και των
αναδρομικά απαριθμήσιμων γλωσσών — Καθολικές Μηχανές Turing – μοντέλα
υπολογιστών — Εισαγωγή στη θεωρία αναδρομικών συναρτήσεων — Η ιεραρχία
Chomsky – κανονικές γραμματικές, γραμματικές με συμφραζόμενα (Γ.Μ.Σ.),
απεριόριστες γραμματικές — Γραμμικά περατωμένα αυτόματα και σχέση με
Γ.Μ.Σ και κοινούς υπολογιστές.
Υ6. Κυτταρικά Αυτόματα: Το μάθημα αυτό είναι αυστηρά εργαστηριακό. Περιλαμβάνει κατασκευή από τον διδασκόμενο βασικής “μηχανής” που υλοποιεί ένα διδιάστατο, συνολικό, τοπικιστικό κυτταρικό αυτόματο, συγκεκριμένα το Game of Life του Conway. Στη συνέχεια η μηχανή επεκτείνεται ώστε να υλοποιεί διάφορες άλλες ιδιότητες κυτταρικών αυτομάτων, όπως η μη συνολικότητα (non totalism), η μη τοπικότητα (non localism), οι διάφορες των δύο διαστάσεις (μία, τρεις), οι μη καρτεσιανοί χώροι (π.χ. χώροι κυψελίδων), κλπ. Εξετάζονται έννοιες όπως η χαοτική συμπεριφορά, η σύγκλιση, η απόκλιση, η υπολογισιμότητα, κ.ά.
Υ7. Τεχνητή Νοημοσύνη: Τί είναι η Τεχνητή Νοημοσύνη και σε τί διαφέρει από υπολογιστικές μεθόδους της νοολογίας — Αλγοριθμικά προβλήματα — Η έννοια του χώρου ψαξίματος — Άπληστο ψάξιμο – “ανάβαση λόφου” — Ψάξιμο κατά πλάτος — Ψάξιμο σε βάθος — Ελαχιστοποίηση ψαξίματος – ευρετικές συναρτήσεις – μετρικές —Ψάξιμο Α* — Προσομοιωμένη αποπυράκτωση — Θεωρία παιγνίων – τέλεια και ατελώς αποφασιζόμενα παιχνίδια: όμικρον–χι, σκάκι — Αποκοπή άλφα-βήτα — Παιχνίδια με το στοιχείο της τύχης – τάβλι — Λογική και προτασιακός λογισμός — Κατηγορηματικός λογισμός – όροι, κατηγορήματα, προτάσεις, τελεστές, καθολικός και υπαρξιακός ποσοδείκτης — Αξιώματα, θεωρήματα — Αναγωγή σε Συζευκτικό Κανονικό Τύπο — Απαλοιφή Skolem — Απόδειξη θεωρημάτων μέσω ανάλυσης (resolution) — Πληρότητα — Στρατηγικές ανάλυσης — Πιθανότητες – ο κανόνας του Bayes — Μάθηση – δένδρα αποφάσεων και εκμάθησή τους — Νευρωνικά δίκτυα — Επεξεργασία φυσικής γλώσσας — Ανάλυση εικόνας — Ρομποτική.
Υ8. Εφαρμογή: Ανάπτυξη Συστήματος Αυτόματων Αποδείξεων: Το μάθημα αυτό είναι αυστηρά εργαστηριακό, και σκοπό έχει την κατασκευή μηχανής αυτόματης απόδειξης σε γλώσσα κατηγορηματικού λογισμού (πρωτοβάθμια λογική). “Καλά δομημένοι τύποι” κατηγορηματικού λογισμού — Αλγόριθμος μετατροπής πρότασης σε “Συζευκτικό Κανονικό Τύπο” (“Conjunctive Normal Form”) — Ενοποίηση – αντικαταστάσεις — Απόφανση (Resolution) και η σχέση με τον κανόνα Modus Ponens — Άρνηση θεωρήματος και “εις άτοπο απαγωγή” — Στρατηγικές επιλογής των όρων προκειμένου να επιτύχει η απόδειξη – σύνολο στήριξης – προτίμηση σε μοναδιαίους όρους – συμπερίληψη (subsumption) — η σημασία των αντικαταστάσεων στην τελική απόδειξη – υπολογισμός μέσω απόδειξης — Ημιυπολογισιμότητα του αλγόριθμου της απόφανσης — Γραμμικές αποφάνσεις μέσω όρων Χορν (Horn clauses) και η σημασία-τους – γλώσσα Prolog.
Φ1.
Θεμελιώδεις Αρχές και Εξέλιξη Φυσικής![]()
![]() (κλικ εδώ για αναλυτικές σημειώσεις):
Τί είναι η κλασική φυσική και
σε τί διαφέρει από τη μοντέρνα φυσική — Θεμελιώδεις αρχές — Το πρόβλημα
στη φυσική – τί αναμένουμε από την εκφώνηση ενός προβλήματος – απλοποιητικές
υποθέσεις προκειμένου να γίνει ένας υπολογισμός – αναλυτική σκέψη –
αφαίρεση, πυρήνας προβλήματος — Η εμπειρική μέθοδος
και οι συνέπειές της στη διατύπωση φυσικών νόμων – αρχή διατήρησης της
ενέργειας – αρχή διατήρησης της ορμής, και στην κλασική φυσική της μάζας
— Θεμελιώδεις έννοιες – η έννοια της “δύναμης”: πώς ξεκίνησε και πώς την
αντιλαμβανόμαστε σήμερα – το αυτό για την έννοια “βαρύτητα” – το αυτό για τις έννοιες
“μάζα” και “ενέργεια” – η έννοια του “κύματος” – το αυτό για τις έννοιες
“χώρος” και “χρόνος” — “Πίστη” των φυσικών στην απλότητα και στην
κατανοησιμότητα της φύσης – κλασικά παραδείγματα: Κοπέρνικος, Αϊνστάιν —
Σύγχρονες αντιλήψεις θεωρητικών φυσικών για την ύλη και το σύμπαν – η
“εκδίκηση του Πυθαγόρα”; — Προσπάθειες διατύπωσης μιας ενοποιημένης
“θεωρίας των πάντων”.
(κλικ εδώ για αναλυτικές σημειώσεις):
Τί είναι η κλασική φυσική και
σε τί διαφέρει από τη μοντέρνα φυσική — Θεμελιώδεις αρχές — Το πρόβλημα
στη φυσική – τί αναμένουμε από την εκφώνηση ενός προβλήματος – απλοποιητικές
υποθέσεις προκειμένου να γίνει ένας υπολογισμός – αναλυτική σκέψη –
αφαίρεση, πυρήνας προβλήματος — Η εμπειρική μέθοδος
και οι συνέπειές της στη διατύπωση φυσικών νόμων – αρχή διατήρησης της
ενέργειας – αρχή διατήρησης της ορμής, και στην κλασική φυσική της μάζας
— Θεμελιώδεις έννοιες – η έννοια της “δύναμης”: πώς ξεκίνησε και πώς την
αντιλαμβανόμαστε σήμερα – το αυτό για την έννοια “βαρύτητα” – το αυτό για τις έννοιες
“μάζα” και “ενέργεια” – η έννοια του “κύματος” – το αυτό για τις έννοιες
“χώρος” και “χρόνος” — “Πίστη” των φυσικών στην απλότητα και στην
κατανοησιμότητα της φύσης – κλασικά παραδείγματα: Κοπέρνικος, Αϊνστάιν —
Σύγχρονες αντιλήψεις θεωρητικών φυσικών για την ύλη και το σύμπαν – η
“εκδίκηση του Πυθαγόρα”; — Προσπάθειες διατύπωσης μιας ενοποιημένης
“θεωρίας των πάντων”.
Φ2.
Ειδική
Σχετικότητα και Στοιχεία Γενικής Σχετικότητας![]()
![]() (κλικ εδώ για αναλυτικές σημειώσεις): Γαλιλαιικά (ή
Ευκλείδεια) συστήματα συντεταγμένων 4 διαστάσεων — Αδρανειακά συστήματα
και 1ο αξίωμα της σχετικότητας — Γαλιλαιικοί μετασχηματισμοί — Διατήρηση
της ορμής και διατήρηση της μάζας — Αιθέρας — Το πείραμα των
Michelson–Morley — Προσπάθειες να σωθεί ο αιθέρας – “παρασύρσιμο” αιθέρα
– θεωρίες εκπομπής – συστολή μήκους των FitzGerald & Lorenz — Το 2ο
αξίωμα της σχετικότητας (σταθερότητα ταχύτητας φωτός) – εγκατάλειψη του
αιθέρα από Einstein — Η σχετικότητα του χρόνου – το ταυτόχρονο γεγονότων
– δεν υπάρχει παγκόσμιο (Νευτώνειο) ρολόι – ομοιότητα χρόνου και χώρου
στη σχετικότητα — Διαστολή του χρόνου – συμπεριφορά κινούμενων ρολογιών
– διάσπαση μιονίων – παράδοξο των διδύμων — Συστολή του μήκους –
παράδοξο τραίνου και ληστών — Μετασχηματισμοί Lorenz — Αναλλοίωτη
τετραδιάστατη απόσταση — Χωροχρονικά διαγράμματα – κώνος φωτός —
Σχετικότητα και αιτιότητα — Ισοδυναμία μάζας-ενέργειας — Γενική
σχετικότητα – η αρχή της ισοδυναμίας — Βαρυτική και αδρανειακή μάζα —
Καμπύλωση και μεταβολή προς το ερυθρό φωτός σε βαρυτικό πεδίο – μαύρες
τρύπες — Ο αριθμός π δεν είναι πια ο ίδιος — Βαρυτική διαστολή χρόνου —
Καμπύλωση χωροχρόνου – γεωδεσιακές — Η βαρύτητα σαν γεωμετρία.
(κλικ εδώ για αναλυτικές σημειώσεις): Γαλιλαιικά (ή
Ευκλείδεια) συστήματα συντεταγμένων 4 διαστάσεων — Αδρανειακά συστήματα
και 1ο αξίωμα της σχετικότητας — Γαλιλαιικοί μετασχηματισμοί — Διατήρηση
της ορμής και διατήρηση της μάζας — Αιθέρας — Το πείραμα των
Michelson–Morley — Προσπάθειες να σωθεί ο αιθέρας – “παρασύρσιμο” αιθέρα
– θεωρίες εκπομπής – συστολή μήκους των FitzGerald & Lorenz — Το 2ο
αξίωμα της σχετικότητας (σταθερότητα ταχύτητας φωτός) – εγκατάλειψη του
αιθέρα από Einstein — Η σχετικότητα του χρόνου – το ταυτόχρονο γεγονότων
– δεν υπάρχει παγκόσμιο (Νευτώνειο) ρολόι – ομοιότητα χρόνου και χώρου
στη σχετικότητα — Διαστολή του χρόνου – συμπεριφορά κινούμενων ρολογιών
– διάσπαση μιονίων – παράδοξο των διδύμων — Συστολή του μήκους –
παράδοξο τραίνου και ληστών — Μετασχηματισμοί Lorenz — Αναλλοίωτη
τετραδιάστατη απόσταση — Χωροχρονικά διαγράμματα – κώνος φωτός —
Σχετικότητα και αιτιότητα — Ισοδυναμία μάζας-ενέργειας — Γενική
σχετικότητα – η αρχή της ισοδυναμίας — Βαρυτική και αδρανειακή μάζα —
Καμπύλωση και μεταβολή προς το ερυθρό φωτός σε βαρυτικό πεδίο – μαύρες
τρύπες — Ο αριθμός π δεν είναι πια ο ίδιος — Βαρυτική διαστολή χρόνου —
Καμπύλωση χωροχρόνου – γεωδεσιακές — Η βαρύτητα σαν γεωμετρία.
Φ3. Εισαγωγή στην Κβαντική Φυσική: Πειράματα σκέδασης του Rutherford — Το ατομικό μοντέλο του Bohr — Ηλεκτρόνια και στοιβάδες – απαγορευτική αρχή του Pauli — Πυρήνας – πρωτόνια και νετρόνια — Σωματίδια και κύματα — Πείραμα της διπλής σχισμής — Αρχή της απροσδιοριστίας του Heisenberg — Η εξίσωση του Schrödinger — Η ερμηνεία του Max Born για την κυματοσυνάρτηση — Λεπτόνια – ηλεκτρόνιο, ποζιτρόνιο και αντιύλη, νετρίνο ηλεκτρονίων, μιόνιο, μιονικό νετρίνο, σωμάτιο ταυ, ταυ νετρίνο — Μάζα, φορτίο, σπιν, ημιζωή — Κουάρκ – σύσταση πρωτονίου και νετρονίου – ονομασία (κάτω, πάνω, παράδοξο, γοητευτικό, πυθμένας, κορυφή), και γεύση (ή άρωμα) — Χρώμα, βαρυονικός αριθμός — Μεσόνια, σύνθετα σωματίδια — Φορείς δυνάμεων – βαρυτική, ασθενής, ηλεκτρομαγνητική, ισχυρή αλληλεπίδραση — Γκλουόνια και ιδιότητές τους — Τί είναι “στην πραγματικότητα” ένα πρωτόνιο (ή νετρόνιο) — Διαγράμματα Feynman – φερμιόνια και μποζόνια – πολυεδρική δομή της ύλης – κίνηση σωματιδίων αντίστροφα στο χρόνο — Πιθανότητες και κβαντική φυσική.
Σημειώσεις
-
Η ελληνική γλώσσα χρησιμοποιεί τη λέξη “επιστήμη” με την αρχαία έννοια, δηλαδή “γνώση του επιστητού”. Σήμερα όμως η αρχαία έννοια έχει εξελιχθεί και αποκτήσει πολύ πιο εξειδικευμένο περιεχόμενο. Είναι τραγικό λάθος να νομίζουμε οτι η σημερινή επιστήμη (που περιγράφεται π.χ. από την αγγλική λέξη “science”) είναι απλώς η γνώση του επιστητού, με αποτέλεσμα να ονομάζουμε “επιστήμονα” ένα δικηγόρο, ή ένα θεολόγο. Σήμερα, επιστήμονας μπορεί να ονομάζεται μόνο εκείνος που ακολουθεί και εφαρμόζει την επιστημονική μέθοδο, που εξηγείται αναλυτικά στο μάθημα Ε1, και που οι κεντρικές έννοιές της απεικονίζονται κυκλικά στο λογότυπο του Δ.Ε.Π.: «Παρατήρηση – Πείραμα – Δεδομένα – Θεωρία – Πρόβλεψη – Δημοσίευση».
-
Δεν χρησιμοποιούνται οι όροι “καθηγητής” και “φοιτητής” γιατί παραπέμπουν σε καταστάσεις προς αποφυγή, από την ελληνική πραγματικότητα.
-
Η χρήση κάμερας και από τις δύο πλευρές βοηθάει πολύ στην ποιότητα της επικοινωνίας, δεν είναι όμως εκ των ουκ άνευ. Ο διδάσκων πρέπει απαραίτητα να έχει κάμερα (και φυσικά μικρόφωνο). Ο διδασκόμενος αναμένεται να έχει μικρόφωνο, ως ελάχιστο μέσο. Επίσης, αν τόσο ο διδάσκων όσο και ο διδασκόμενος μένουν στον ίδιο τόπο και συμφωνήσουν και οι δύο, δεν είναι εκ προοιμίου απαραίτητο να είναι μόνο εικονική (διαδικτυακή) η επικοινωνία μεταξύ των δύο· μπορούν να συναντηθούν σε κοινό τόπο, εφόσον το κρίνουν προτιμότερο.
-
Ενδεικτικό της κραυγής αντί της καθαρής σκέψης: μετρήστε τον αριθμό των θαυμαστικών με τα οποία τελειώνει τις γραπτές προτάσεις ο νεο-έλληνας στα διάφορα ιστολόγια. Αντί να πείσει μέσω επιχειρήματος προσπαθεί να πείσει με την ένταση με την οποία διατυπώνει την άποψή του.
