What Does a 4-Dimensional Sphere Look Like?
There is a very real geometric object, realizable within the relativistic geometry of our universe, which has the properties of a sphere in four dimensions (a “4-hypersphere”); what does it look like? (*)
September 2002
Note (to professionals in relevant fields): the text below presents no new or unknown idea in physics or mathematics. The reason for writing it is that the author has struggled to learn the answers to questions such as this one for years, finding no explicit answer in published texts. I am sure I was simply unlucky in coming across the right publication (and the gentle reader may e-mail me the reference that treats precisely this topic, in case they are aware of one), but now that I think I know the answer I wish to share it with the interested reader of this page. Another reason for writing a web page for this topic is that a true 4D-sphere should be shown in animation, and this is what this page does; printed material must necessarily depict everything in still drawings. If you plan to contact me, please read this paragraph at the end of this text.
Since I was in high school I remember trying to visualize 4-dimensional objects. I managed to draw what I thought was a 4D-cube, and then a 4D-tetrahedron, while the case of a 4D-sphere seemed to be too easy to even talk about. It was only a few years later, while in college, when I realized that my early high school 4D-creations were simply the 4D equivalents of 3D objects rendered in four-dimensional Euclidean space. Except, there is a problem: the geometry of our universe is not Euclidean. Around 70 years before my high school adventures Einstein had proposed that the true geometry of our world is not Euclidean, but hyperbolic, having at least four dimensions: the three familiar spatial ones, plus the fourth one which is time. Although a four-dimensional Euclidean geometry with time as the fourth dimension was already known since Galileo Galilei’s time, it was Einstein who showed that the fourth dimension, time, is essentially different from the other three dimensions.(*) Therefore, my early creations were unrealistic.(*) And yet, real 4D-objects have to be constructible, if the relativistic geometry is real. What do they look like?
Before actually drawing a 4D-sphere, let us make two important observations. First, since time is the fourth dimension, every object with four dimensions has to appear as moving with respect to a fixed frame of reference (say, this page). How it moves is a matter that defines its shape in the fourth dimension, but that it moves is without doubt -- else it is merely a familiar “static” 3D-object. And second, since we want to draw a 4D-sphere, we have to generalize the definition of the familiar 3D-sphere in four dimensions. Let us do this now.
- A circle (or: a “hypersphere in two dimensions”) is the locus of points on a plane (2D-space) that have the same distance from a fixed center.
- A sphere (or: a “hypersphere in three dimensions”) is the locus of points in the 3D-space that have the same distance from a fixed center.
- Therefore, by analogy it follows that a 4D-sphere (or: a “hypersphere in four dimensions”) has to be the locus of points in the 4D-space that have the same distance from a fixed center.
Now, a distance in either two or three dimensions is something we are very familiar with. What is distance in four dimensions, though? And what does a point in four dimensions look like?
Let us answer this last question first. A 4D-point must be an entity that includes three spatial coordinates (x,y,z), plus a fourth one, which gives the time t during which the 3D-point (x,y,z) “occurs”. Hence, instead of a 4D-point we will be talking about an event with coordinates (x,y,z,t). Think of an event as a familiar point (x,y,z) which “blinks” once: instantly goes on and off, at time t at that location.
OK, so far our 4D-points, or events, have nothing to do with relativity -- and they were utilized also in the same way by Galilean 4D geometry. Now we’ll define the distance between two events.
The familiar formula that gives the distance d between two 3D-points (x1,y1,z1) and (x2,y2,z2) is:
![]()
To simplify the above formula we’ll replace expressions such as (x1-x2) simply by x. (If the reader has difficulty seeing a single coordinate as standing for a difference of values, they may think of d as giving the distance of point (x,y,z) from the origin (0,0,0)). Thus, the formula is simplified to this one:
![]()
This formula generalizes easily to four dimensions if we remember to subtract the square of time under the square root, rather than add it to the other three squares. This is because space and time are related, according to relativity, as follows:
s = c t
where c is the speed of
light. This equation can be understood as follows: suppose an
event happens at one end-point of a space-interval s; at
that moment, a photon starts from this end-point traveling along s,
and the moment it reaches the other end-point a second event
happens there. The equation says that every such interval of
space s is equivalent to the time t it takes for
light to traverse it. If we square both sides of the above
equation it becomes: s2 = c2t2,
which can also be written as: s2 - c2t2
= 0. Taking the square root on both sides we get: ![]() , which says that the
4D-distance between two events such as the described ones is
zero. This gives a hint for why we need to subtract time from
space. Accordingly, the formula that gives the distance of two
events in four dimensions is:
, which says that the
4D-distance between two events such as the described ones is
zero. This gives a hint for why we need to subtract time from
space. Accordingly, the formula that gives the distance of two
events in four dimensions is:
![]()
Now we need to recall our earlier definition of a 4D-sphere: it is the locus of events (x,y,z,t) that allow d in the above formula to retain a constant value. Therefore, d plays the role of “radius” in our 4D-sphere.
To draw our 4D-sphere we need to depict a number of 3D-spheres as they change in time so that their 3D-points (x,y,z) along with time t satisfy the previous equation. What could the radius of those 3D-spheres be, as a function of time? We can find this relation very easily if we rewrite the previous equation as follows:
![]()
![]()
![]()
This last equation is the one that tells us how the 3D-spheres (projections of the 4D-sphere in 3D-space) that we want to draw depend on time: the left-hand side of the last equation is the 3D-radius of those spheres, while the right-hand side is a function of t that employs two constants: the predetermined radius d of our 4D-sphere, and the speed of light c. We can denote the left-hand side of this equation by r(t), and plot its values against time:
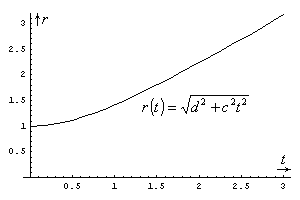
Figure 1: Radius r of time-sliced
3D-spheres as a function of time
The above graph shows how the radius of the “time-sliced” (or: projected) spheres in 3D-space changes as a function of time: initially at time 0 the radius starts from a fixed value d (same d as in our formulas, which we arbitrarily decided to be equal to 1) and changes very slowly, but soon it accelerates and reaches “asymptotically” a nearly constant speed. (We also assumed c = 1 in our graph, to be able to see a sensible curve, rather than c = 299,792.458 km/sec, which is the actual speed of light.) This curve is called a hyperbola, and now it becomes evident why relativistic (read: real-world) geometry is said to be a hyperbolic geometry. We are ready now to plot our 3D-spheres the radius of which changes in time according to the above graph. The whole thing that you see below, as it changes in time, is supposed to be depicting a 4D-sphere:

Figure 2: Animated 4D-sphere
All right. These four seconds of animation (Fig. 2) were arguably what this page is all about. Still, what you see is as incomplete as any rendering of a higher-dimensionality object is on the 2D-plane. So some observations are in order.
First, the “movie” in the image above presumably starts at time equal to “negative infinity”, at which point the time-sliced 3D-sphere has an infinitely large radius. The sphere keeps shrinking until its radius is within the bounds of our box and becomes visible. The shrinking continues up to a minimum at time t = 0, at which point the radius of the time-sliced 3D-sphere is equal to d. Then it starts growing, with time t taking on positive values, exceeding the borders of our box and disappearing from view,(*) and keeps growing forever while time runs to “positive infinity”.
Second, although the 3D-spheres were plotted so that their radius does follow the curve shown in Fig. 1, hence, decelerating its shrinking from an initial near-linear speed and then accelerating until it reaches a near-linear speed again, this behavior can hardly be observed in Fig. 2. The reason is that the curved part of the hyperbola in Fig. 1 happens too fast in Fig. 2, and only at the last few frames before and after reaching the minimum radius d. The reader has to use their imagination to “sense” the non-linear part.
Third, I need to comment on the speed of our animation. If the length of the side of the white box in Fig. 2 is taken to be what it seems to be, namely, a few centimeters, then our animation does not depict a 4D-sphere at all! The reason is that the speed of light is not merely a few centimeters per second, but nearly 30,000,000,000 (thirty American billion) centimeters per second. I used c = 1 in both Fig. 1 & Fig. 2, which corresponds to a very slow speed. Had I used the true value for c, our spheres in Fig. 2 would literally implode and explode at nearly the speed of light! To get an idea about the shape (hence: speed) of the hyperbola for higher values of c, let’s draw again the graph in Fig. 1, this time for c equal to 10 (instead of 1).
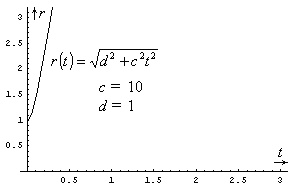
Figure 3: Shape of hyperbola for a
different value of c (c = 10)
We see that with a mere increase of c from 1 to 10 we get a rather sharp hyperbola (therefore, our spheres would shrink and grow rather fast). It’s clearly beyond my visualization abilities to think what the corresponding cases would be for the true c (the speed of light). I can understand such things only as numbers.
Another way to think about what the animation in Fig. 2 shows is this: suppose the white area represented by the box in Fig. 2 is not just a few centimeters, but hundreds of thousands of kilometers wide. In other words, our box can show an area of space engulfing the Earth, the Moon, and a little more. In this way, by increasing enormously the area our box represents, one could think that the speed of shrinking and expansion of the sphere that we observe in Fig. 2 could really be close to the speed of light. Can this idea be right?
Not quite. See, when we look through large expanses of space, the relativistic nature of our universe becomes evident. In our case, the photons from the front portions of the 3D-spheres would arrive to our retinas earlier than the photons from the back parts. (That’s still true if the space covered by the box is small, but the difference is negligible.) This would result in seeing distorted 3D-spheres, with their front parts being ahead of the back parts in implosion and explosion. The larger the 3D-space involved, the worse the distortion.
Now, I would really like to know the answers to the following questions (but please read the explanation of what I want, after the bullets):
- Is the 4D-“volume” of a 4D-sphere finite or infinite? Note that the 4D-sphere is clearly a bounded object,(*) but how we compute the 4D-“volume” in such a geometry? How we integrate when the metric is not the usual Euclidean one? (If you know the answer, please tell me.)
- What is a 4D-cube in relativistic geometry? A tetrahedron?
If you plan to contact me to help me answer the above questions, please note the following. Many people have contacted me over the years during which this page appears on the web, thinking they know the answers. Invariably, I am referred to web pages or to drawings that deal with the 4th dimension in Euclidean geometry. If you plan to do this, please understand that I am not interested in Euclidean, but in relativistic geometry. The Euclidean 4D-cube, for example, has been known since the ancient times. Here is a drawing of it (thanks to Josi Mason for an initial sketch):
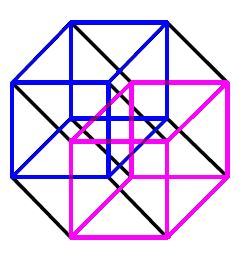
Figure 4: 4D Euclidean cube, known since antiquity. The translated 3D-cube is highlighted within it
The 4D Euclidean cube can be constructed by translating a familiar 3D-cube in an imagined fourth dimension. In antiquity, this 4D Euclidean cube was a mere curiosity (and the adjective “Euclidean” was not attached to it, since nothing non-Euclidean was known.) In our times it has been employed in computer science as a possible topology for a network of parallel processors, where every vertex of it is occupied by a single processor. But my question above concerns its relativistic analogue. Since the relativistic 4D-sphere is an open shape (as opposed to its Euclidean analogue, the 4D Euclidean sphere, which is a closed shape), I expect that the 4D relativistic cube should also be an open shape. Similarly, when I ask about volume, the reader should note that the volume of the 4D Euclidean sphere is well known and easily computable by means of familiar integration (see the formula for the nD-sphere at this footnote(*)). But relativistic geometry has a different metric (its formula is given above) and integration with such a metric uses Legendre integrals, which I am not familiar with. So, I appreciate your paying attention to all this information in case you plan to contact me.
The Best Answer that I Received for the Above Questions
People have kindly responded to my request for answers above, some of them very knowledgeable on the subject. The most comprehensive answer that I have received came from Dr. Eric Hartman, in 2005. For years, I was determined to go through it and understand it thoroughly. Finally I realized I will never find the time to do so, so instead of ignoring his kind offer and the time and effort he invested, I prefer to include it below verbatim, and leave it to the reader to go through it, if interested. Warning: it is long, and does require some familiarity with calculus and relativity.
| Hi Dr. Foundalis, [...] I wanted to take some time to reply to your questions about 4D volumes in Minkowski space:
Let me emphasize that I’m in no way an expert in this area, but from time to time I’ve dabbled in general relativity and related math topics a little bit. But I can at least try to shed some light on your questions. As a natural consequence of the higher dimensional and more complex nature of 4D Minkowski space, there are a number of reasonable interpretations of your questions — ie, answering your question requires sharpening it, and it can be sharpened in a variety of ways. So rather than try to identify a single answer, my goal will be to clarify the issues. I believe that understanding this brief “tutorial” should enable you to pursue such questions as you wish. I’d appreciate knowing if this is helpful, and if you obtain any additional results. I’ll start at square one with the bleeding obvious, because basic ideas have to be sharp to retain one’s footing in unfamiliar geometries. I’ll keep things as simple as possible and bring things up only if they’re really needed. 4-Rectangle Let me start with (4), since the rectangle volume is straightforward. In volume spacetime integrals, the 4-volume element dV4 = dt dx dy dz has a standard orientation (just as does a 3D volume element), in which the time axis points to the future and the xyz axes are right-handed, or equivalently, the integral
⌠⌠⌠⌠
V4 = ││││ dt dx dy dz
⌡⌡⌡⌡
is positive. Therefore, the theory of integration gives the same cartesian volume elements in 4D Minkowski space as it does for 4D Euclidean space,
⌠⌠⌠⌠
V4 = ││││ du dx dy dz
⌡⌡⌡⌡
despite the opposite sign of the fourth component of the cartesian metrics (M4c) ds² = –du² + dx² + dy² + dz² (E4c) ds² = du² + dx² + dy² + dz² With the volume element in standard orientation, the 4-volume integral is simply the same as for (E4c), ∫∫∫∫ = ∫ dt ∫ dx ∫ dy ∫ dz = Δt · Δx · Δy · Δz. So this 4-volume is finite (for finite deltas). The above is stated explicitly in MTW p147, “Volume Integrals in Spacetime”. The same will be covered in any text such as tensor analysis that covers general curvilinear coordinates — look for things like √(det(g)) where g is the metric matrix, and depending on the context g will have a minus sign or not, such that the standard orientation gives a positive integral. Just as with integrals in Euclidean space, any spacetime integral can be integrated using the above by chopping up the integrand into rectilinear elements. But for dealing with spheres, the only sane thing to do is to use spherical coordinates. Embedding Euclidean Spheres in Euclidean SpaceFor our purposes, understanding the basics of embeddings, mappings, and metrics are essential. Embeddings are great aids in reasoning about geometries. Mappings are the general class to which embeddings belong. Metrics are the way geometries are defined intrinsically (without reference to an embedding), and in the case of orthogonal coordinates, which we will always use, the side lengths whose product gives the volume element can be read off from the metric Visualizations are another very helpful tool for understanding geometries. I’ll briefly touch on that the first time we have to consider a non-trivial higher dimensional space (Case 1). First, imagine an ordinary sphere in 3D Euclidean space, ie, a 2D surface embedded in E3. You could call the integral of the surface a “surface integral” and the integral of the embedding space enclosed by the surface a “volume integral”, but such names just confuse things in higher dimensions, so I’ll use the term “d-volume” regardless of d. Let’s first consider d-spheres in Euclidean space. First I’ll make a certain specific comparison to illustrate the main point, and then discuss the specifics in more general terms. Everything now is Euclidean. The equation of a 2D sphere, which can be viewed as embedded in 3D euclidean space E3, is (s2) x² + y² + z² = r² The equation of a 3D sphere, which can be viewed as embedded in 4D euclidean space E4, is (s3) u² + x² + y² + z² = r² Now using spherical coordinates let r denote the radial variable and w1, w2, … the angle variables. E.g., a point on the surface of a 2D sphere of radius r is given by (w1, w2), and on a 3D sphere by (w1,w2,w3). The surface of a sphere is covered by the range 0 to 2π for the single angle that appears only as its differential, and 0 to π for all others. 2-vol of the surface of a 2-sphere (ordinary 2D surface area)
= ∫∫ r² sinw1 dw1 dw2 = 4 π r² 3-vol of the E3 embedding space enclosed by a 2-sphere (ordinary 3D sphere volume)
= ∫∫∫ r² sinw1 dr dw1 dw2 = 4/3 π r³ 3-vol of the surface of a 3-sphere
= ∫∫∫ r³ sin²w1 sinw2 dw1 dw2 dw3 = 2 π² r³ 4-vol of the E4 embedding space enclosed by a 3-sphere
= ∫∫∫∫ r³ sin²w1 sinw2 dr dw1 dw2 dw3 = 1/2 π² r4 The main point I want to make here is that both (s2,3) and (s3,3) are 3-volumes, or triple integrals — yet they have different values. (s2,3) is an “extrinsic” 3-volume, since it involves the embedding space (ie not on the surface) (s3,3) is an “intrinsic” 3-volume (ie on the surface) Embeddings and MappingsNow some observations and language about the above. Above 3 dimensions, intuition inevitably starts to fail abruptly and precipitously, so the more ways one has to reason about geometries the better. The two integrals for s2, (s2,2) and (s2,3) (and likewise the two integrals for s3), differ by whether one integrates the surface or the embedding space enclosed by the surface, which in this case is whether dr is part of the volume element or r = fixed. The dimensionality of a volume element is how many coordinate differentials appear (eg, dr or not). [Footnote: The pairs of integrals also are related by differentiation / integration with respect to r. Integration/differentiation works only for fixed d-dim, it can’t change the dim (eg (s2,3) is not the derivative of (s3,3)). The reason for this is easy to see by looking at the formulas for the volume and surface of d-dim spheres given in Wolfram’s book Notes).] The transform equations for cartesian-spherical coords in E3 space are (TE3)
y = r sin w1 sin w2 z = r cos w1 The fact that the transform equations (TE3) define an embedding of a 2D sphere in E3 is shown by verifying that (s2) is satisfied by the transform variables, by squaring the RHS’s of the transform equations and finding that their sum equals r². Since an embedding increases the number of dimensions, then as an embedding the transform (TE3) is regarded as a mapping from 2 variables (w1,w2) to 3 variables (x,y,z). Given this view, r = fixed and dr = 0. Note that an embedding can increase the dimensionality by more than 1, e.g. a 1D curve in E3. An embedding is also called an immersion, or a subspace of the embedding space. An embedding is also a parametric representation. The coordinates of the embedded surface, before they are transformed to the embedding space, are the parameters of the parametric representation of the embedded surface. For example, the parameters of (s2) are w1 and w2, and the transforms (TE3) yield a parametric representation of (s2) in E3. Another example is a 1D curve in E3 where the curve is represented parametrically by the single parameter s and the transform equations that map s into x,y,z. We’ll use the term mapping to refer to transforms between any two sets of variables, with any number of variables or dimensions each. If the number of dimensions is regarded as different, we’ll usually call it an embedding. Rigorous definitions of mappings and embeddings involve various details (one-to-one, what to do with singular points, etc) but we won’t require that level of detail. The transform (TE3) may also be regarded as a mapping between 3 variables (r,w1,w2) and 3 variables (x,y,z). In this view, r is a variable so the differentials contain the dr terms. Thus, the presence of a dr in a geometry simply means that r is a variable, regardless of whether the geometry is arrived at via a mapping or an embedding. Don’t read too much into these ideas — they are only intended as aids in reasoning about geometries. MetricsMetrics are defined as quadratic forms in the differentials. In any orthogonal coords, the cross-terms vanish. The cartesian metric of E3 is: (E3c) ds² = dx² + dy² + dz² This metric in spherical coords can be found by taking differentials of the transform equations (TE3), with the dr terms included since we want the 3-space (r,w1,w2), and plugging into (E3c), yielding (E3s) ds² = dr² + r² (dw1² + sin²w1 dw2²) For our purposes, we’ll regard a metric, a coordinate system, a geometry, a space, and a surface as all synonymous. It’s useful to know that it’s not always easy to determine whether two metrics are equivalent. Even metrics for Euclidean space can very easily be made quite unrecognizable by nonlinear transforms. In fact, at least according to Wolfram’s book, above 4D the isometric equivalence problem is actually undecidable. Sometimes I find it useful to think in terms of degrees of freedom (dof).
A differential volume element is the product of the differential side lengths. For our orthogonal coord systems, side lengths may be simply read off from the metric as the square root of the coordinate differentials. For (E3c) this is just dV3 = (dx)(dy)(dz) For (E3s) the 3-volume element is that of (s2,3) dV3 = (dr)(r dw1)(r sinw1 dw2)
The CasesNow let’s look at 4D Minkowski space (M4) and your question re the “volume of a sphere in M4”. Case 1 seems closely related to your question, and its 4-volume is infinite. Then I point out a couple of ways that it could be modified to give cases with finite 4-volumes. Case 2 is a related possibility for which the 4-volume is finite. While Case 2 is not the 4-volume you ask about, I’m guessing that it is the source of your intuition that the volume should be finite. Case 3 completes and illuminates Cases 1 and 2. Cases 1 2 and 3 start by defining a (spatial) 3-surface, and add the fourth coordinate (time) independently to get the 4-volume. Case 4 starts with a 4-surface, and the first of the two sub-cases seems like the other most closely related possibility for interpreting your question. All four Cases also have physical relevance, which will be briefly described. I have calculated some but not all of the 4-volumes of the various cases. Again, my intention is primarily to shed light on why the possibilities are so numerous and how they relate to each other. Understanding this tutorial should enable you to calculate any integrals that interest you. Case 1Your questions are about the volume associated with the equation of the 3-surface (ps3) –u² + x² + y² + z² = r² which is closely related to the Euclidean 3-sphere (s3) u² + x² + y² + z² = r² The name (ps3) indicates “pseudo-sphere” (here a 3-surface). The term “pseudo” is used in the literature to refer to a space with exactly one dimension with opposite sign from the rest. Thus M4 space is also called pseudo-E4 (pE4 here) and the (ps3) space is called a pseudo-sphere. “Spherical” means “rotationally symmetric”, and can be made to include (ps3) via a more general definition of rotation, in which hyperbolic are allowed in addition to circular (ordinary trig) rotations. Re. relativity, Lorentz transforms are a certain hyperbolic rotation. It turns out that a 3-pseudo-sphere (ps3) cannot be embedded in E4.The reason for this is described below. At this point, intuitions begin to fail abruptly — in particular, don’t (try to) picture (ps3) as a hyperbolic surface in E4, because such a thing does not exist. However, (ps3) can be embedded in pE4 (M4), as a “hyperbolic surface in M4” — whatever that might look like. Re. “whatever that might look like”, visualizations are another helpful tool for understanding geometries. This is typically done by taking some kind projection or slice of the space that suppresses one or more dimensions. Animation is another possibility, as your article enjoyably demonstrates. Returning to the embedding of (ps3) in M4, the metric of M4 (pE4) is (M4c) ds² = –du² + dx² + dy² + dz² and in spherical coordinates of the “spatial” components, (M4s) ds² = –du² + dr² + r² (dw1² + sin²w1 dw2²) Note a) 4 coordinates (u,x,y,z) or (u,r,w1,w2) b) If one identifies u with t, this is the metric of “flat” spacetime, or special relativity, or Minkowski/Lorentz. One of the principles of general relativity is that the tangent spacetime at every event in spacetime is flat (M4). Just as any 2D spatial surface is everywhere locally Euclidean, spacetime is everywhere locally Lorentzian. Also, physical spacetime is a 4D surface that we are confined to deal with purely intrinsically, since we have no access to any supposed embedding space of it. c) In flat spacetime, space is flat
d) The hyperbolic nature of M4 thus necessarily involves the negative fourth component. This is reflected in the fact that Lorentz transformations are hyperbolic rotations with respect to velocities. For comparison, the metric for E4 is (E4c) ds² = du² + dx² + dy² + dz² (E4s) ds² = dr² + r² [dw1² + sin²w1 (dw2² + sin²w2 dw3³)] It is useful to note that (E4s) is dr² plus the metric of the 3-sphere, and that this relationship holds in general for the metrics of EN and (N-1)-sphere. Now, the metric of the 3-pseudo-sphere (ps3) is (ps3s) ds² = r² [dw1² + sinh²w1 (dw2² + sin2² dw3²)] Note a) Fixed r, 3 dof b) Differs from the 3-sphere part of (E4s) by the sinh(w1) instead of sin(w1). This will be shown to be the metric of a 3-hyperboloid (in M4) so the hyperbolic function is expected. The embedding of (ps3) in M4 is achieved by the transform equations (TM4)
y = r sinh w1 sin w2 sin w3 z = r sinh w1 cos w2 u = r cosh w1 The embedding of (ps3) in M4 by (TM4) is shown by taking the differentials of (TM4) — without dr’s since we’re regarding (TM4) as an embedding from 3 angles to 4 cartesians — and substituting into the metric (M4c) to obtain the metric (ps3s). Squaring the (TM4) equations yields
which shows that
is a (“two sheet”) 3-hyperboloid in M4. The reason (ps3) is not embeddable in E4 (or higher) is that as the “radial coordinate” w1 increases from 0 to inf, the circumference of the corresponding 2-spheres increase as sinh(w1). Since sinh(w1) > w1 for all w1, the circumferences increase faster than in fat space. Since (ps3) is a 3-surface, the question remains what “the volume of (ps3)” means. For this Case 1, I presume you’re thinking of the volume of the embedding space M4, enclosed by he surface of (ps3), in analogy with the embedding volume of E3 enclosed by the surface of a 2D Euclidean sphere. However,
First let’s examine the 3-volume of the entire surface (ps3)
= ∫∫∫ r³ sinh²w1 sin w2 dw1 dw2 dw3 = ∫∫ r³ sin w2 dw2 dw3 ∫ sinh²w1 dw1 = r² ∫[0,π]dw3 ∫[0,2π]dw2 ∫[0,inf]sinh²w1 dw1 and
The corresponding (spacetime) 4-volume
is therefore also infinite for any t. It’s not surprising that the 3-hyperbola given by equation (ps3) is unbounded and hence has infinite 3-volume. The equation doesn’t bound or limit the surface in exactly the same way that the 1D hyperbola curve y² – x² = r² doesn’t bound or limit the curve. Unlike the 1D circle, the equation doesn’t define a curve of finite length, nor does it enclose a finite region of E2. We have embedded (ps3) as a 3-hyperboloid in M4, ie we found the locus of points in M4 that satisfy (ps3), took the 3-integral over the region of M4 defined by (ps3), and added the fourth component independently to get the 4-volume. The crucial point is that the constraint (ps3) doesn’t restrict the surface from being unbounded. Comparing this integral to the finite volume 4-rectangle of M4 in the first section: A cube is a closed surface that encloses a region of its embedding space. A sphere is rotationally symmetric, and is open or closed depending on whether or not a hyperbolic rotation is involved. Case 1 Finite VariantsOne could alter the (ps3) geometry to have finite 3-volume in at least a couple different ways:
Global topological closure is fundamentally very different from selecting a portion of a surface. A global topology is required in addition to a metric to fully specify a space. The implicit or default specification of an open global topology that is presumed in the absence of an explicit specification is in reality an arbitrary choice. Physics4D geometries can be interpreted purely mathematically or also physically, by either regarding the fourth coordinate simply as an additional mathematical index or by identifying it with time. Cases 1 2 and 3 form a natural family in terms of both mathematics and physics (which is relativistic). Re. the latter, they are the 3 variants of the “isotropic and homogenous” cosmology, with constant spatial curvature. Case 1 is the open universe of negative constant curvature, Case 2 is the closed universe of positive constant curvature, and Case 3 is the flat universe that divides them. These 3 cosmologies are all of the “expanding universe” type, with the famous analogy of “pennies on a balloon”. The pennies represent objects of galactic scale which themselves do not expand (the length of a meter stick remains fixed within them), but the space between them expands as the balloon is blown up. The cosmology of Case 4 is described there. The spatial 3-surfaces of constant curvature are “hypersurfaces of homogeneity”, with one such surface for each moment of time. The full spacetime metrics for the three cases may be written with the same form
= -dt²
+ a²(t) [ dw1² + F²(dw2² + sin²w2 dw3²) ] where a(t) is the “relative expansion rate” that varies with t, and “STI” stands for “space-time isotropic” (isotropy implies homogeneity but not the converse), and ds² is the spatial component which is determined by the factor F,
F = w1 for zero constant curvature - Case 3 F = sin w1 for positive constant curvature –
Case 2 In each case, the 4-volume is
Thus the full spacetime metric of Case 1, with (ps3) 3-space, is given by
a(t) = r so that
Cases 1 2 and 3 are covered in most any book on general relativity, but MTW p725f is exceptionally clear. Case 4 is compactly described in MTW p745, and in wonderful detail in Rindler p185f. Case 2This is not the case you ask about, but I suspect your intuition of finite 4-volume was based on this case. This is like Case 1, but with the 3-surface having positive constant curvature instead of negative, and it is embeddable in E4 rather than M4. Instead of the Case 1 pseudo-sphere (ps3), the surface is a 3-sphere (s3) u² + x² + y² + z² = r² The metric of the 3-sphere is (s3s) ds² = r² [dw1² + sin²w1 (dw2² + sin²w2 dw3³)] The metric of E4 from above (E4c) ds² = du² + dx² + dy² + dz² The 3-surface (s3) is embeddable in E4 via (TE4)
y = r sin w1 sin w2 sin w3 z = r sin w1 cos w2 u = r cos w1 which differs from (TM4) of Case 1 by having all circular and no hyperbolic functions. The embedding is shown by differentiating (TE4) and plugging into (E4c) to obtain (s3s). Squaring (TE4) and plugging into (s3) yields r², showing that the surface (s3) embedded in E4 is a 3-sphere. The 3-volume of the 3-sphere is finite (for finite r), since this 3-surface is closed. It is (s3,3) from the first section
= ∫∫∫ (r dw1)(r sinw1 dw2)(r sinw1 sinw2 dw3) = ∫∫∫ r³ sin²w1 sinw2 dw1 dw2 dw3 = 2 π² r³ The 4-volume with this spatial 3-surface is
= 2 π² r³ t which is finite for finite r and t. Re. physics, the full spacetime metric
is obtained from our cosmological metric
= -dt²
+ a²(t) [dw1² + F² (dw2² + sin²w2 dw3²)] by the substitutions
a(t) = r Case 3This is the zero curvature case that completes the family with Cases 1 and 2 and is interesting in that it yields M4 itself as the 4-metric. The zero curvature 3-surface is simply E3 space (E3s) dr² + r²(dw1² + sin²w1 dw2²) The transform equations is the mapping (not embedding) between cartesian and spherical
x = r sin w1 cos w2 y = r sin w1 sin w2 z = r cos w1 which simply show that (E3s) is E3. The 3-volume of the entire surface is
= ∫∫∫ (r² sin w1 dw2 dw1) ∫[0,inf]dr = inf which is the integral of all of E3 space. Like Case 1 it is unbounded and hence infinite. The infinity comes from the [0, inf] range of the radial variable, r here and w1 in Case 1. Thus of Cases 1 2 and 3 only the positive curvature Case 2 has finite 3-volume of the entire 3-surface. The 4-volume with this 3-volume is the 4-volume of all of M4 V4 = V3 ∫ dt = inf which is infinite for any t. Re. physics, the spacetime metric for this case is that of M4 itself (M4s) dst² = -dt² + dr² + r²(dw2² + sin²w2 dw3²) (where the two angles end up being named w2 and w3) which is obtained from the cosmological metric (STI) dst² = -dt² + a²(t)[dw1² + F²(dw2² + sin²w2 dw3²)] by the substitutions
a(t) w1 = r As in Case 1, the 3-volume of the entire 3-surface is infinite. However, since cartesian coordinates are natural in flat space, the toroidal topological closure described above is done very easily here by matching boundaries to create the identifications x = x+Δx, y = y+Δy, z = z+Δz Thus the integral of the entire surface can thereby made finite, ∫∫∫ = Δx · Δy · Δz which is the same as the corresponding cube volume. Case 4In this case we begin with a 4D surface, embeddable in 5D, so that the entire 4-volume integral may be performed on the 4D surface. There are two cases, one with negative constant curvature and the other with positive constant curvature. Re. physics, these 4-surfaces are isometric to the de Sitter metric, with positive “cosmological constant” for the negative curvature case and negative cosmological constant for the positive curvature case. These cases are called the de Sitter and the anti-de Sitter universes (I think I may have seen the terms de Sitter / anti-de Sitter reversed in some of the literature). The de Sitter cosmology is covered in virtually any book on general relativity (although not necessarily under that name), but the embedding of each case is spelled out in Rindler in unusual detail. The first case is for a 4-pseudo-sphere, which has negative constant curvature,
The surface (ps4) is embeddable in M5 (or pE5)
The pseudo-sphere (ps4) seems like a natural possibility for the definition of a 4D-sphere in a space related to M4. I haven’t carried out the integral, but I would expect the 4-volume of this entire surface to be infinite, since (ps4) defines an unbounded surface in a directly analogous manner to Case 1. But such spaces are full of surprises… The second case is for a 4-pseudo-pseudo-sphere, which has positive constant curvature,
The surface (pps4) is embeddable in pseudo-M5 (or ppE5)
For the embedding transform equations, see Rindler. Again I haven’t carried out the integral, but I would expect the 4-volume of this entire surface to be finite. But this positive curvature case (pps4) is more remote than this negative curvature case (ps4) from the sphere equation you cite (just as the positive curvature Case 2 (s3) is more remote than the negative curvature Case 1 (ps3)). References MTW: Gravitation, by Charles Misner, Kip Thorne, and John Archibald Wheeler.
Rindler: Essential Relativity: Special, General, and Cosmological, by Wolfgang Rindler.
I own only a few introductory GR books in addition to the above. A First Course in General Relativity, by Bernard F. Schutz.
The Geometry of Spacetime: An Introduction to Special and General Relativity, by James J Callahan
|
Footnotes (clicking on (^), on the left, brings back to the text)
(^) I am indebted to Maricarmen Martinez, who helped me with the derivation of the formulas as well as with the Mathematica animation.
(^) Note that Euclidean, Galilean, and Minkowskian geometries are all different from each other.
(^) Unrealistic, but not unrealizable. A Euclidean 4D-cube is called a 4-hypercube, is known since antiquity, and has been utilized by computer scientists as one of possible structures for a network topology. See this added paragraph of the present text for a drawing of it.
(^) It should actually not disappear from view: we should be able to see its far wall from the inside, receding to infinity. I did not consider it necessary to depict that part of the animation, especially given the already large size of the GIF file.
(^) 4D-spheres are bounded in 4D-space by definition: there is a 4D-sphere that includes them, namely, their own self. It is their projections on any subspace that includes time as one of its dimensions that have the hyperbolic character, hence, appear unbounded in that subspace.
(^) The volume of the n-dimensional sphere of radius r in Euclidean space is given by the following formula:
V(n, r) = a r n
where a = (1 / (n/2)!) π (n/2) if n is even, and a = ((2 (n+1)/2) / n!!) π ((n-1)/2) if n is odd, where n!! is the product of the odd numbers less than or equal to n.
Einstein, Albert (1961). Relativity: the Special and the General Theory. Crown Trade Paperbacks: New York, 1961.
All graphs and plots on this page were made with Mathematica
v. 4.0.1.
Back to the Index of Topics in Physics
Back to the Index of Topics in Mathematics