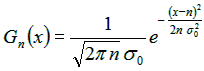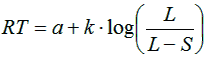Principle 1: Object Identification (Categorization)
In his influential “Six Easy Pieces”, Richard Feynman used the description “the Mother of all physics experiments” for the famous two-slit experiment,(1) because the results of many other experiments in quantum physics can be traced back to the observations in the two-slit experiment. Is there any such example in cognitive science that can serve as “the Mother of all cognitive problems”? Indeed, there is. Consider Figure 1.1:

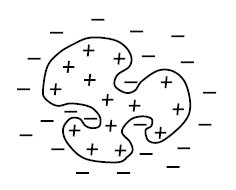
Figure 1.1. The most fundamental cognitive problem: what does this figure show?
The question in Figure 1.1 is: “What is depicted?” Most people would answer: “Two groups of dots.” (2) (3) It is possible of course to reply: “Just a bunch of dots”, but this would be an incomplete, a lazy fellow’s answer. What is it that makes people categorize the dots as belonging to two groups? It is their mutual distances, which, roughly, fall into two categories. Using a computer we can easily write a program that, after assigning x and y coordinates to each dot, will reach the same conclusion i.e., that there are two groups of dots in Figure 1.1. (4)
Why is this problem fundamental? Well, let us take a look at our surroundings: if we are in a room, we might see the walls, floor, ceiling, some furniture, this document, etc. Or, consider a more natural setting, as in Figure 1.2, where two “sun conures” are shown perching on a branch. Notice, however, that the retinas of our eyes only send individual “pixels”, or dots, to the visual cortex, in the back of our brain (see a rough approximation of this in Figure 1.3). How do we manage to see objects in a scene? Why don’t we see individual dots?
 |
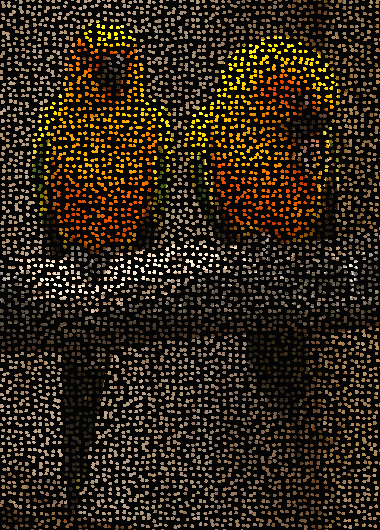 |
|
| Figure 1.2. Image of two sun conures (Aratinga solstitialis) perching on a branch | Figure 1.3. Conversion of previous image to “dots”, akin to retinal cells (an exaggeration; assume each dot is of one color) |
Figure 1.3 approximates the raw input we receive: each dot comes from a rod or cone (usually a cone) of the eye’s retina, and has a uniform “color” (hue, luminosity, and saturation).(5) The brain then “does something” with the dots, and as a result we see objects. What the brain does (among other things) is that it groups together the dots that “belong together”. For example, most dots that come from the chest of the birds in Figure 1.3 are yellowish, so they form one group (one region); dots from the belly of the birds are more orangy, so again they “belong together”, forming another region. Both yellow and orange dots are very different from the background gray–brown dots, so the latter form another region, or regions. How many regions will be formed depends on a parameter setting that determines when dots are “close enough” (both physically and in color) so that they are lumped together in the same group. In reality, visual object recognition is much more complex: the visual cortex includes edge detectors, motion detectors, neurons that respond to slopes and lengths, and a host of other special-purpose visual machinery that has been honed by evolution (e.g., see Thompson, 1993). But a first useful step toward object identification can be performed by means of solving the problem of grouping dots together. Notice that by solving the object identification problem we don’t perceive “two birds” in Figure 1.2 (that would be object recognition), but merely “there is something here, something else there,...” and so on.
Look again at Figure 1.1: in that figure, dots belong together and form two groups simply because they are physically close; that is, their “closeness” has a single feature: physical proximity, with two dimensions, x and y. But in Figure 1.3, dots belong together not only because of physical proximity, but also because of color; thus, in Figure 1.3 the closeness of dots depends on more features (more dimensions). If color itself is analyzed in three dimensions (hue, saturation, and luminosity) then we have a total of five dimensions for the closeness of dots in that figure. A real-world visual task includes a third dimension for physical proximity (depth, arising from comparing the small disparity of dots between the two slightly different images formed by each eye), and it might include motion as an additional feature that overrules others (“dots that move together belong together”). Thus, the “closeness of dots” is a multi-dimensional concept, even for the simplest visual task of object identification.
Now let’s consider a seemingly different problem (but which will turn out to be the same in essence). In our lives we perceive faces belonging to people from different parts of the world. Some are East Asian, others are African, Northern European, and so on. We see those faces not all at once, but in the course of decades. We keep seeing them in our personal encounters, and in magazines, TV programs, movies, computer screens, etc. During all these years we might form groups of faces, and even groups within groups. For example, within the “European” face, we might learn to discern some typically German, French, Italian faces, and so on, depending on our experience. Each group has a central element, a “prototype”, the most typical face that in our view belongs to it, and we can tell how distant from the prototype a given face of the group is. (Note that the prototype does not need to correspond to an existing face, it’s just an average.) This problem is not very different from the one in Figures 1.1 and 1.3: each dot corresponds to a face, and there is a large number of dimensions, each a measurable facial feature: color of skin, distances between eyes or between the eye-line and lips, length of lips, shape of nose, and a very large number of other characteristics. Thus, the facial space has a large dimensionality. We can imagine a central dot for each of the two groups in Figure 1.1, located at the barycenter (the center of gravity, or centroid) of the group, analogous to the prototypical face of a group of people. (And, again, the dot at the barycenter is imaginary, it doesn’t correspond to a real dot.) But there are some differences: contrary to Figure 1.1, faces are probably arranged in a Gaussian distribution around the prototypical face (Figure 1.4), and we perceive them sequentially in the course of our lifetimes, not all at once. Abstractly, however, the problem is the same.
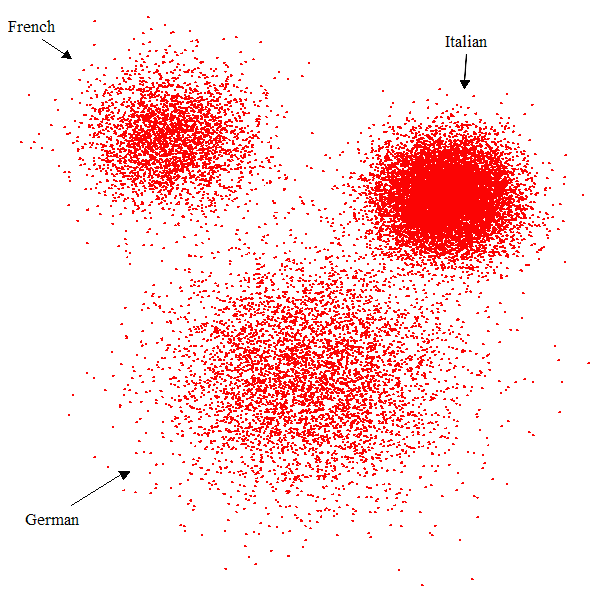
Figure 1.4. Abstract face space (pretending there are only two dimensions, x and y)
But vision is only one perceptual modality of human cognition. Just as we solve the problem of grouping faces and categorizing new ones as either belonging to known groups or becoming candidates for new groups, so we solve abstract group-formation problems such as categorizing people’s characters. We learn what a typical arrogant character is, a typical naïve one, and so on. The dimensions in this case are abstract personality features, such as greed–altruism, gullibility–skepticism, etc. Similarly, in the modality of audition we categorize musical tunes as classical, jazz, rock, country, etc.
In each of these examples (dots in Figure 1.1, pixels of objects, people’s faces, people’s characters, etc.), we are not consciously aware of the dimensions involved, but our subconscious cognitive machinery manages to perceive and process them. What kind of processing takes place with the perceptual dimensions is not precisely known yet, but the observed result of the processing has been summarized in a set of pithy formulas, known as the Generalized Context Model (GCM) (Nosofsky 1984; Kruschke, 1992; Nosofsky, 1992; Nosofsky and Palmeri, 1997). The GCM does not imply that the brain computes equations (see them in Figure 1.5) any more than Kepler’s laws imply that the planets solve differential equations while they orbit the Sun. Instead, like Kepler’s laws, the formulas of the GCM in Figure 1.5 should be regarded as an emergent property, an epiphenomenon of some deeper mechanism, the nature of which is unknown at present.
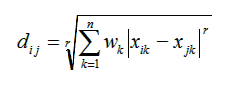 |
Equation 1 | |
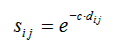 |
Equation 2 | |
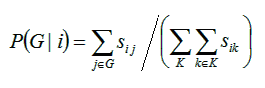 |
Equation 3 |
Figure 1.5. The formulas of the Generalized Context Model (GCM)
![]() The formula in Equation 1 gives the distance dij
between two “dots”, or “exemplars”, as they are more
formally called, each of which has n dimensions, and is
therefore a point in an n-dimensional space, or a so-called n-tuple
(x1,x2,...,xn). For example, each dot in Figure 1.1
is a point in 2-dimensional space. The wk’s are
called the weights of the dimensions, because they
determine how important dimension k is in calculating
the distance. For instance, if some of the dots in Figures 1.1 or
1.3 move in unison, we’d like to give a very high value to the
wk of the k-th dimension “motion with a given
speed along a certain direction” (this actually would comprise
not one but several dimensions); that’s because the common
motion of some dots would signify that they belong to the same
moving object, and all other dimensions (e.g., of physical
proximity) would be much less important. Normally there is the
constraint that the sum of all wk must equal 1. Finally, the r is often taken to
be equal to 2, which turns Equation 1 to a “weighted Euclidean
distance”.
The formula in Equation 1 gives the distance dij
between two “dots”, or “exemplars”, as they are more
formally called, each of which has n dimensions, and is
therefore a point in an n-dimensional space, or a so-called n-tuple
(x1,x2,...,xn). For example, each dot in Figure 1.1
is a point in 2-dimensional space. The wk’s are
called the weights of the dimensions, because they
determine how important dimension k is in calculating
the distance. For instance, if some of the dots in Figures 1.1 or
1.3 move in unison, we’d like to give a very high value to the
wk of the k-th dimension “motion with a given
speed along a certain direction” (this actually would comprise
not one but several dimensions); that’s because the common
motion of some dots would signify that they belong to the same
moving object, and all other dimensions (e.g., of physical
proximity) would be much less important. Normally there is the
constraint that the sum of all wk must equal 1. Finally, the r is often taken to
be equal to 2, which turns Equation 1 to a “weighted Euclidean
distance”.
![]() Equation 2 gives the similarity sij
between two points i and j (or “dots”, or
“exemplars”). If the difference dij
is very large, then this formula makes their similarity to be
nearly 0; whereas if the difference is exactly 0, then the
similarity is exactly 1. The c in the formula is a
constant, the effect of which is that if its value is high, then
attention is paid to only very close similarity, and thus many
groups (categories) are formed; whereas if its value is low, the
effect is the opposite: fewer groups (categories) are formed. (How
groups are formed is determined by Equation 3, see below.) Note
that in some versions of the GCM, the quantity c·dij
is raised to a power q, so that if q=1 (as in
Equation 2) we have an exponential decay function, whereas if q=2
we have a Gaussian decay.
Equation 2 gives the similarity sij
between two points i and j (or “dots”, or
“exemplars”). If the difference dij
is very large, then this formula makes their similarity to be
nearly 0; whereas if the difference is exactly 0, then the
similarity is exactly 1. The c in the formula is a
constant, the effect of which is that if its value is high, then
attention is paid to only very close similarity, and thus many
groups (categories) are formed; whereas if its value is low, the
effect is the opposite: fewer groups (categories) are formed. (How
groups are formed is determined by Equation 3, see below.) Note
that in some versions of the GCM, the quantity c·dij
is raised to a power q, so that if q=1 (as in
Equation 2) we have an exponential decay function, whereas if q=2
we have a Gaussian decay.
![]() Finally, Equation 3 gives the probability P(G |
i) that point i will be placed in group G.
The symbol K stands for “any group”, so the first
summation in the double-summation formula of the denominator says
“sum for each group”. Thus, suppose that some groups have
already been formed, as in Figure 1.4, and a new point (dot)
arrives in the input (a new European face is observed, in the
context of the example of Figure 1.4). How can we decide in which
group to place it? Answer: we compute the probability P(G
| i) for i = 1, 2, and 3 (because we have
3 groups) from this equation, and place it in the group with the
highest probability. An allowance must be made for the case in
which the highest probability turns out to be too low — lower
than a given threshold. In that case we can create a new group.
In practice, Equation 3 is computationally very expensive, so
some other heuristic methods can be adopted when the GCM is
implemented in a computer.
Finally, Equation 3 gives the probability P(G |
i) that point i will be placed in group G.
The symbol K stands for “any group”, so the first
summation in the double-summation formula of the denominator says
“sum for each group”. Thus, suppose that some groups have
already been formed, as in Figure 1.4, and a new point (dot)
arrives in the input (a new European face is observed, in the
context of the example of Figure 1.4). How can we decide in which
group to place it? Answer: we compute the probability P(G
| i) for i = 1, 2, and 3 (because we have
3 groups) from this equation, and place it in the group with the
highest probability. An allowance must be made for the case in
which the highest probability turns out to be too low — lower
than a given threshold. In that case we can create a new group.
In practice, Equation 3 is computationally very expensive, so
some other heuristic methods can be adopted when the GCM is
implemented in a computer.
A question arising from Equation 3 is how we determine the very initial groupings, when there are no groups formed yet, and thus K is zero. One possible answer is that we entertain a few different grouping possibilities, allowing the reinforcement of some groups as new data arrive, and the fading of other groups in which no (or few) data points are assigned, until there is a fairly clear picture of which groups are the actual ones that emerge from the data (Foundalis and Martínez, 2007).
What’s nice about the GCM equations is that they were not imagined arbitrarily by some clever computer scientist, but were derived experimentally by psychologists who tested human subjects, and measured under controlled laboratory conditions the ways in which people form categories. Experimental observations provide strong support for the correctness of the GCM, according to Murphy (2002).
What the above formulas do not tell us is how to decide what constitutes a dimension of a “dot”. For example: you see a face; how do you know that the distance between the eyes is a dimension, whereas the distance between the tip of the nose and the tip of an eyebrow is not? Now, we people do not have to solve this problem, because our subconscious cognitive machinery solves it automatically for us, in an as yet unknown way; but when we want to solve the problem of “categorization of any arbitrary input” in a computer we are confronted with the question of what the dimensions are. There is a method, known as “multidimensional scaling”, which allows the determination of dimensions, under certain conditions.(6) But more research is currently needed on this problem, and definitive answers have not arisen yet.
Opinions differ on which theory is best suited to describe the GCM. The question is: if categories are formed and look like those in Figure 1.4, then how are they represented in the human mind? This is the source of the well-known “prototype” vs. “exemplar” theory contention (see Murphy, 2002, for an introduction). The prototype theory says that categories are represented through an average value (but see Foundalis, 2006, for a more sophisticated statistical approach). The exemplar theory says that categories are represented by storing their individual examples. Many laboratory tests of the GCM with human subjects appear to support the exemplar theory, although no consensus has been reached yet. However, although the architecture of the brain seems well-suited for computing the GCM according to the exemplar theory, the architecture of present-day computers is ill-suited for this task. In Phaeaco (Foundalis, 2006), an alternative is proposed, which uses the exemplar theory as long as the category remains poor in examples (and thus the computational burden is low), and gradually shifts to the prototype theory as the category becomes more robust and its statistics more reliable. Whatever the internal representation of a category in the human mind is, the important observation is that the GCM formulas capture our experimental data of people’s behavior when they form categories.
The reader probably noticed that this section started with the question of object identification, and ended up with the problem of category formation. How was this change of subject allowed to happen? But the beauty of the First Principle is that it unifies the two notions into one: object identification and category formation are actually the same problem. It is tempting to surmise that the spectrum that starts with object identification and ends with abstract category formation has an evolutionary basis, in which cognitively simpler animals reached only the “lower” end of this spectrum (concrete object identification), whereas as they evolved to cognitively more complex creatures they were able to solve more abstract categorization problems.
The power of the First Principle is that it allows cognition to happen in a very essential way: without object identification we would be unable to perceive anything at all. Our entire cognitive edifice is based on the premise that there are objects out there (the nouns of languages), which we can count: one object, two objects... Based on the existence of objects, we note their properties (a red object, a moving object, ...), their relations (two colliding objects, one object underneath another one, ...), properties of their relations (a slowly moving object, a boringly uniform object, ...), and so on. Subtract objects from the picture, and nothing remains — cognition vanishes entirely.
A related interesting question is whether there are really no objects in the world, and our cognition simply concocts them, as some philosophers have claimed (e.g., Smith, 1996). But I think this view puts the cart in front of the horse: it is because the world is structured in some particular ways (forming conglomerations of like units) that it affords cognition, i.e., it affords the evolution of creatures that took advantage of the fact that objects exist, and used this to increase their chances of survival. Cognition mirrors the structure and properties of the world. “Strict constructivism” — the philosophical view that denies the existence of objects outside an observer’s mind — cannot explain the origin of cognition.